5. Дискретное преобразование Лапласса. Его свойства. Нахождение обратного преобразования. Понятие дискретной передаточной функции.

Дискретное преобразование

Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

(15.25)

Для смещенных решетчатых функций может быть записано аналогичное выражение:

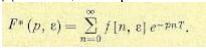(15.26)

Формулы (15.25) и (15.26) можно представить в символической записи:

В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина р = с + jw, где с — абсцисса абсолютной сходимости. Если с <∞, то ряд, определяемый формулами (15.25) и (15.26), сходится и решетчатой функции соответствует некоторое изображение. Как следует из (1:5.25) и (15.26), изображение решетчатой функции является функцией величины е^рТ. Для смещенных решетчатых функций в изображение будет входить, кроме того, параметр ε.

Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него. Применительно к z-преобразованию ниже будут рассмотрены основные свойства и теоремы дискретного преобразования Лапласа. Под z-преобразованием понимается изображение несмещенной или смещенной решетчатых функций, определяемое формулами:

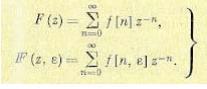
(15.29)

В этих формулах введено новое обозначение z= е^рТ. Из них следует, что z-преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только обозначением аргумента изображения.

Свойства

1. Свойство линейности. Это свойство заключается в том, что изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений. Пусть решетчатая функция определяется выражением

(15-46)

Тогда для ее изображения можно записать

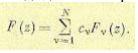
(15-47)

2. Теорема запаздывания и упреждения. Рассмотрим решетчатую функцию f[n — m], сдвинутую вправо (запаздывающую) на целое число тактов m. Тогда из формулы (15.29) следует, если обозначить n — m = r,

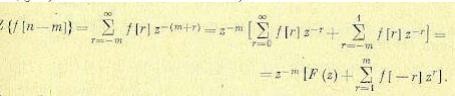
(15.48)

Здесь F(z) — изображение функции f[n]. Если исходная решетчатая функция f[n] равна нулю при отрицательных значениях аргумента, то формула (15.48) упрощается:

(15.49)

Если сдвиг функции f[n] происходит влево (упреждение) и рассматривается функция f[n+m] , где m— целое положительное число, то аналогично случаю запаздывания можно показать, что

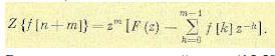
(15.50)

Второе слагаемое в правой части (15.50) обращается в нуль, если f[n] = 0 при n = 0, 1, . . ., m-1. При запаздывании на не целое число периодов m + ξ приходится вводить смещенную решетчатую функцию. Пусть рассматривается функция f[n -ε − m − ξ ], где m— целая, а ξ — дробная часть запаздывания. Если смещение е удовлетворяет условию 0 ≤ ε < ξ и f [n + ε − m − ξ ] = 0 при n + ξ < ξ + m при, то можно показать, что

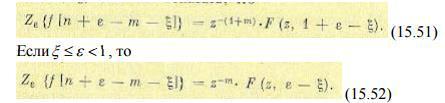
3. Теорема об умножении оригинала на экспоненту (теорема смещения в области изображений). Умножим решетчатую функцию на экспоненту е^λ nТ . Тогда из формулы (15.29) следует:

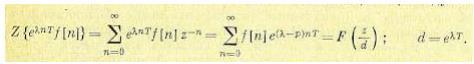
(15.53)

Для смещенной решетчатой функции аналогичная формула имеет вид

(15.54)

4.Теорема об умножении оригинала на степенную функцию. Пусть решетчатой функции f[n] соответствует изображение F(z). Тогда можно показать, что:

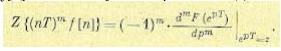
(15-55)

Для смещенной решетчатой функции аналогичная зависимость имеет вид

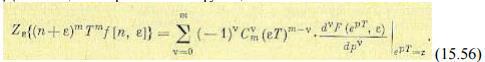
Обратное дискретное преобразование Лапласа

Понятие дискретной передаточной функции

Можно ввести понятие идеального импульсного элемента и иначе, считая, что он генерирует с периодом Т последовательность бесконечно коротких импульсов типа δ - функции, площадь которых пропорциональна сигналу ошибки х(t) в моменты времени t = nТ, т. е.

(15.116)

где δ т (t) = δ (t— nТ).

Представление импульсного элемента согласно (15.116) не соответствует действительности, так как никакой импульсный элемент не может генерировать бесконечные по высоте импульсы. Однако подобное формальное представление позволяет упростить изображение структурной схемы импульсной системы и поэтому используется. Введем понятие приведенной весовой функции wп(t) разомкнутого канала регулирования (рис. 15.11), понимая под этим термином реакцию непрерывной части системы совместно с экстраполятором на единичную импульсную решетчатую функцию х*[n] = δ 0 [n], которая определена формулой (15.32). При этом используется понятие идеального импульсного элемента в соответствии с (15.115), т. е. у* [n] = х [n]. Более строго весовую функцию wп (t) следует определить (см. главу 4) как отношение выходного сигнала у(t), возникающего при поступлении на вход экстраполятора единственной дискреты х0 в момент n = 0, т. е. функции х* [n] = х0 δ 0 [n], к значению х0:

(15.117)

Если выходную величину рассматривать только в дискретные моменты времени t= nТ или t = (n +ε ) Т, то разомкнутый канал регулирования будет представлять собой импульсный фильтр. Он может характеризоваться решетчатой весовой функцией wп[n] или wп [n, ε ], полученной из производящей функции wп (t). Заметим, что приведенная весовая функция отличается от обычной весовой функции непрерывного фильтра как своим видом, так и размерностью. Приведенная весовая функция содержит дополнительный множитель, имеющий размерность времени. Знание решетчатой весовой функции wп[n] или wп [n, ε ] позволяет найти реакцию импульсного фильтра на входную величину х [n] произвольного вида. Очевидно, что реакция импульсного фильтра на дискрету х [0] будет wп (t) х [0], реакция на дискрету х [1] будет wп (t — Т) х [1], реакция на дискрету х [m] будет wп (t- mТ) х [m]. Поэтому

где дискретная передаточная функция W(z) есть z-преобразование от приведенной решетчатой весовой функции:

(15.121)