9. Исследование устойчивости импульсных систем. Алгебраические критерии устойчивости.

Линейная импульсная САУ считается устойчивой, если после кратковременного внешнего воздействия (например, xвх(t)=δ(t)) при t стремящимся к бесконечности X (вых) стремящем к нулю.

Пусть – передаточная функция замкнутой системы:

(19.1)

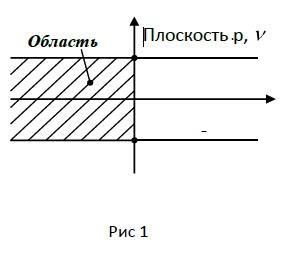
Корни характеристического уравнения рассматриваются в полосе

(рис 1), т.к. изображения периодичны по мнимой оси.

Если корни характеристического уравнения имеют отрицательные вещественные части, то система устойчива.

Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть – система неустойчива.

Если один или несколько корней характеристического уравнения расположены на мнимой оси, то импульсная система нейтральна.

Уравнение (19.1) является трансцендентным, поэтому сделаем в характеристическом уравнении A*(p) = 0 подстановку e pT = z. (19.2)

Тогда получим A(z) = a0zn+ a1zn-1 +…+ an =0.(19.3)

Для устойчивости системы корни уравнения (19.3) должны находиться внутри окружности единичного радиуса.

Алгебраический критерий устойчивости (аналог критерия Гурвица)

Характеристическое уравнение замкнутой импульсной системы:

A*(p) = C*(p)+ B*(p)=a0enpT+ a1e(n-1)pT+…+ an =0. (19.4)

Сделаем подстановку e pT = z, тогда получим:

A(z) = a0zn+ a1zn-1 +…+ an =0. (19.5)

Так как подстановка преобразует полуполосу во внутренность круга единичного радиуса (рис 1) , то применительно плоскости z необходимое и достаточное условие устойчивости формулируется следующим образом: замкнутая импульсная система устойчива, если все

корни А(z) лежат внутри круга единичного радиуса, т.е. все нули А(z) по модулю меньше единицы.

Чтобы привести условия устойчивости импульсной системы к аналогичным условиям устойчивости Гурвица для непрерывных систем в A(z) произведем замену переменных (19.6),

Откуда следует (19.7)

Из (19.7) видно, что если вещественная часть комплекса vi = αv +jβv будет отрицательна, то |zi| < 1 и система устойчива.

Характеристическое уравнение принимает вид

(19.8)

или после преобразования:

(19.9),

Где – новые коэффициенты.

Так как подстановка (19.6) преобразует круг единичного радиуса в комплексной плоскости z (рис 2) в левую полуплоскость (рис 1), то условие устойчивости импульсной системы формулируется так: замкнутая импульсная система устойчива, если корни А(v) лежат в левой полуплоскости т.е. выполняются условия Гурвица (при выполнении необходимого условия устойчивости (положительность всех коэффициентов характеристического уравнения) должны быть положительны n главных определителей матрицы Гурвица)

10. Исследование устойчивости импульсных систем. Частотные критерии устойчивости.

Вопрос исследования устойчивости импульсных систем рассмотрен в пункте выше (29 вопрос)

Критерий устойчивости Михайлова для импульсных систем

Пусть имеем характеристический полином замкнутой системы:

A(z) = a0zn+ a1zn-1 +…+ an (19.9), где z = epT.

Разложим (19.9) на сомножители: A(z) = a0(z –z1)(z –z2)…(z –zn), (19.10)

где zi – корни уравнения A(z)=0, соответствующие корням pi

характеристического уравнения A*(p)=0.

Положим z = ejωT и найдем изменение аргумента (фазовый сдвиг) одного из сомножителей (z –zi), входящих в состав A(z), Δarg (ejωT -zi) при изменении

A*(jω) = a0enjωT+ a1e(n-1) jωT+…+ an = X(ω)+j Y(ω).

Если изменять ω от 0 до ωи/2 и учесть, что число сомножителей (z –zi) равно степени характеристического уравнения n, то критерий можно сформулировать следующим образом.

Для того чтобы импульсная система была устойчива, необходимо и достаточно, чтобы годограф A*(jω) с ростом от 0 до обходил последовательно в положительном направлении 2n квадрантов (то есть вектор поворачивался на угол nπ при изменении ω от 0 до ωи/2).

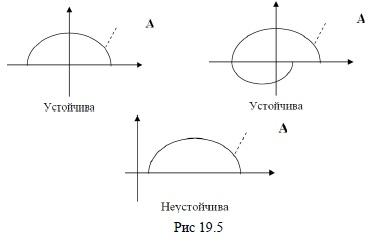
На рис. 19.5 приведены варианты годографа Михайлова для систем первого и второго порядка и сделаны выводы об устойчивости систем.

Критерий устойчивости Найквиста для импульсных систем

Пусть разомкнутая система устойчива или нейтральна и имеет передаточную функцию Wp*(p).

Если разомкнутая импульсная система устойчива (т.е. устойчива линейная часть системы), то замкнутая импульсная система регулирования устойчива, если годограф частотной характеристики разомкнутой системы при изменении ω от 0 до π не охватывает точку (-1, j0).

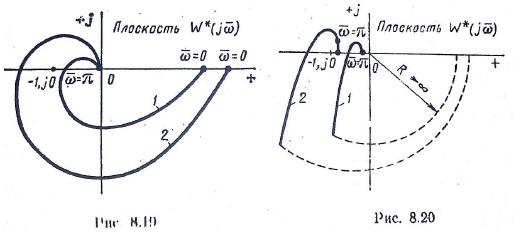
На рис. 8.19 изображены годографы W(p),

Если разомкнутая импульсная система неустойчива, т.е. если передаточная функция линейной части имеет r полюсов с положительной вещественной частью, то замкнутая система импульсного регулирования будет устойчива, если годограф * W(p) частотной характеристики разомкнутой системы охватывает точку (-1, j0) в положительном направлении r/2 раз.

Если разомкнутая система нейтральна, т.е. если передаточная функция содержит r полюсов, равных нулю, то импульсная система будет устойчива, если годограф W p , дополненный дугой бесконечно большого радиуса, соответствующей углу – r π/2, не охватывает точку (-1, j0).

На рисунке 8.20 кривая 1 соответствует устойчивой, а кривая 2 – неустойчивой замкнутой системе.