Высшая математика - часть 1 [технические специальности] 1-курс КР-1 в-1

Вариант 1

Задача 1. Даны четыре вектора a (а1, а2, а3), b (b1, b2, b3), c (c1, c2, c3) и d (d1, d2, d3) в

некотором базисе. Показать, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.

a (4,5,2), b (3, 0, 1), c (-1, 4,2), d (5,7,8).

Решение.

Составим и вычислим определитель, столбцами которого являются координаты векторов

a , b , c :
D =		4	3	-1			= 4 ×(0 - 4)- 3× (10 - 8)-1×(5 - 0) = -27 ¹ 0 , следовательно, эти векторы
		5	0	4
		2	1	2

являются базисом в трехмерном пространстве R3 .																						= Di ,i =
Решаем систему d = x a + x																		b + x		c методом Крамера: x
																	2		3		i							1,3, где
																1							D
D		=		5					3	-1						= 5 ×(0 - 4) - 3× (14 - 32) -1× (7 - 0) = 27 Þ x							=	27			= -1,
	1			7					0	4
																						1	- 27
				8					1	2
D2		=						4	5	-1						= 4 × (14 - 32) - 5× (10 - 8) -1×(40 -14) = -108 Þ x2 =													-108		= 4 ,
								5	7	4
								2	8	2																	- 27
D3		=				4			3	5		= 4 × (0 - 7) - 3× (40 -14) + 5 ×(5 - 0) = -81 Þ x3											=		- 81		= 3 .
						5			0	7
						2			1	8													- 27

Итак, d = -a + 4b + 3c .

Задача 11. Даны координаты вершин пирамиды A1A2A3A4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объём пирамиды; 6) уравнения прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертёж.

А1(3,1,4), А2(-1,6,1), А3(-1,1,6), А4(0,4,-1).

Решение.

Векторы:

A1 A2 = (-1- 3;6 -1;1- 4) = (- 4;5;-3),

A1 A3 = (-1- 3;1-1;6 - 4) = (- 4;0;2),

A1 A4 = (0 - 3;4 -1;-1- 4) = (- 3;3;-5).

1) Длина ребра: | A1 A2 |= 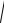(- 4)2 + 52 + (- 3)2 = 52 .

2) Вычисляем: cosÐA2 A1 A4

=

A1 A2 × A1 A4

=

12 +15 +15

=

42

Þ

| A1 A2 | × | A1 A4 |

×

(- 3)2 + 32 + (- 5)2

5 86

5

2

1

Þ ÐA A A = arccos				42		» 0,438 (рад.).
2	1	4	5	86
7) Уравнение плоскости A1 A2 A3 :
							x - xA	y - yA
							xB - xA	yB - yA
							xC - xA	yC - yA

z - zA

zB - zA = 0 zC - zA

																							x - 3				y -1 z - 4
																							- 4				5			- 3				= 0
																							- 4				0			2
													(x - 3)× (10 + 0)- (y -1)× (- 8 -12)+ (z - 4)×(0 + 20) = 0
																								x + 2y + 2z −13 = 0
	Нормаль плоскости A1 A2 A3 : n(1;2;2).
	3) Вычисляем:
	sin ϕ =					cos(90o			-ϕ)				=				n × A1 A4					=								- 3 + 6 -10											=	7			Þ
									7						| n | × | A1 A4 |											12 + 22 + 22					× (- 3)2 + 32 + (- 5)2											3 43
	Þ ϕ = arcsin
													» 0,364 (рад.).
							3		43
	4) Площадь грани A1 A2 A3 :
		1												1				i		j			k				10
	S =		×	A A ´ A A									=			× |		- 4 5 - 3							|=			×	i + 2 j + 2k						= 5			1+ 4 + 4	= 15 (кв.ед.).
	2				1		2		1		3		2														2
																		- 4	0			2

5) Объем пирамиды:

V = 16 × A1 A2 A1 A3 A1 A4

6) Уравнения прямой

8) Уравнения высоты

Строим чертеж:

		1			- 3	3			- 5											10								- 3 + 2 ×3 + 2 ×(- 5)																	35
	=		× |		- 4	5			- 3						|=									×																				=		(куб.ед.).
	6				- 4	0			2											6																									3
	A1 A2 :					x - x1															y - y1															z - z1
													=																			=
						x		2	- x											y			2	- y												z	2		- z
									1																1														1
										x - 3							=						y -1							=				z - 4
										- 4													5											- 3
	A4 H ^ A1 A2 A3 :
								x - x4								=					y - y4											=			z - z4
										n													n
																									2												n		3
									1
											x		=					y - 4								=							z +1
									1											2												2

2

Задача 21. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон x+y-1=0 и y+1=0, если известно, что диагонали параллелограмма пересекаются в точке P(-1,0).

Решение.

Координаты точки B - точки пересечения данных прямых – находим из системы:

ìx + y -1 = 0			ìx -1-1 = 0	ìx = 2
í		Û í		Û í
îy +1 = 0			îy = -1	îy = -1
Итак: B(2;-1).
Координаты точки D ( BD - диагональ параллелограмма) находим исходя из того, что P -
середина BD :			xD = 2xP - xB = -2 - 2 = -4 , yD = 2yP - yB = 0 +1 = 1.
Т.о.,	D(- 4;1).

Уравнение стороны AD , параллельной прямой y +1 = 0 (наклонный коэффициент этих прямых kAD = kBC = 0):

		y - yD = kAD (x - xD )
					y −1 = 0
Координаты точки A находим из системы:
ìx + y -1 = 0	ìx +1-1 = 0	ìx = 0
í	Û í	Û í
îy -1 = 0	îy = 1	îy = 1
Итак: A(0;1).
Искомое уравнение диагонали AC :				x - xA			=		y - yA
				xP - xA					yP - yA
					x	=		y -1
					-1			0 -1

y = x +1

Ответ. y = x +1.

3

Задача 31. Построить на плоскости область решений системы линейных неравенств.

Решение.

Сначала строим соответствующие прямые, а затем выбираем необходимую полуплоскость (для первых двух прямых – та, в которой лежит точка (0;0), а для третьей – та, в которое не лежит точка (0;0)). Пересечение полученных полуплоскостей – искомая область.

Задача 41. Составить уравнение линии, каждая точка которой равноудалена от точки A(2,2) и от оси абсцисс.

Решение.

Пусть M (x; y) - произвольная точка данной линии, тогда по условию:

(x − 2)2 + (y − 2)2 =| y | .

Возведем в квадрат обе части уравнения:

(x − 2)2 + (y − 2)2 = y2 (x − 2)2 + y2 − 4y + 4 = y2 (x − 2)2 = 4(y −1)

Данная линия – парабола.

Ответ. (x − 2)2 = 4(y −1).

4

Список использованных источников

1.Власов В.Г. Конспект лекций по высшей математике. - М.: Айрис, 1996.

2.Высшая математика: Общий курс: Учебник / А-В.Кузнецов, Л-Ф-Янчук, С.А.Мызгаева и др.; Под общей редакцией профессора А.И.Яблонского. - Мн.:

Выш. шк., 1993.

3.Дадаян А.А., Дударенко В.А. Алгебра и геометрия: Учеб. пособ. - Мн.: Выш. шк., 1989.

4.Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учеб. пособ. для вузов - М: Наука, 1989.

5