
К.р. №5-6 1 вариант
.doc221. Найти общее решение дифференциального уравнения первого порядка:
![]()
Решение.

 ,
сделаем замену:
,
сделаем замену:
![]() .
.
Тогда
![]() ,
,
![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() - общее решение.
- общее решение.
“Потерянные”
решения:
![]()
![]()

![]()
![]()
![]()
![]() ОДЗ(область
допустимых значений) уравнения
ОДЗ(область
допустимых значений) уравнения
![]()
![]()
![]() -
решение получится и ОР при
-
решение получится и ОР при
![]() .
.
Ответ:
![]() ,
,
![]()
231. Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям:
![]()
Решение.
1)
![]()
![]() -
характеристическое уравнение
-
характеристическое уравнение
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() - ОР (*)
- ОР (*)
2)
Правая часть
![]()
2.1)
![]() (**)
(**)
![]() -
вид частного решения (**)
-
вид частного решения (**)
![]() ,
,
![]() .
Подставим в (**):
.
Подставим в (**):
![]()


![]() -
вид ЧР(**)
-
вид ЧР(**)
2.2)
![]() (***)
(***)
![]()
![]() ,
,
![]() .
Подставим
в (***):
.
Подставим
в (***):
![]()


![]() -
ЧР
(***)
-
ЧР
(***)
Общее решение ДУ:
![]()
![]() ,
,
![]() .
.
3)
 ;
;
![]()
 ;
; 
Частное решение ДУ, удовлетворяющее начальным условиям, имеет вид:
![]()
Ответ:
![]()
241. Найти общее решение системы уравнений:

Решение:
Применим метод Эйлера. Запишем систему в матричной форме:
 .
.
Составляем характеристическое уравнение системы:

![]()
![]()
![]() ,
,
![]()
1)
![]()
![]()
![]() ,
,
![]() ,
где
,
где


![]()
 ,
,
![]()
2)
![]()
![]()
![]() ,
,
![]() , где
, где


![]()
![]() ,
,
![]()
3) Общее решение системы ДУ находим, как линейную комбинацию полученных частных решений, т.е.
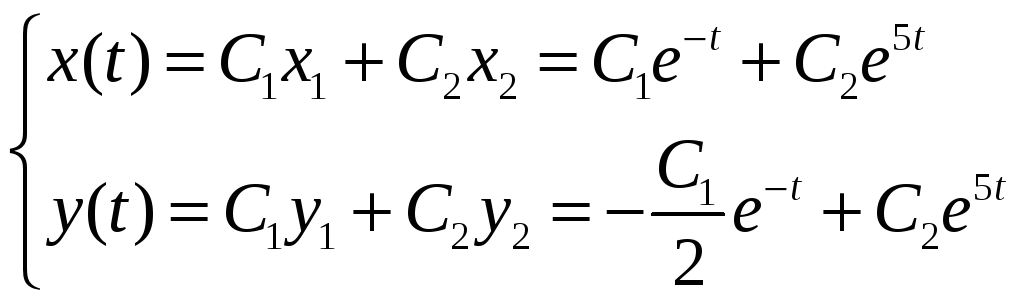 ,
где
,
где
![]() ,
,
или в матричной форме
 .
.
Ответ:
 ,
где
,
где
![]()
251.
Скорость распада радия пропорциональна
его наличному количеству
![]() .
Найти зависимость
.
Найти зависимость
![]() от времени
от времени
![]() ,
если известно, что по истечении 1600 лет
остается половина первоначального
количества радия. Принять первоначальное
количество радия
,
если известно, что по истечении 1600 лет
остается половина первоначального
количества радия. Принять первоначальное
количество радия
![]() .
.
Решение:
![]() -
количество радия в момент времени
-
количество радия в момент времени
![]()
![]() ;
;
![]()
1)
(*)
![]() - условие пропорциональности
- условие пропорциональности
![]() и
и
![]() .
.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() - ОР(*)
- ОР(*)
2)
![]()
![]()
![]()
![]()
3)
![]()
![]()
![]()
![]()
Ответ:
![]()
261. Вычислить криволинейный интеграл
![]()
вдоль
линии
![]() от точки А (–1;1) до точки В (2;2).
от точки А (–1;1) до точки В (2;2).
Решение:

![]()
1)
Отрезок
![]() задан уравнением:
задан уравнением:
![]()
![]()
![]() .
.
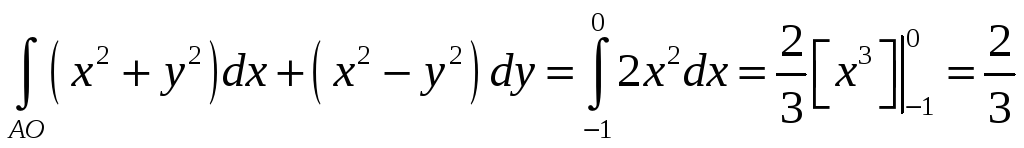 .
.
2)
Отрезок
![]() задан уравнением:
задан уравнением:
![]()
![]()
![]() .
.
 .
.
3)
 .
.
Ответ: 6.
271.
Вычислить с помощью тройного интеграла
объем тела, ограниченного указанными
поверхностями. Данное тело и его проекцию
на плоскость
![]() изобразить на чертежах:
изобразить на чертежах:
![]()
Решение:


![]() -
тело ограниченное
-
тело ограниченное
![]() .
.
![]() -
проекция
-
проекция
![]() на плоскость
на плоскость
![]() .
.
Вычислим
объем
![]() :
:


![]() (куб.ед.)
(куб.ед.)
Ответ:
![]() куб.ед.
куб.ед.
281.
Вычислить с помощью двойного интеграла
в полярных координатах площадь фигуры,
ограниченной кривой, заданной уравнением
в декартовых координатах. Параметр
![]() положителен.
положителен.
![]()
Решение:
![]() ,
,
![]() .
.
![]()

Перейдем к полярным координатам:
 ,
тогда
,
тогда
![]()
![]()
![]()
![]()
![]()
![]()

 .
.
 (кв.ед.)
(кв.ед.)
Ответ:
![]() кв.ед.
кв.ед.
291.
Даны векторное поле
![]() и плоскость
и плоскость
![]() :
:
![]() ,
которая совместно с координатными
плоскостями образует пирамиду
,
которая совместно с координатными
плоскостями образует пирамиду
![]() .
Требуется вычислить: 1) поток векторного
поля
.
Требуется вычислить: 1) поток векторного
поля
![]() через часть плоскости
через часть плоскости
![]() ,
ограниченной координатными плоскостями,
в том направлении нормали к плоскости
,
ограниченной координатными плоскостями,
в том направлении нормали к плоскости
![]() ,
которая образует с осью
,
которая образует с осью
![]() острый угол; 2) поток векторного поля
острый угол; 2) поток векторного поля
![]() через полную поверхность пирамиды
через полную поверхность пирамиды
![]() в направлении внешней нормали к ее
поверхности. Сделать чертеж.
в направлении внешней нормали к ее
поверхности. Сделать чертеж.
![]()
Решение:

1)
Поток поля
![]() через
через
![]() в направлении
в направлении
![]() .
.
![]()


![]() .
.
2)
Поток
![]() через пирамиду
через пирамиду
![]() .
.
![]()
Так как поверхность пирамиды замкнута, то по форму Гаусса-Остроградского:



![]()
Ответ:
1)
![]() ;
2)
;
2)
![]() .
.
301.
Проверить, будет ли поле вектора
![]() :
а) потенциальным; б) соленоидальным
? В случае потенциальности поля найти
его потенциал
:
а) потенциальным; б) соленоидальным
? В случае потенциальности поля найти
его потенциал
![]() :
:
![]()
Решение:
a)
Поле
![]() определено во всем пространстве, т.е. в
односвязной области,
определено во всем пространстве, т.е. в
односвязной области,
поэтому
для потенциальности достаточно
![]() .
Найдем:
.
Найдем:

![]() .
.
И
так поле
![]() потенциально. Для вычисления потенциала
по формуле
потенциально. Для вычисления потенциала
по формуле
![]() в качестве точки
в качестве точки
![]() возьмем начало координат. Тогда получаем:
возьмем начало координат. Тогда получаем:

б) Проверим соленоидальное поле вычислив:

Значит
поле
![]() не является соленоидным.
не является соленоидным.
Ответ:
Поле вектора
![]() потенциально
потенциально
![]() и не является соленоидальным
и не является соленоидальным
![]() .
.
