Высшая математика часть4 (3й вариант)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет непрерывного и дистанционного обучения

Специальность: Автоматизированные системы обработки информации

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №1

ВАРИАНТ №3

Группа

Зачетная книжка

Электронный адрес

483) Представить заданную функцию w=f (z), где z = x + iy, в виде w = u(x,y) + iv(x,y); проверить, является ли она аналитической. Если да, то найти значение ее производной в заданной точке z₀.

Решение.

Т.к. , то

Таким образом, действительная и мнимая части функции соответственно равны:

;

.

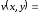
Эти функции, очевидно, являются дифференцируемыми функциями переменных х и у.

Проверим выполнение условий Коши-Римана. Для этого найдем частные производные этих функций.

;

;

;

.

Из полученных выражений видно, что для любых х и у

,

т.е. условия Коши-Римана выполняются для любых х и у. Следовательно, функция является аналитической во всей комплексной плоскости.

Вычислим производную этой функции

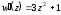
Вычислим значение производной этой функции при

.

493) Найти все лорановские разложения данной функции по степеням z - z₀ .

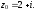
Решение.

Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z₁ = -1 и z₂ = 1, а точка особой не является. Вычислим и .

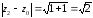Тогда кольца аналитичности функции: | z – 2 – i | < 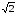, и

.

Запишем функцию в виде

и разложим ее на элементарные дроби:

При | z – 2 – i | < имеем: , ; .

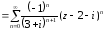Формула суммы бесконечно убывающей геометрической прогрессии справедлива, т.к. при | z – 2 – i | < ,

Таким образом, в круге | z – 2 – i | < функция раскладывается в ряд Тейлора:

В кольце

.

Формула суммы бесконечно убывающей геометрической прогрессии справедлива, т.к. при , .

,

Таким образом, в кольце функция раскладывается в ряд Лорана:

В кольце :

.

Формула суммы бесконечно убывающей геометрической прогрессии справедлива, т.к. при , .

,

.

В итоге в кольце имеем следующее разложение в ряд Лорана:

.

503) Определить область (круг) сходимости данного ряда и исследовать сходимость его (расходится, сходится условно, сходится абсолютно) в точках z₁, z₂ , z₃ .

Решение.

Найдем радиус сходимости данного степенного ряда по теореме Коши-Адамара:

.

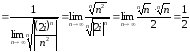Тогда область сходимости данного ряда , т.е. круг с центром в точке z₀ = -1 радиуса .

Т.к. точка лежит вне круга сходимости, то в этой точке данный ряд расходится.

Т.к. точка лежит на границе круга сходимости, то мы не можем использовать теорему Коши-Адамара. В этой точке получим числовой ряд

.

Исследуем полученный ряд на абсолютную сходимость, т.е. исследуем сходимость ряда

.

Хорошо известно, что числовые ряды вида сходятся при а > 1. Т.е. ряд сходится и, следовательно, исходный степенной ряд в точке сходится абсолютно.

Т.к. точка лежит внутри круга сходимости, то в этой точке исходный степенной ряд сходится абсолютно.

513) При помощи вычетов вычислить данный интеграл по контуру l.

Решение.

Подынтегральная функция имеет две особые точки – простой полюс и z = -2 – полюс второго порядка.

Внутри круга находятся обе эти точки.

Вычислим вычеты функции в этих точках.

Т.к. – простой полюс, то

.

Т.к. z = -2 – полюс второго порядка, то

.

Тогда по теореме Коши исходный интеграл будет равен:

.