
- •Решение задачи теплопроводности в бесконечном стержне методом Фурье.
- •Можно проверить, что функция
- •Частные решения уравнения Лапласа.
- •Общие свойства гармонических функций.
- •Основные свойства гармонических функций:
- •Краевые задачи для уравнения Лапласа.
- •Решение уравнения Лапласа методом разделения переменных.
Решение задачи теплопроводности в бесконечном стержне методом Фурье.
Рассмотрим тонкий длинный теплопроводящий стержень, боковая поверхность которого теплоизолирована. Уравнение теплопроводности для него имеет вид
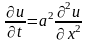
В
случае если стержень очень длинный, то
на процессы в средней его части условия
на границе не будут сказываться в
течение конечного времени. В таких
задачах стержень считается бесконечным.
В результате мы будем иметь только
начальное условие что соответствует
задаче Коши.

Сделаем замену переменных
 тогда
тогда
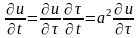
уравнение принимает вид
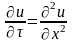
начальное
условие
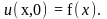 (1)
(1)
Ищем
решение в виде
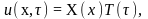
подставляя
его в (1) получаем
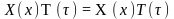 или
или
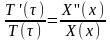
Так
как левая часть этого уравнение зависит
только от
 ,
а правая – только от x, то мы можем
сделать вывод, что равенство возможно
только в том случае, если и левая и
правая части равны одной и той же
константе:
,
а правая – только от x, то мы можем
сделать вывод, что равенство возможно
только в том случае, если и левая и
правая части равны одной и той же
константе:
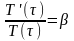
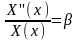
В
результате для Т(
)
получаем
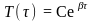
Так
как температура стержня должна оставаться
конечной при
 ,
то должно быть
,
то должно быть
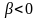 ,
т.е. мы можем положить
,
т.е. мы можем положить
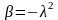 и
и

Уравнение для X(x) принимает вид
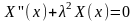 и его общее решение
и его общее решение
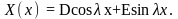
Тогда
частное решение уравнения (1) запишется
в виде
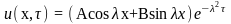 (2)
(2)
В
общем случае в (2) A = A(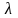 ),
B = B(
)
и семейство частных решений уравнения
(1) имеет вид
),
B = B(
)
и семейство частных решений уравнения
(1) имеет вид
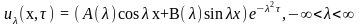
Общее решение уравнения (1) записывается как суперпозиция частных
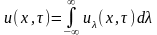 или
или
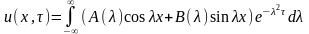 (3)
(3)
Неизвестные функции A( ) и B( ) подбираются так, чтобы удовлетворить начальному условию:
которое примет вид
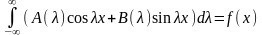 (4)
(4)
Равенство (3) представляет собой разложение функции f(x) в интеграл Фурье. Для нахождения неизвестных функций получаем следующие выражения:
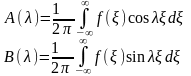
(5)
Подставляя (5) в (3) получаем
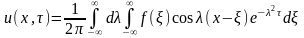
Т.о. мы получили решение задачи о теплопроводности в бесконечном стержне. Оно может быть преобразовано к виду
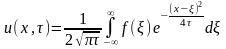 (6)
(6)
Далее
необходимо вернуться к исходной
переменной
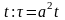 и, подставляя в (6), получим
и, подставляя в (6), получим
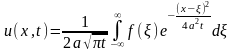 (7)
(7)
Можно проверить, что функция
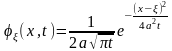
Также является решением исходного уравнения и называется фундаментальным решением уравнения теплопроводности.
Физическим тепловым импульсом называется начальное распределение температуры
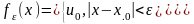
В этом случае решение задачи будет иметь вид
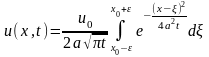
и по теореме о среднем оно может быть записано следующим образом

Точечный
тепловой импульс соответствует
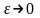 . Количество теплоты, переданное стержню,
пропорционально произведению
. Количество теплоты, переданное стержню,
пропорционально произведению
 И при
должно оставаться конечным
И при
должно оставаться конечным
=1
получаем, что
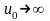 при
.
Т.о., точечный тепловой импульс может
быть записан в виде δ-функции Дирака:
при
.
Т.о., точечный тепловой импульс может
быть записан в виде δ-функции Дирака:
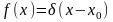
Подставляя записанное в таком виде начальное условие в (7), получаем решение
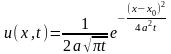
которое
есть фундаментальное решение
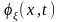 при
при
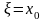
Решение задачи о теплопроводности для конечного отрезка.
Рассмотрим задачу о теплопроводности на отрезке:
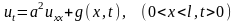
Начальное условие u(x,0) = f(x) и однородные граничные условия
u(0,t) = 0, u(l,t) = 0
Рассмотрим сначала однородную задачу
 Будем искать в
виде u(x,t) = X(x)T(t)
Будем искать в
виде u(x,t) = X(x)T(t)
Подставляя в уравнение, получаем
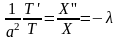
Получаем
два обыкновенных ДУ:
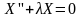
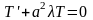
Из граничных условий для u получаем граничные условия для X: X(0) = 0, X(l) = 0.
В результате для функции X(x) получили задачу о собственных значениях (задачу Штурма-Лиувилля): X’’ +λX = 0, X(0) = 0, X(l) = 0. Собственные значения этой задачи:

соответствующие собственным функциям
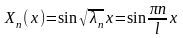
Находим
функцию T(t):

Частные
решения однородной задачи:
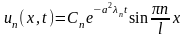
Общее решение задачи можно записать как суперпозицию частных

Из начального условия получаем
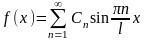 (1)
(1)
Последнее
выражение есть разложение функции f(x)
в ряд Фурье по синусам на интервале
(0,l).
Для нахождения
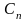 домножим уравнение (1) на
домножим уравнение (1) на
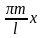 и
проинтегрируем:
и
проинтегрируем:
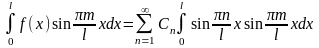
С
учетом формулы
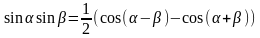
получим для интеграла в правой части

В
результате для коэффициента
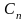 :
:
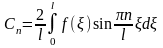
Подставим в решение найденное значение :
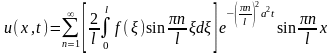 Поменяем порядок
суммирования и интегрирования
Поменяем порядок
суммирования и интегрирования
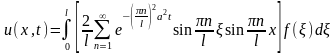
Введем функцию

G
- функция мгновенного точечного источника
или функции температурного влияния
мгновенного точечного источника тепла.
С ее использованием решение задачи
будет иметь вид
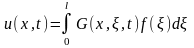
Функция G(x,ξ,t) представляет собой распределение температуры в стержне в момент времени t, если в начальный момент температура равна нулю и в этот момент в точке x = ξ мгновенно выделяется некоторое количество тепла, при том что на краях стержня поддерживается нулевая температура. Для количества тепла, выделившегося в некоторой окрестности точки ξ можно записать
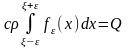
где
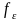 – температура в этой окрестности,
вызванная появлением тепла. Причем
равна
нулю всюду, кроме отрезка
– температура в этой окрестности,
вызванная появлением тепла. Причем
равна
нулю всюду, кроме отрезка
 Т.е.
Т.е.
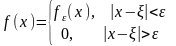
Решение записывается в виде

Воспользуемся теоремой о среднем
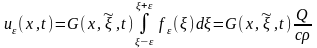
где
ξ – некоторая средняя точка интервала
 Полагая
Полагая
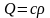 и ε→0, находим
и ε→0, находим

Таким
образом, мы доказали, что
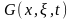 есть температура в точке x в момент t,
вызванная действием мгновенного
точечного источника величиной Q = cρ,
находящегося при t = 0 в точке x = ξ.Перейдем
к неоднородному уравнению теплопроводности
есть температура в точке x в момент t,
вызванная действием мгновенного
точечного источника величиной Q = cρ,
находящегося при t = 0 в точке x = ξ.Перейдем
к неоднородному уравнению теплопроводности
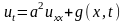
с нулевыми начальным и граничными условиями: u(x,0) = 0, u(0,t) = 0, u(l,t) = 0
Будем
искать решение в виде ряда по собственным
функциям задачи Штурма-Лиувилля

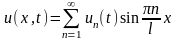
Разлагая g(x,t) в рад по тем же собственным функциям, будем иметь:
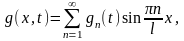 где
где

Подставляя все в исходное уравнение, получим
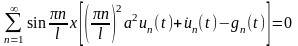
Отсюда получаем
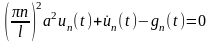 или
или
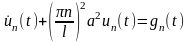
Из
начальных условий
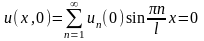
Отсюда
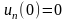 Получилось
неоднородное уравнение вида
Получилось
неоднородное уравнение вида
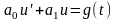
С
нулевым начальным условием u(0)=0
Его решение может быть записано в виде
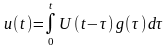
Что можно проверить простой подстановкой, здесь U(t)–решение однородного уравнения.
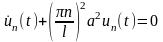
Подставляя
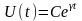 и подставляя в последнее уравнение,
получим
и подставляя в последнее уравнение,
получим
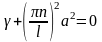 Отсюда
Отсюда
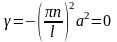
И
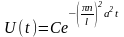
В
результате, для
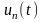 получаем
получаем

А решение неоднородного уравнения теплопроводности запишется в виде

Подставляя
сюда выражение для
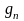 ,
получим
,
получим
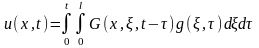 (2)
(2)
где функция источника определяется

Предположим,
что функция
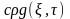 ,
представляющая собой плотность тепловых
источников,отлична от нуля только в
достаточно малой окрестности точки
,
представляющая собой плотность тепловых
источников,отлична от нуля только в
достаточно малой окрестности точки
 Тогда
общее количество тепла, выделяющееся
на отрезке (0,l) за время действия
источников, будет равно
Тогда
общее количество тепла, выделяющееся
на отрезке (0,l) за время действия
источников, будет равно
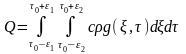
По теореме о среднем найдем
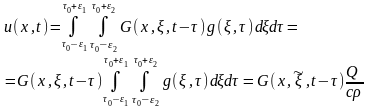 Переходя в последнем
уравнении к пределу
Переходя в последнем
уравнении к пределу
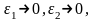 при этом
при этом
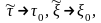 находим
находим

Если
положить Q =
 то
то
 есть фун-кция влияния мгновенного
источника тепла, со-средоточенного в
момент времени
есть фун-кция влияния мгновенного
источника тепла, со-средоточенного в
момент времени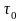 в
точке
в
точке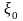
Если
тепловые источники действуют в области
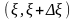 в течение времени
в течение времени
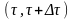 ,то
получаем
,то
получаем
 и
и
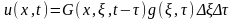
Если источники распределены непрерывно, то суммируя по всем источникам в области [0,l] за время [0,t], находим
Что совпадает с выражением (2). Т.о., решение (2) могло быть получено исходя из физического смысла функции источника.
Ортогональные криволинейные системы координат.
x,y,z
– декартовы координаты,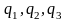 –
криволинейные координаты. Квадрат
элемента длины:
–
криволинейные координаты. Квадрат
элемента длины:
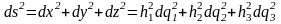
где
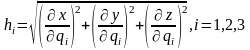
–метрические коэффициенты или коэффициенты Ламэ. Любая система криволинейных координат характеризуется набором координат. В криволинейных координатах:
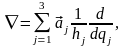
Оператор Лапласа:
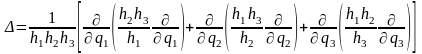
Цилиндрическая система координат
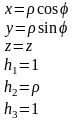
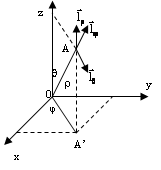
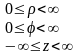
Поверхность
постоянной координаты
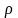 - это цилиндры, ось которых совпадает
с осью z.
Соответствующий единичный вектор
должен быть ортогонален этой поверхности.
- это цилиндры, ось которых совпадает
с осью z.
Соответствующий единичный вектор
должен быть ортогонален этой поверхности.
Поверхность
постоянной координаты
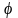 - это полуплоскости, ограниченные осью
z.
Соответствующий единичный вектор
перпендикулярен полуплоскости.
- это полуплоскости, ограниченные осью
z.
Соответствующий единичный вектор
перпендикулярен полуплоскости.
Поверхность
постоянной координаты z
- это плоскость, параллельная плоскости
xy.Соответствующий
единичный вектор перпендикулярен как
 так и
так и
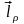 .
.
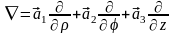
 Цилиндрическая
система координат
Цилиндрическая
система координат
Вместо
декартовых координат x,
y,
z
вводятся сферические координаты
 .
.
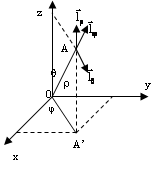
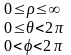
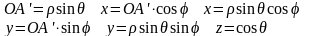
Поверхность постоянной координаты - сфера с центром в начале координат и радиусом .
Поверхность
постоянной координаты
 - это конусы, вершина конуса в точке О.
Раствор конуса направлен вверх. Угол
раствора конуса равен
- это конусы, вершина конуса в точке О.
Раствор конуса направлен вверх. Угол
раствора конуса равен
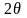
Поверхность постоянной координаты - это полуплоскость, ограниченная областью z.
Единичные вектора сферической системы координат:
- ортогонален сфере
 -
ортогонален конусу
-
ортогонален конусу
- ортогонален соответствующей плоскости.
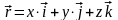
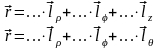
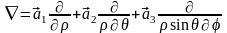

Распределение тепла в бесконечном цилиндре.
Рассмотрим цилиндр радиуса R, боковая поверхность которого поддерживается при постоянной температуре. Если в начальный момент времени температура в каждой точке зависит только от ее расстояния r до оси цилиндра, то и в последующие моменты времени температура будет зависеть только от r и t: u = u(r,t). Переходя в пространственном уравнении теплопроводности к цилиндрическим координатам, получим
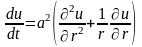 (1)
(1)- оператор Лапласа в
цилиндрической системе координат.
(1)
(1)- оператор Лапласа в
цилиндрической системе координат.
Начальное
условие
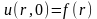
краевое
условие – условие постоянства температуры
боковой поверхности цилиндра –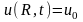
Рассмотрим
случай однородного краевого условия,
т.е.
 .В
противоположном случае надо сделать
замену
.В
противоположном случае надо сделать
замену
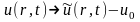
при этом само уравнение не изменится, а начальное и краевое условие примут вид
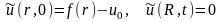
Будем решать задачу методом разделения переменных u(r,t) =U(r)T(t), в результате получим
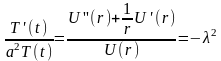
Находим

а для функции U(r) получаем уравнение
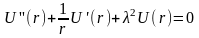
решением
которого является функция Бесселя
нулевого порядка
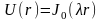
Из
краевого условия находим
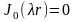
Т.е.,
собственные числа задачи выражаются
через нули функции Бесселя

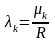
Каждому
собственному значению
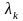 соответствует собственная функция
соответствует собственная функция
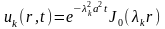 в результате
решение исходной задачи принимает вид
в результате
решение исходной задачи принимает вид
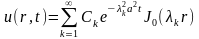
С учетом начального условия получаем
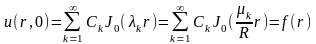
Сделаем
замену переменной
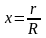 ,
в результате получим
,
в результате получим
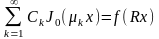
Находим
аналогичным образом коэффициенты
:
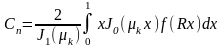
Уравнения эллиптического типа.
К уравнениям эллиптического типа обычно приводит рассмотрение стационарных процессов различной физической природы: колебания, теплопроводность, диффузия и т.д. Чаще всего встречается уравнение Лапласа:
Δu = 0
Функции, непрерывные в некоторой области вместе со своими производными до второго порядка включительно, и удовлетворяющие в этой области уравнению Лапласа, называются гармоническими.
Оператор Лапласа в декартовых координатах имеет вид:
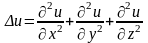
в циклических координатах.
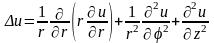
В сферических координатах
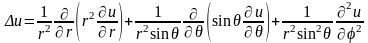
Задачи, приводящие к уравнению Лапласа.
Стационарное тепловое поле
В нестационарном случае температура удовлетворяет уравнению теплопроводности
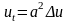
В стационарном случае, когда распределение температуры не меняется с течением времени u = u(x,y,z), приходим к уравнению Лапласа
Δu=0
В случае наличия тепловых источников получаем уравнение Пуассона Δu=-g
2. Электрическое поле неподвижных зарядов
Напряженность электрического поля удовлетворяет уравнению, выражающему теорему Гаусса в дифференциальной форме:
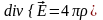 где
где
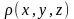 –
объемная плотность зарядов. Напряженность
поля связана со скалярным потенциалом
–
объемная плотность зарядов. Напряженность
поля связана со скалярным потенциалом
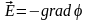
В результате получаем
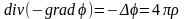 или
или

т.е. получили уравнение Пуассона. В случае отсутствия объемных зарядов приходим к уравнению Лапласа Δφ= 0.
