Размещено на http://www.allbest.ru/
Содержание
Простейшие движения твёрдого тела
2. Расчёт на прочность при растяжении и сжатии
3. Ременные и цепные передачи
4. Используемая литература
1. Простейшие движения твёрдого тела
Под абсолютно твердым телом в механике понимается такое тело, взаимное расстояние частей которого остается неизменным. Однако, любое тело конечные размеров считать состоящим из совокупности достаточно малых частиц – элементов, каждый из которых можно считать материальной точкой. Если тело абсолютно твердое, то для полного описания всевозможных его движений достаточно знать характер движения лишь нескольких точек данного тела.
Простейшим движением твердого тела является поступательное движение, при котором тело перемещается параллельно самому себе (рис. 2.1).
Поступательным движением твердого тела называют такое его движение, при котором каждая линия, соединяющая две любые точки тела, сохраняет неизменное направление в пространстве. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.
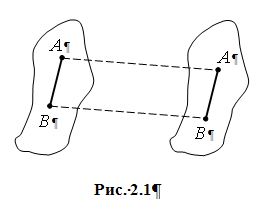
Исходя из определения поступательного движения все точки твердого тела обладают одинаковыми скоростями в любой момент времени, приращения векторов перемещений для всех точек одинаковы для одного и того же промежутка времени. Это обстоятельство позволяет свести изучение поступательного движения к задаче кинематики точки.
Вращательным движением называется такое движение, при котором траектории всех точек тела являются концентрическими окружностями, центры которых лежат на одной неподвижной прямой, называемой осью вращения.
Любое сложное движение твердого тела состоит из простых движений: поступательного и вращательного.
Вращение вокруг неподвижной оси
Пусть
твердое тело, вращаясь вокруг неподвижной
в данной системе отсчета оси
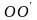совершило
за время
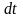бесконечно малый поворот (рис. 2.2).
Соответствующий угол поворота будем
характеризовать вектором
,
модуль которого равен углу поворота, а
направление совпадает с осью
,
причем так, что направление поворота
отвечает правилу правого винта (буравчика)
по отношению к направлению вектора
.
Теперь
найдем элементарное перемещение любой
точки
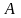твердого тела при таком повороте.
Положение точки
зададим радиус-вектором
,
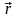проведенным из некоторой точки
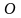на оси вращения. Тогда линейное перемещение
конца радиус-вектора
(рис. 2.2) связано с углом поворота
соотношением
или в векторном виде
.
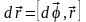(2.1)
Отметим, что это равенство справедливо лишь для бесконечно малого поворота .
Кроме того, введенный нами вектор удовлетворяет основному свойству векторов – векторному сложению (это можно доказать).
Заметим,
что при рассмотрении таких величин как
радиус-вектор
,
скорость
,
ускорение
,
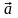не возникал вопрос о выборе их направления:
оно вытекало естественным образом из
природы самих величин. Подобные векторы
называют полярными.
В отличие от них векторы типа
,
направление которых связывают с
направлением вращения, называют
аксиальными,
или псевдовекторами.
Введем векторы угловой скорости и углового ускорения.
Вектор
угловой скорости
определяют как
,
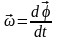(2.2)
где – промежуток времени, за который тело совершает поворот . Вектор совпадает по направлению с вектором и представляет собой аксиальный вектор.
Изменение
вектора
со временем характеризуют вектором
углового ускорения
,
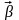который определяют как
.
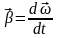(2.3)
Направление
вектора
совпадает с направлением
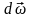– приращения вектора
.
Вектор
,
как и
,
является аксиальным.
Единицей угловой скорости в «СИ» является радиан в секунду (с-1), а единицей углового ускорения – радиан на секунду в квадрате (с-2).
В
проекциях на ось вращения
,
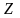положительное направление которого
свяжем с положительным направлением
отсчета координаты
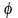– угла поворота – правилом правого
винта (рис. 2.3).
Тогда
проекци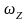и
и
векторов
и
определятся формулами
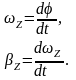(2.4)
Здесь
и
– величины алгебраические. Их знак
характеризует направление соответствующего
вектора. Например, если
,
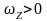то направление вектора
совпадает с положительным направлением
оси
;
если же
,
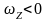то направление вектора
противоположно. Аналогично и для углового
ускорения.
Решение всех задач на вращение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки.
Достаточно
заменить линейные величины
,
,
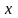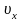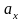на соответствующие угловые
,
,
и мы получим все закономерности и
соотношения для вращательного движения
тела.
Например, простейшие случаи вращения материальной точки вокруг неподвижной оси:
а) равномерное вращение
;
;
;
;
;
,
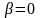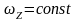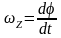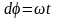при
;
;
.
;
.
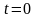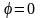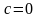Если
движение происходит по окружности, то
время, за которое происходит один оборот,
то есть
,
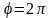называют периодом
;
.
б) равнопеременное вращение
;
;
;
,
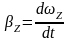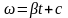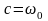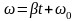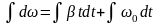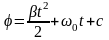при
;
;
;
;
;
;
;
при
;
;
.
.
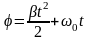Связь между линейными и угловыми величинами
Найдем скорость производной точки твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью . Пусть положение точки относительно некоторой точки оси вращение характеризуется радиус-вектором (рис. 2.4.).
Записав
(2. 5)
и поделив ее на соответствующий промежуток времени , получим
;
,
то
,
(2.6)
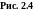
то есть скорость любой точки твердого тела, вращающегося вокруг некоторой оси с угловой скоростью , равна векторному произведению на радиус-вектор точки относительно произвольной точки оси вращения.
Модуль вектора
,
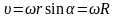где
– радиус окружности, по которой движется
точка
.
Продифференцировав (2.6) по времени, найдем полное ускорение точки :
.
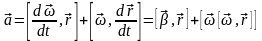(2.7)
В
данном случае (ось вращения неподвижна)
,
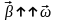поэтому вектор
представляет собой тангенциальное
ускорение
.
Вектор же
– нормальное
.
Модули этих ускорений
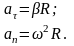
Отсюда модуль полного ускорения
.
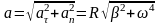(2.8)