
- •Принцип независимости действия сил
- •Абсолютно упругий и неупругий удар
- •1)Идеальный газ
- •Классический идеальный газ
- •Квантовый идеальный газ
- •Ферми-газ
- •Бозе-газ
- •Электростатическая индукция в проводниках
- •Электростатическая индукция в диэлектриках
- •Плотность зарядов (линейная поверхностная, объемная)
- •Другие определения
- •[Править]Теплоёмкость для различных состояний вещества
- •[Править]Теория теплоёмкости
- •Майера уравнение
- •Теория теплоёмкости Эйнштейна
- •[Править]Недостатки теории
- •Модель Дебая
- •История
- •Физический смысл адиабатического процесса Работа газа
- •[Править]Внутренняя энергия идеального газа
- •[Править]Адиабатический процесс
- •[Править]Энтропия и обратимость
- •Уравнение Пуассона для идеального газа [править]Адиабата Пуассона
- •[Править]Вывод уравнения
- •Описание цикла Карно
- •[Править]кпд тепловой машины Карно
- •[Править]Связь между обратимостью цикла и кпд
- •Формулировки
- •[Править]Ограничения
- •[Править]Второе начало термодинамики и «тепловая смерть Вселенной»
- •[Править]Энтропия и критика эволюционизма
- •Общее описание
- •[Править]Уравнения Фика
- •[Править]Геометрическое описание уравнения Фика
- •Закон теплопроводности Фурье
- •[Править]Коэффициент теплопроводности вакуума
- •[Править]Связь с электропроводностью
- •[Править]Коэффициент теплопроводности газов
- •[Править]Обобщения закона Фурье
- •Сила вязкого трения
- •[Править]Вторая вязкость
- •[Править]Вязкость газов
- •[Править]Влияние температуры на вязкость газов
- •Вязкость жидкостей [править]Динамический коэффициент вязкости
- •[Править]Кинематическая вязкость
- •[Править]Ньютоновские и неньютоновские жидкости
- •[Править]Вязкость аморфных материалов
- •[Править]Физика реального газа
- •Уравнение состояния
- •Внутренняя энергия газа Ван-дер-Ваальса
- •Критические параметры
- •Приведённые параметры
- •Недостатки уравнения Ван-дер-Ваальса
- •Коэффициент k
- •[Править]Закон Кулона в квантовой механике
- •[Править]Закон Кулона с точки зрения квантовой электродинамики
- •[Править]История
- •[Править]Закон Кулона, принцип суперпозиции и уравнения Максвелла
- •[Править]Cтепень точности закона Кулона
- •[Править]Поправки к закону Кулона в квантовой электродинамике
- •[Править]Закон Кулона и поляризация вакуума
- •[Править]Закон Кулона и сверхтяжелые ядра
- •[Править]Значение закона Кулона в истории науки
- •Лектрический заряд, напряжение, потенциал
- •[Править]Принцип суперпозиции в электродинамике
- •[Править]Примеры нарушения электродинамического принципа суперпозиции
- •[Править]Отсутствие принципа суперпозиции в нелинейных теориях
- •Поток вектора напряженности электрического поля. Теорема Гаусса
- •Теорема Остроградского—Гаусса и ее применение для расчета электростатических полей
- •Равномерно заряженная бесконечная плоскость
- •Бесконечная равномерно заряженная нить
- •Разность потенциалов
- •32 Диэлектрики в электрическом поле. Вектор поляризации. Диэлектрическая восприимчивость вещества. Диэлектрическая проницаемость. Электрическое смещение.
- •Типы поляризации
- •[Править]Зависимость вектора поляризации от внешнего поля [править]в постоянном поле [править]в слабых полях
- •[Править]в сильных полях
- •[Править]в зависящем от времени поле
- •Зависимость от времени
- •[Править]Тензор поляризуемости
- •Практическое применение
- •[Править]Зависимость от частоты
- •Электроемкость. Конденсаторы
- •Проводники электричества
- •Электрические изоляторы
- •Гальванические элементы
- •Закон Ома для неоднородного участка цепи
2. Скорость. Средняя скорость. Мгновенная скорость. Ускорение и его составляющие.
Средняя скорость
![]()
В
некоторых случаях, когда имеют дело с
неравномерным движением, пользуются
так называемой средней
скоростью.
Если
тело совершило некоторое перемещение ![]() за
промежуток времени t, то, разделив
на
t, мы получим среднюю
скорость:
за
промежуток времени t, то, разделив
на
t, мы получим среднюю
скорость:
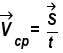
Таким образом, средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени. Если, например, поезд проходит 600 км за 10 ч, то это значит, что в среднем он каждый час проходит 60 км:
![]()
Но
ясно, что какую-то часть времени поезд
вовсе не двигался, а стоял на остановке;
трогаясь со станции, поезд увеличивал
свою скорость, приближаясь к ней —
уменьшал ее. Все это при определении
средней скорости мы не принимаем во
внимание и считаем, что поезд каждый
час проходит по 60 км, каждые полчаса —
по 30 км и т. д. Пользуясь формулой
,
мы как бы считаем, что поезд.совершает
равномерное движение с постоянной
скоростью,
равной Vcp, хотя, быть может,
за все время движения не было ни одного
такого часа, за который он прошел бы
именно 60 км. Но знание средней скорости
позволяет определить перемещение по
формуле: ![]() .
Но
при этом надо помнить, что эта формула
дает верный результат только для того
участка траектории, для которого
определена средняя скорость. Если,
пользуясь значением средней скорости
в 60 км/ч, вычислять перемещение не за 10
ч, а за 2, 4 или 5 ч, то мы получим неверный
результат. Это объясняется тем, что
средняя скорость за время 10 ч не равна
средним скоростям за 2, 4 и 5 ч.
Таким
образом, при помощи понятия средней
скорости основную задачу механики —
определить положение тела в любой момент
времени — решить нельзя.
Все же во
многих случаях знание средней скорости
может оказаться полезным. Если, например,
туристам из их прежнего опыта или из
опыта их товарищей известно, что по
горной дороге можно продвигаться со
средней скоростью 2 км/ч, то они, собираясь
в новый поход в горный район, могут
воспользоваться этим, чтобы заранее
определить место, куда они придут к
исходу дня.
Часто, говоря о средней
скорости, подразумевают не вектор
,
а скалярную величину, определяемую
длиной пути, которую тело в среднем
проходит за единицу времени:
.
Но
при этом надо помнить, что эта формула
дает верный результат только для того
участка траектории, для которого
определена средняя скорость. Если,
пользуясь значением средней скорости
в 60 км/ч, вычислять перемещение не за 10
ч, а за 2, 4 или 5 ч, то мы получим неверный
результат. Это объясняется тем, что
средняя скорость за время 10 ч не равна
средним скоростям за 2, 4 и 5 ч.
Таким
образом, при помощи понятия средней
скорости основную задачу механики —
определить положение тела в любой момент
времени — решить нельзя.
Все же во
многих случаях знание средней скорости
может оказаться полезным. Если, например,
туристам из их прежнего опыта или из
опыта их товарищей известно, что по
горной дороге можно продвигаться со
средней скоростью 2 км/ч, то они, собираясь
в новый поход в горный район, могут
воспользоваться этим, чтобы заранее
определить место, куда они придут к
исходу дня.
Часто, говоря о средней
скорости, подразумевают не вектор
,
а скалярную величину, определяемую
длиной пути, которую тело в среднем
проходит за единицу времени:
![]()
Если
тело не меняет направления своего
движения, то эта средняя скорость
совпадает с абсолютным значением
вектора
так
как в этом случае l = |s|. В случае, когда
тело движется по сложной не прямолинейной
траектории (например, автомобиль в
городе), эти величины не совпадают. О
какой величине идет речь, обычно бывает
ясно из условия задачи. Когда, например,
диспетчер в гараже определяет, какой
запас горючего необходим автомобилю
на день, он пользуется формулой
.
Зная среднюю скорость автомобиля в
городе, т. е. расстояние, которое он в
среднем проходит за 1 ч, можно определить
длину пути, которую он пройдет за
определенное время, и, следовательно,
необходимый запас горючего. В данной
задаче нельзя воспользоваться определением
средней скорости как вектора:
ведь перемещение s
автомобиля за день равно нулю — он
выехал из гаража и затем в него вернулся.
Поэтому ![]()
Мгновенная скорость
Мы сделали попытку свести неравномерное движение к равномерному и для этого ввели среднюю скорость движения. Но это нам не помогло: зная среднюю скорость, нельзя решать самую главную задачу механики — определять положение тела в любой момент времени. Можно ли каким-нибудь другим способом свести неравномерное движение к равномерному? Этого, оказывается, сделать нельзя, потому что механическое движение — это процесс непрерывный. Непрерывность движения состоит в том, что если, например, тело (или точка), двигаясь прямолинейно с возрастающей скоростью, перешло из точки А в точку В, то оно непременно должно побывать во всех промежуточных точках, лежащих между А и В, без всяких пропусков. Но это еще не все. Предположим, что, подходя к точке А, тело двигалось равномерно со скоростью 5 м/сек, а после прохождения точки В оно двигалось тоже равномерно, но со скоростью 30 м/сек. При этом на прохождение участка АВ тело потратило 15 сек. Следовательно, на отрезке АВ скорость тела за 15 сек изменилась на 25 м/сек. Но так же как тело при своем движении не могло миновать ни одну из точек на его пути, его скорость должна была принять все значения скорости между 5 и 30 м/сек. Тоже без всяких пропусков! В этом и состоит непрерывность механического движения: ни координаты тела, ни его скорость не могут изменяться скачками. Отсюда можно сделать очень важный вывод. Различных значений скорости в интервале от 5 до 30 м/сек имеется бесчисленное множество (в математике говорят, бесконечно много значений). Но между точками А и В имеется и бесчисленное множество (бесконечно много!) точек, а 15-секундный интервал времени, в течение которого тело переместилось из точки А в точку В, состоит из бесчисленного множества промежутков времени (время тоже течет без скачков!). Следовательно, в каждой точке траектории движения и в каждый момент времени тело обладало определенной скоростью. Скорость, которую имеет тело в данный момент времени и в данной точке траектории, называют мгновенной скоростью. При равномерном прямолинейном движении скорость тела определяется отношением его перемещения к промежутку времени, за который совершено это перемещение. Что же означает скорость в данной точке или в данный момент времени? Допустим, что некоторое тело (как всегда, мы в действительности имеем в виду какую-то определенную точку этс=го тела) движется прямолинейно, но не равномерно. Как вычислить его мгновенную скорость в некоторой точке А его траектории? Выделим небольшом участок l на этой траектории, включающий точку А (Рис. 1)

Малое перемещение
тела на
этом участке обозначим через ![]() ,
а малый промежуток времени, в течение
которого оно совершено,.
через
,
а малый промежуток времени, в течение
которого оно совершено,.
через ![]() .
Разделив
на
,
мы получим среднюю скорость на этом
участке: ведь скорость изменяется
непрерывно и в разных местах участка l
она различна.
Уменьшим теперь длину
участка l. Выберем участок 2 (см. рис. 1),
тоже включающий в себя точку А. На этом
меньшем участке
перемещение равно
.
Разделив
на
,
мы получим среднюю скорость на этом
участке: ведь скорость изменяется
непрерывно и в разных местах участка l
она различна.
Уменьшим теперь длину
участка l. Выберем участок 2 (см. рис. 1),
тоже включающий в себя точку А. На этом
меньшем участке
перемещение равно  и
проходит его тело за промежуток времени
и
проходит его тело за промежуток времени ![]() .
Ясно, что на участке 2 скорость тела
успевает измениться на меньшую величину.
Но отношение
.
Ясно, что на участке 2 скорость тела
успевает измениться на меньшую величину.
Но отношение ![]() дает
нам и для этого меньшего участка все же
среднюю скорость. Еще меньше изменение
скорости на протяжении участка 3 (также
включающего в себя точку А), меньшего,
чем участки l и 2, хотя,
разделив
перемещение
дает
нам и для этого меньшего участка все же
среднюю скорость. Еще меньше изменение
скорости на протяжении участка 3 (также
включающего в себя точку А), меньшего,
чем участки l и 2, хотя,
разделив
перемещение ![]() на
промежуток времени
на
промежуток времени ![]() ,
мы опять получим среднюю скорость на
этом малом участке траектории. Будем
постепенно уменьшать длину участка, а
вместе с ним и промежуток времени, за
который тело проходит этот участок. В
конце концов мы стянем участок траектории,
прилегающей к точке А, в самую точку А,
а промежуток времени — в момент времени.
Тогда-то средняя скорость и станет мгновенной
скоростью,
потому что на достаточно малом участке
изменение скорости будет настолько
мало, что его можно не учитывать, значит,
можно считать, что скорость не
изменяется.
Мгновенная
скорость, или скорость в данной точке,
равна отношению достаточно малого
перемещения на малом участке траектории,
прилегающей к этой точке, к малому
промежутку времени, в течение которого
совершается это перемещение.
Понятно,
что скорость равномерного прямолинейного
движения — это одновременно его
мгновенная и средняя скорость.
Мгновенная
скорость — величина векторная. Ее
направленна совпадает с направлением
перемещения (движения) в данной
точка
Прием, к которому мы прибегли,
чтобы пояснить смысл мгновенной скорости,
состоит, таким образом, в следующем.
Участок траектории и время, в течение
которого он проходится, мы мысленно
постепенно уменьшаем до тех пор, пока
участок уже нельзя отличить от точки,
промежуток времени — от момента времени,
а неравномерное движение — от равномерного.
Таким приемом всегда пользуются, когда
изучают явления, в которых играют роль
какие-нибудь непрерывно изменяющиеся
величины.
Нам остается теперь
выяснить, что
необходимо знать для нахождения
мгновенной скорости тела в
любой точке траектории и в любой момент
времени.
,
мы опять получим среднюю скорость на
этом малом участке траектории. Будем
постепенно уменьшать длину участка, а
вместе с ним и промежуток времени, за
который тело проходит этот участок. В
конце концов мы стянем участок траектории,
прилегающей к точке А, в самую точку А,
а промежуток времени — в момент времени.
Тогда-то средняя скорость и станет мгновенной
скоростью,
потому что на достаточно малом участке
изменение скорости будет настолько
мало, что его можно не учитывать, значит,
можно считать, что скорость не
изменяется.
Мгновенная
скорость, или скорость в данной точке,
равна отношению достаточно малого
перемещения на малом участке траектории,
прилегающей к этой точке, к малому
промежутку времени, в течение которого
совершается это перемещение.
Понятно,
что скорость равномерного прямолинейного
движения — это одновременно его
мгновенная и средняя скорость.
Мгновенная
скорость — величина векторная. Ее
направленна совпадает с направлением
перемещения (движения) в данной
точка
Прием, к которому мы прибегли,
чтобы пояснить смысл мгновенной скорости,
состоит, таким образом, в следующем.
Участок траектории и время, в течение
которого он проходится, мы мысленно
постепенно уменьшаем до тех пор, пока
участок уже нельзя отличить от точки,
промежуток времени — от момента времени,
а неравномерное движение — от равномерного.
Таким приемом всегда пользуются, когда
изучают явления, в которых играют роль
какие-нибудь непрерывно изменяющиеся
величины.
Нам остается теперь
выяснить, что
необходимо знать для нахождения
мгновенной скорости тела в
любой точке траектории и в любой момент
времени.
Ускорение. Равноускоренное движение
Механика » Кинематика Автор: admin
При
неравномерном движении мгновенная
скорость тела непрерывно изменяется:
от точки к точке, от одного момента
времени к другому. Как же вычислить
скорость в любой момент времени?
Для
этого нужно знать, как быстро изменяется
скорость, или, другими словами, каково
ее изменение в единицу времени.
Для
простоты мы будем рассматривать такое
неравномерное движение тела, при котором
его скорость за любые равные промежутки
времени изменяется одинаково. Такое
движение называется равноускоренным.
Движение,
при котором скорость за любые равные
промежутки времени изменяется одинаково,
называют равноускоренным движением.
Если
в некоторый начальный момент времени
скорость тела равна ![]() ,
а через промежуток времени t она
оказывается равной
,
а через промежуток времени t она
оказывается равной ![]() ,
то за каждую единицу времени скорость
изменяется на
,
то за каждую единицу времени скорость
изменяется на![]() Величина
характеризует
быстроту изменения скорости. Ее называют
ускорением и обозначают буквой
Величина
характеризует
быстроту изменения скорости. Ее называют
ускорением и обозначают буквой ![]() :
:
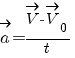 (1)
(1)
Ускорением
движущегося тела называют величину,
равную отношению изменения скорости
тела к промежутку времени, в течение
которого это изменение произошло.
Если
ускорение тела по абсолютному значению
велико, то это значит, что оно быстро
набирает скорость (когда тело разгоняется),
или быстро теряет ее (при торможении).
Если
ускорение
известно,
то можно вычислить значение скорости
тела
в любой момент времени, если известно
еще и значение начальной
скорости
.
Действительно,
из формулы (1) следует, что ![]() Ускорение
и нужно знать для вычисления скорости
.
Так
как ускорение равно произведению
векторной величины
Ускорение
и нужно знать для вычисления скорости
.
Так
как ускорение равно произведению
векторной величины ![]() на
скаляр
на
скаляр ![]() ,
оно само является векторной величиной.
В
каких единицах измеряют ускорение?
Так
как
,
то абсолютное значение ускорения равно
единице, если равно единице абсолютное
значение изменения скорости и равен
единице промежуток времени.
За
единицу ускорения принимают ускорение
такого движения, при котором за единицу
времени скорость изменяется на единицу
скорости.
В
системе единиц СИ скорость
измеряется в метрах в секунду,
а время — в секундах, так чтоускорение
измеряется в метрах в секунду за
секунду или
в метрах на секунду в квадрате
,
оно само является векторной величиной.
В
каких единицах измеряют ускорение?
Так
как
,
то абсолютное значение ускорения равно
единице, если равно единице абсолютное
значение изменения скорости и равен
единице промежуток времени.
За
единицу ускорения принимают ускорение
такого движения, при котором за единицу
времени скорость изменяется на единицу
скорости.
В
системе единиц СИ скорость
измеряется в метрах в секунду,
а время — в секундах, так чтоускорение
измеряется в метрах в секунду за
секунду или
в метрах на секунду в квадрате ![]() .
.
Направление ускорения
Механика » Кинематика Автор: admin
При
прямолинейном движении векторы
и
направлены
вдоль одной прямой, которая является в
то же время и траекторией движения.
Вдоль этой же прямой в направлении
движения тела мы условились направлять
и координатную ось (ось X). В таком случае
вектор разности
,
а значит и вектор ускорения
,
лежит на той же прямой. Но куда он
направлен — в сторону движения (так же
как ось X) или против него?
Проекция
разности двух векторов на какую-нибудь
ось равна разности их проекций на ту же
ось. Следовательно, для проекций
векторов ![]() и
на
ось X можно написать
и
на
ось X можно написать
![]() (1)
(1)
Здесь
а — проекция вектора
на
ось X; ![]() и
и ![]() -
проекции векторов
и
-
проекции векторов
и ![]() на
ту же ось.
Так как все три вектора
лежат па одной прямой (оси X), то абсолютные
значения их проекций равны абсолютным
значениям самих векторов.
Рассмотрим
2 случая ускоренного движения тела.
Первый
случай. Скорость
тела по абсолютному значению растет
(тело «разгоняется»). Это значит, что
на
ту же ось.
Так как все три вектора
лежат па одной прямой (оси X), то абсолютные
значения их проекций равны абсолютным
значениям самих векторов.
Рассмотрим
2 случая ускоренного движения тела.
Первый
случай. Скорость
тела по абсолютному значению растет
(тело «разгоняется»). Это значит, что ![]() .
Тогда из формулы (1) видно, что проекция
ускорения а положительна и равна
.
Тогда из формулы (1) видно, что проекция
ускорения а положительна и равна ![]() .
Вектор
,
следовательно, направлен так же, как
ось X, то есть в сторону движения.
Второй
случай. Тело
тормозится, то есть абсолютное значение
его скорости уменьшается
.
Вектор
,
следовательно, направлен так же, как
ось X, то есть в сторону движения.
Второй
случай. Тело
тормозится, то есть абсолютное значение
его скорости уменьшается ![]() .
Из
формулы (I) можно получить выражение для
скорости
:
.
Из
формулы (I) можно получить выражение для
скорости
:
![]() (2)
(2)
В
этой формуле, повторяем, а — проекция
вектора
на
ось X;
и
-
проекции векторов
и
на
ту же ось, которые могут быть как
положительными, так и отрицательными.
При
решении задач выражение для скорости
(2) удобно записывать так, чтобы из него
сразу было видно, как направлен вектор
ускорения.
Если скорость тела растет
(разгон), то ![]() и
и
![]() (2а)
(2а)
Когда
же скорость тела уменьшается
(торможение), ![]()
![]() (2б)
Понятно,
что тело, которое тормозится, должно
когда-то остановиться. Это произойдет,
как это видно из формулы (2б), тогда,
когда
станет
равным
(2б)
Понятно,
что тело, которое тормозится, должно
когда-то остановиться. Это произойдет,
как это видно из формулы (2б), тогда,
когда
станет
равным ![]() ,
т. е. в момент времени
,
т. е. в момент времени 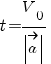 .
Но если ускорение остается постоянным
(по модулю и направлению) и после этого
момента, то тело, остановившись, начнет
двигаться в противоположную сторону.
Это видно из того, что при
.
Но если ускорение остается постоянным
(по модулю и направлению) и после этого
момента, то тело, остановившись, начнет
двигаться в противоположную сторону.
Это видно из того, что при  станет
больше, чем
,
скорость
изменит
свои знак на обратный. Так движется,
например, тело, брошенное вертикально
вверх: долетев до высшей точки траектории,
тело начинает движение вниз.
Если
станет
больше, чем
,
скорость
изменит
свои знак на обратный. Так движется,
например, тело, брошенное вертикально
вверх: долетев до высшей точки траектории,
тело начинает движение вниз.
Если ![]() и
вектор ускорения направлен так же, как
и ось координат, то из формулы (2а) следует,
что
и
вектор ускорения направлен так же, как
и ось координат, то из формулы (2а) следует,
что
![]()
Если же ось координат выбрана так, что направление вектора ускорения противоположно направлению оси координат, то из формулы (2б) следует, что
![]()
Знак «-» в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем. Обычно мы называем движение с возрастающей по абсолютной величине скоростью ускоренным движением, а движение с убывающей скоростью — замедленным движением. Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения. Мы знаем, что и перемещение, и скорость, и траектория движения различны относительно разных тел отсчета, движущихся друг относительно друга. А ускорение? Относительно ли оно? Ускорение тела, как мы теперь знаем, определяется векторной разностью двух значений его скорости в различные моменты времени. При переходе от одной системы координат к другой, движущейся относительно первой равномерно и прямолинейно, изменятся оба значения скорости. Но изменятся они на одну и ту же величину. Разность же их останется неизменной. Поэтому и ускорение останется неизменным. Во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, ускорение тела одинаково. Но ускорения тела будут различными в системах отсчета, движущихся с ускорением друг относительно друга. В этом случае ускорения складываются так же, как скорости.
3 Кинематика вращательного движения. Угловые скорость и ускорение. Связь между линейными и угловыми величинами.
Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.
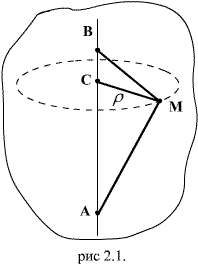
Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться.
При описании вращательного движения твердого тела относительно неподвижной в данной системе отсчета принято использовать векторные величины особого рода. В отличие от рассмотренных выше полярных векторов r (радиус-вектор), v (скорость), a (ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными (лат. axis – ось).
Элементарный поворот dφ – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта.
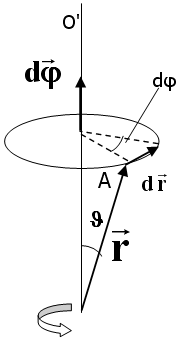 Рис.1.4.
К определению направления аксиального
вектора
Рис.1.4.
К определению направления аксиального
вектора
Линейное перемещение dr произвольной точки А твердого тела связано с радиусом-вектором r и поворотом dφ соотношением dr=rsinα•dφ или в векторном виде через векторное произведение:
dr=[dφ,r] (1.9)
Соотношение (1.9) справедливо именно для бесконечно малого поворота dφ.
Угловая скорость ω – аксиальный вектор, определяемый производной вектора поворота по времени:
ω=dφ/dt=φ'
Вектор ω, как и вектор dφ, направлен вдоль оси вращения по правилу правого винта (рис.1.5).
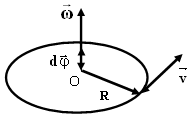 Рис.1.5.
К определению направления вектора
Рис.1.5.
К определению направления вектора
Угловое ускорение β – аксиальный вектор, определяемый производной вектора угловой скорости по времени:
β=dω/dt=d2φ/dt2=ω'=φ''
При ускоренном движении вектор β по направлению совпадает с ω (рис. 1.6,а), а при замедленном - векторы β и ω направлены противоположно друг другу (рис. 1.6,б).
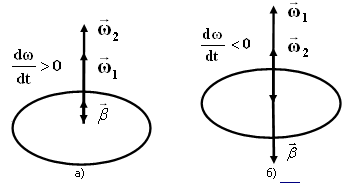 Рис.1.6.
Связь между направлениями векторов ω
и β
Рис.1.6.
Связь между направлениями векторов ω
и β
Важное замечание: решение всех задач на вращение твердого тела вокруг неподвижной оси по форме аналогично задачам на прямолинейное движение точки. Достаточно заменить линейные величины x, vx, ax на соответствующие им угловые φ, ω и β, и мы получим уравнения, аналогичные (1.6) -(1.8).
Угловая скорость.
Векторная величина
|
(2.1) |
называется
угловой скоростью тела. Вектор ![]() направлен
вдоль мгновенной оси вращения в сторону,
определяемую правилом винта, т.е. также
как вектор элементарного поворота
направлен
вдоль мгновенной оси вращения в сторону,
определяемую правилом винта, т.е. также
как вектор элементарного поворота ![]() . Модуль
вектора угловой скорости равен
. Модуль
вектора угловой скорости равен ![]() .
Вращение с постоянной угловой скоростью
называется равномерным, при этом:
.
Вращение с постоянной угловой скоростью
называется равномерным, при этом:
![]()
т.е.
при равномерном вращении ![]() показывает,
на какой угол поворачивается тело за
единицу времени.
показывает,
на какой угол поворачивается тело за
единицу времени.
Угловое ускорение.
В
случае неравномерного движения ![]() не
остается постоянной. Величина,
характеризующая скорость изменения
угловой скорости называется угловым
ускорением и равна:
не
остается постоянной. Величина,
характеризующая скорость изменения
угловой скорости называется угловым
ускорением и равна:
|
(2.5) |
В
случае вращения тела вокруг
неподвижной
оси изменение вектора
обусловлено
толькоизменением его численного
значения. При этом вектор ![]() углового
ускорения направлен вдоль оси вращения
в ту же сторону, что и
при
ускоренном вращении
углового
ускорения направлен вдоль оси вращения
в ту же сторону, что и
при
ускоренном вращении ![]() и
при замедленном
и
при замедленном ![]() в
обратном направлении. ( рис 2.3 а),б) )
в
обратном направлении. ( рис 2.3 а),б) )
Связь между линейными и угловыми величинами.
Отдельные
точки вращающегося тела имеют различные
линейные скорости ![]() .
Скорость каждой точки, будучи направлена
по касательной к соответствующей
окружности, непрерывно изменяет свое
направление. Величина
скорости
.
Скорость каждой точки, будучи направлена
по касательной к соответствующей
окружности, непрерывно изменяет свое
направление. Величина
скорости ![]() определяется
скоростью вращения тела
и
расстоянием R рассматриваемой точки от
оси вращения. Пусть за малый промежуток
времени
определяется
скоростью вращения тела
и
расстоянием R рассматриваемой точки от
оси вращения. Пусть за малый промежуток
времени ![]() тело
повернулось на угол
тело
повернулось на угол![]() (рис
2.4). Точка, находящаяся на расстоянии R
от оси проходит при этом путь, равный
(рис
2.4). Точка, находящаяся на расстоянии R
от оси проходит при этом путь, равный
![]()
Линейная скорость точки по определению.
|
(2.6) |
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:
![]()
подставляя значение скорости из (2.6), находим:
|
(2.7) |
Тангенциальное ускорение
![]()

Воспользовавшись тем же отношением (2.6) получаем
|
(2.8) |
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.
4 Динамика материальной точки и поступательного движения твердого тела. Законы Ньютона. Масса. Сила.
Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.Первый закон Ньютона показывает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания внешних воздействий: В этом проявляется особое динамическое свойство тел, называемое инертностью. Соответственно первый закон Ньютона обычно называют законом инерции, а движение тела, свободного от внешних воздействий - движением по инерции.
Опыт показывает, что первый закон Ньютона выполняется не во всякой системе отсчета. Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета. То есть, это такие системы отсчета, относительно которых материальная точка, на которую не действуют другие тела, либо покоится, либо движется равномерно и прямолинейно.
Сила
С точки зрения наших личных наблюдений, с чем мы связываем «причину движения»? Можно ответить, с мускульной тягой или с толчком. Чтобы передвинуть стол, мы должны его очень сильно толкать, тогда как для перемещения листа бумаги по письменному столу вам достаточно лишь незначительного усилия. Эти тяговые и толкающие усилия мы называем силами. Таким образом, под силой мы понимаем физическую величину, которая является мерой механического воздействия на тело со стороны других тел.
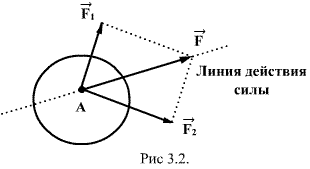
Сила,
приложенная к телу, полностью определена,
если указаны ее численное значение,
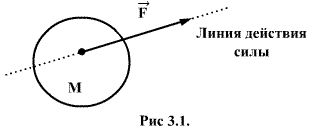
направление действия и точка; приложения
М (рис.3.1). Прямую, проведенную через
точку приложения силы в направлении
действия силы, называют линией действия
силы. Две силы называются численно
равными и противоположными по направлению,
если одновременное приложение этих сил
в одной и той же точке тела не вызывает
изменения его механического движения.
В частности, если до приложения таких
двух сил тело покоилось, то оно продолжает
оставаться в покое и после их приложения.
Поэтому говорят, что две численно равные
и противоположно направленные силы,
приложенные в одной и той же точке тела,
взаимно уравновешиваются. Если на тело
одновременно действует n сил, приложенных
в одной точке Атела,
то их можно заменить одной эквивалентной
силой ![]() ,
равно их геометрической сумме
,
равно их геометрической сумме
|
(3.1) |
и приложенной в той же точке. Эта сила называется результирующей или равнодействующей силой. Действие силы на абсолютно твердое тело не изменяется при переносе точки ее приложения вдоль линии действия.
2закон Н. масса
Опыт
показывает, что под действием
силы
свободное
тело изменяет скорость своего
поступательного движения, приобретая
ускорение ![]() . При
этом ускорение тела прямо пропорционально
вызывающей его силе и совпадает с ней
по направлению:
. При
этом ускорение тела прямо пропорционально
вызывающей его силе и совпадает с ней
по направлению:
![]()
где ![]() -
положительный коэффициент пропорциональности,
постоянный для каждого конкретного
тела.
-
положительный коэффициент пропорциональности,
постоянный для каждого конкретного
тела.
Величина ускорения, приобретенного под действием силы , зависит от тела, на которое действует сила. Так как большим телам труднее придать ускорение, чем малым, принято пропорциональность между силой и ускорением выражать в следующем виде:
|
(3.2) |
Коэффициент пропорциональности m зависит от предмета. Его величина растет с увеличением размеров тел, если они однородны. Постоянная m называется массой тела. Масса является мерой инертности тела впоступательном движении. Чем меньше инертность тела, тем большее ускорение оно должно приобретать под действием какой-либо определенной силы. Таким образом, второй закон Ньютона можно сформулировать в следующем виде: ускорение тела прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела.
Принцип независимости действия сил
Если на материальную точку действуют несколько сил, то
|
(3.3) |
где ![]() -
ускорение материальной точки, вызываемое
действием на нее одной силы
.
Таким образом, если на материальную
точку одновременно действуют несколько
сил, то каждая из них сообщает м.т. такое
же ускорение, как если бы других сил не
было. Это утверждение называется
принципом независимости действия сил.
-
ускорение материальной точки, вызываемое
действием на нее одной силы
.
Таким образом, если на материальную
точку одновременно действуют несколько
сил, то каждая из них сообщает м.т. такое
же ускорение, как если бы других сил не
было. Это утверждение называется
принципом независимости действия сил.
Третий закон Ньютона формулируется следующим образом:
Две материальные точки действуют друг на друга с силами, которые численно равны между собой и направлены во взаимно противоположные стороны вдоль прямой, соединяющей эти точки:
|
(3.4) |
Следует
отметить, что силы![]() и
и ![]() приложены
к разным телам и поэтому не уравновешивают
друг друга.
приложены
к разным телам и поэтому не уравновешивают
друг друга.
5Закон сохранения импульса и его применение. Центр масс
Простые
наблюдения и опыты доказывают, что покой
и движение относительны, скорость тела
зависит от выбора системы отсчета; по
второму закону Ньютона независимо от
того, находилось ли тело в покое или
двигалось, изменение скорости его
движения может происходить только под
действием силы, т. е. в результате
взаимодействия с другими телами. Однако
существуют величины, которые могут
сохраняться при взаимодействии тел.
Такими величинами являются энергия и
импульс.
Импульсом тела называют векторную
физическую величину, являющуюся
количественной характеристикой
поступательного движения тел. Импульс
обозначается р. Импульс тела равен
произведению массы тела на его скорость:
р = mv. Направление вектора импульса р
совпадает с направлением вектора
скорости тела 0. Единица измерения
импульса — кг • м/с.
Для импульса системы тел выполняется
закон сохранения, который справедлив
только для замкнутых физических систем.
В общем случае замкнутой называют
систему, которая не обменивается энергией
и массой с телами и полями, не входящими
в нее. В механике замкнутой называют
систему, на которую не действуют внешние
силы или действие этих сил скомпенсировано.
В этом случае p1 = р2, где pl — начальный
импульс системы, а р2 — конечный. В случае
двух тел, входящих в систему, это выражение
имеет вид m1v1 + m2v2 = m1"v1" + m2"v2" ,
где ml и m2 — массы тел, а v1 и v2 — скорости
до взаимодействия, v1" и v2" — скорости
после взаимодействия (рис.
5).
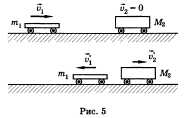 Эта формула и является математическим
выражением закона сохранения импульса:
импульс замкнутой физической системы
сохраняется при любых взаимодействиях,
происходящих внутри этой системы.
Другими словами: в замкнутой физической
системе геометрическая сумма импульсов
тел до взаимодействия равна геометрической
сумме импульсов этих тел после
взаимодействия. В случае незамкнутой
системы импульс тел системы не сохраняется.
Однако если в системе существует
направление, по которому внешние силы
не действуют или их действие скомпенсировано,
то сохраняется проекция импульса на
это направление. Кроме того, если время
взаимодействия мало (выстрел, взрыв,
удар), то за это время даже в случае
незамкнутой системы внешние силы
незначительно изменяют импульсы
взаимодействующих тел. Поэтому для
практических расчетов в этом случае
тоже можно применять закон сохранения
импульса.
Экспериментальные исследования
взаимодействий различных тел — от
планет и звезд до атомов и элементарных
частиц — показали, что в любой системе
взаимодействующих тел при отсутствии
действия со стороны других тел, не
входящих в систему, или равенстве нулю
суммы действующих сил геометрическая
сумма импульсов тел действительно
остается неизменной.
В механике закон сохранения импульса
и законы Ньютона связаны между собой.
Если на тело массой т в течение времени
t действует сила и скорость его движения
изменяется от v0 до v, то ускорение движения
а тела равно
Эта формула и является математическим
выражением закона сохранения импульса:
импульс замкнутой физической системы
сохраняется при любых взаимодействиях,
происходящих внутри этой системы.
Другими словами: в замкнутой физической
системе геометрическая сумма импульсов
тел до взаимодействия равна геометрической
сумме импульсов этих тел после
взаимодействия. В случае незамкнутой
системы импульс тел системы не сохраняется.
Однако если в системе существует
направление, по которому внешние силы
не действуют или их действие скомпенсировано,
то сохраняется проекция импульса на
это направление. Кроме того, если время
взаимодействия мало (выстрел, взрыв,
удар), то за это время даже в случае
незамкнутой системы внешние силы
незначительно изменяют импульсы
взаимодействующих тел. Поэтому для
практических расчетов в этом случае
тоже можно применять закон сохранения
импульса.
Экспериментальные исследования
взаимодействий различных тел — от
планет и звезд до атомов и элементарных
частиц — показали, что в любой системе
взаимодействующих тел при отсутствии
действия со стороны других тел, не
входящих в систему, или равенстве нулю
суммы действующих сил геометрическая
сумма импульсов тел действительно
остается неизменной.
В механике закон сохранения импульса
и законы Ньютона связаны между собой.
Если на тело массой т в течение времени
t действует сила и скорость его движения
изменяется от v0 до v, то ускорение движения
а тела равно ![]() Ha
основании второго закона Ньютона для
силы F можно записать
Ha
основании второго закона Ньютона для
силы F можно записать ![]() ,
отсюда следует
,
отсюда следует
![]() Ft — векторная физическая величина,
характеризующая действие на тело силы
за некоторый промежуток времени и равная
произведению силы на время ее действия,
называется импульсом силы. Единица
импульса силы в СИ — Н*с.
Закон сохранения импульса лежит в основе
реактивного движения. Реактивное
движение — это такое движение тела,
которое возникает после отделения от
тела его части.
Пусть тело массой т покоилось. От тела
отделилась со скоростью vl какая-то его
часть массой т1. Тогда оставшаяся часть
придет в движение в противоположную
сторону со скоростью D2, масса оставшейся
части т2. Действительно, сумма импульсов
обеих частей тела до отделения была
равна нулю и после разделения будет
равна нулю:
Ft — векторная физическая величина,
характеризующая действие на тело силы
за некоторый промежуток времени и равная
произведению силы на время ее действия,
называется импульсом силы. Единица
импульса силы в СИ — Н*с.
Закон сохранения импульса лежит в основе
реактивного движения. Реактивное
движение — это такое движение тела,
которое возникает после отделения от
тела его части.
Пусть тело массой т покоилось. От тела
отделилась со скоростью vl какая-то его
часть массой т1. Тогда оставшаяся часть
придет в движение в противоположную
сторону со скоростью D2, масса оставшейся
части т2. Действительно, сумма импульсов
обеих частей тела до отделения была
равна нулю и после разделения будет
равна нулю:
![]() Большая
заслуга в развитии теории реактивного
движения принадлежит К. Э.
Циолковскому.
Он разработал теорию полета тела
переменной массы (ракеты) в однородном
поле тяготения и рассчитал запасы
топлива, необходимые для преодоления
силы земного притяжения; основы теории
жидкостного реактивного двигателя, а
также элементы его конструкции; теорию
многоступенчатых ракет, причем предложил
два варианта: параллельный (несколько
реактивных двигателей работают
одновременно) и последовательный
(реактивные двигатели работают друг за
другом). К. Э. Циолковский строго научно
доказал возможность полета в космос с
помощью ракет с жидкостным реактивным
двигателем, предложил специальные
траектории посадки космических аппаратов
на Землю, выдвинул идею создания
межпланетных орбитальных станций и
подробно рассмотрел условия жизни и
жизнеобеспечения на них. Технические
идеи Циолковского находят применение
при создании современной ракетно-космической
техники. Движение с помощью реактивной
струи по закону сохранения импульса
лежит в основе гидрореактивного
двигателя. В основе движения многих
морских моллюсков (осьминогов, медуз,
кальмаров, каракатиц) также лежит
реактивный принцип.
Большая
заслуга в развитии теории реактивного
движения принадлежит К. Э.
Циолковскому.
Он разработал теорию полета тела
переменной массы (ракеты) в однородном
поле тяготения и рассчитал запасы
топлива, необходимые для преодоления
силы земного притяжения; основы теории
жидкостного реактивного двигателя, а
также элементы его конструкции; теорию
многоступенчатых ракет, причем предложил
два варианта: параллельный (несколько
реактивных двигателей работают
одновременно) и последовательный
(реактивные двигатели работают друг за
другом). К. Э. Циолковский строго научно
доказал возможность полета в космос с
помощью ракет с жидкостным реактивным
двигателем, предложил специальные
траектории посадки космических аппаратов
на Землю, выдвинул идею создания
межпланетных орбитальных станций и
подробно рассмотрел условия жизни и
жизнеобеспечения на них. Технические
идеи Циолковского находят применение
при создании современной ракетно-космической
техники. Движение с помощью реактивной
струи по закону сохранения импульса
лежит в основе гидрореактивного
двигателя. В основе движения многих
морских моллюсков (осьминогов, медуз,
кальмаров, каракатиц) также лежит
реактивный принцип.
ЦЕНТР МАСС
В
любой системе частиц имеется одна
замечательная точка С- центр
инерции,
или центр
масс,
- которая обладает рядом интересных и
важных свойств. Центр масс является
точкой приложения вектора импульса
системы ![]() ,
так как вектор любого импульса является
полярным вектором. Положение
точки С относительно
начала О данной
системы отсчета характеризуется
радиусом-вектором, определяемым следующей
формулой:
,
так как вектор любого импульса является
полярным вектором. Положение
точки С относительно
начала О данной
системы отсчета характеризуется
радиусом-вектором, определяемым следующей
формулой:
|
(4.8) |
где ![]() -
масса и радиус-вектор каждой частицы
системы, M -
масса всей
-
масса и радиус-вектор каждой частицы
системы, M -
масса всей
системы (рис. 4.3).
|
Рис. 4.3. Определение центра масс системы частиц |
Следует заметить, что центр масс системы совпадает с ее центром тяжести. Правда, это утверждение справедливо лишь в том случае, когда поле сил тяжести в пределах данной системы можно считать однородным.
Найдем скорость центра масс в данной системе отсчета. Продифференцировав (4.8) по времени, получим
|
(4.9) |
Если
скорость центра инерции равна нулю, то
говорят, что система как целое покоится.
Это вполне естественное обобщение
понятия покоя отдельной частицы. Скорость
же ![]() приобретает
смысл скорости движения системы как
целого.
приобретает
смысл скорости движения системы как
целого.
Из формулы (4.9) с учетом (4.3) следует, что
|
(4.10) |
т.е. импульс системы равен произведению массы системы на скорость ее центра масс.
Получим уравнение движения центра масс. Понятие центра масс позволяет придать уравнению (4.4) иную форму, которая часто оказывается более удобной. Для этого достаточно(4.10) подставить в (4.4), и учесть, что масса системы как таковой есть величина постоянная. Тогда получим
|
(4.11) |
где ![]() -
результирующая всех внешних сил,
действующих на систему. Это и есть уравнение
движения центра масс системы
- одно из важнейших уравнений механики.
В соответствии с этим уравнением, при
движении любой системы частиц ее центр
инерции движется так, как если бы вся
масса системы была сосредоточена в этой
точке и к ней были бы приложены все
внешние силы,
действующие на систему. При этом ускорение
центра инерции совершенно не зависит
от точек приложения внешних сил.
-
результирующая всех внешних сил,
действующих на систему. Это и есть уравнение
движения центра масс системы
- одно из важнейших уравнений механики.
В соответствии с этим уравнением, при
движении любой системы частиц ее центр
инерции движется так, как если бы вся
масса системы была сосредоточена в этой
точке и к ней были бы приложены все
внешние силы,
действующие на систему. При этом ускорение
центра инерции совершенно не зависит
от точек приложения внешних сил.
Далее,
из уравнения (4.11) следует,
что если ![]() то
то ![]() а
значит,
а
значит, ![]() .
В инерциальной системе отсчета такой
случай реализуется для замкнутой
системы. Кроме того, если
,
то, согласно (4.10);
и импульс системы
.
В инерциальной системе отсчета такой
случай реализуется для замкнутой
системы. Кроме того, если
,
то, согласно (4.10);
и импульс системы ![]() .
.
Таким образом, если центр масс системы движется равномерно и прямолинейно, то это означает, что ее импульс сохраняется в процессе движения. Разумеется, справедливо и обратное утверждение.
Уравнение (4.11). по форме совпадает с основным уравнением динамики материальной точки и является его естественным обобщением на систему частиц: ускорение системы как целого пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы. Напомним, что в неинерциальных системах отсчета результирующая всех внешних сил включает в себя как силы взаимодействия с окружающими телами, так и силы инерции.
Рассмотрим ряд примеров на движение центра масс системы.
Пример 1. Покажем, как можно решить задачу с человеком на плоту (стр. 90 )другим способом, воспользовавшись понятием центра масс.
Так как сопротивление воды пренебрежимо мало, то результирующая всех внешних сил, действующих на систему человек - плот, равна нулю. А это значит, что положение центра инерции данной системы в процессе движения человека (и плота) меняться не будет, т. е.
![]() .
.
где ![]() и
и ![]() -
радиус-векторы, характеризующие положения
центров масс человека и плота относительно
некоторой точки берега. Из этого равенства
найдем связь между приращениями
векторов
и
-
радиус-векторы, характеризующие положения
центров масс человека и плота относительно
некоторой точки берега. Из этого равенства
найдем связь между приращениями
векторов
и
![]()
![]()
Имея
в виду, что приращения ![]() и
представляют собой перемещения человека
и плота относительно берега, найдем
перемещение плота:
и
представляют собой перемещения человека
и плота относительно берега, найдем
перемещение плота:
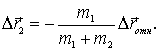
Пример
2. Человек прыгает с вышки в воду. Движение
прыгуна в общем случае имеет весьма
сложный характер. Однако если сопротивление
воздуха пренебрежимо мало, то можно
сразу утверждать, что центр инерции
прыгуна движется по параболе, как
материальная точка, на которую действует
постоянная сила ![]() где
где ![]() масса
человека.
масса
человека.
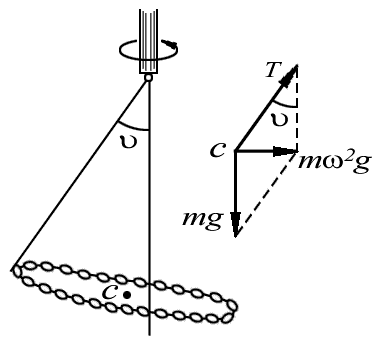
Пример
3. Замкнутая цепочка, соединенная нитью
с концом оси центробежной машины,
равномерно вращается вокруг вертикальной
оси с угловой скоростью ![]() (рис.
4.4). При этом нить образует угол
(рис.
4.4). При этом нить образует угол ![]() с
с
|
Рис. 4.4. Вращение цепочки вокруг вертикальной оси |
вертикалью. Как ведет себя центр инерции цепочки?
Прежде всего, ясно, что при равномерном вращении центр инерции цепочки не движется в вертикальном направлении. Это значит, что вертикальная составляющая силы Т натяжения нити компенсирует силу тяжести (рис. 4.4, справа). Горизонтальная же составляющая силы натяжения постоянна по модулю и все время направлена к оси вращения.
Отсюда
следует, что центр масс цепочки - точка
С - движется по горизонтальной окружности,
радиус которой ![]() легко
найти с помощью формулы (4.11),
записав ее в виде
легко
найти с помощью формулы (4.11),
записав ее в виде
![]()
где![]() -
масса цепочки. При этом точка С все время
находится между осью вращения и нитью,
как показано на рис. 4.4.
-
масса цепочки. При этом точка С все время
находится между осью вращения и нитью,
как показано на рис. 4.4.
В тех часто встречающихся случаях, когда нас интересует лишь относительное движение частиц внутри системы, а не движение этой системы как целого, наиболее целесообразно пользоваться системой отсчета, в которой центр масс покоится. Это позволяет значительно упростить и анализ явления и расчеты.
Систему отсчета, жестко связанную с центром масс данной системы частиц и перемещающуюся поступательно по отношению к инерциальным системам, называют системой центра масс или, кратко, С-системой (обозначение системы связано с первой буквой слова центр по латыни). Отличительной особенностью этой системы является то, что полный импульс системы частиц в ней равен нулю - это непосредственно следует из формулы (4.10). Другими словами, любая система частиц как целое покоится в своей -С-системе.
Для замкнутой системы частиц ее С-система является инерциальной, для незамкнутой - в общем случае неинерциальной.
Найдем
связь между значениями механической
энергии системы в K и С системах
отсчета. Начнем с кинетической энергии
системы ![]() .
Скорость
.
Скорость ![]() частицы
частицы ![]() в K-системе
можно представить в виде суммы
скоростей,
в K-системе
можно представить в виде суммы
скоростей, ![]() где
где ![]() и
и ![]() -
скорость этой частицы в С-системе
и скорость системы центра масс
относительно K-системы
отсчета соответственно. Тогда можно
записать:
-
скорость этой частицы в С-системе
и скорость системы центра масс
относительно K-системы
отсчета соответственно. Тогда можно
записать:
![]() .
.
Так как в С-системе среднее слагаемое в последней сумме равно 0, то предыдущее выражение примет вид
|
(4.12) |
где ![]() -
суммарная кинетическая энергия частиц
в С-системе, масса всей системы
обозначена
-
суммарная кинетическая энергия частиц
в С-системе, масса всей системы
обозначена ![]() а
а ![]() -
ее полный импульс в K-системе отсчета.
-
ее полный импульс в K-системе отсчета.
Таким образом, кинетическая энергия системы частиц складывается из суммарной кинетической энергии в С-системе и кинетической энергии, связанной с движением системы частиц как целого. Это важный вывод, который неоднократно будет использоваться в дальнейшем изложении.
Из формулы (4.12) следует, что кинетическая энергия системы частиц минимальна в С-системе - в этом еще одна особенность С-системы. Действительно, в С-системе импульс системы равен 0 и поэтому в (4.12) остается только .
Теперь перейдем к полной механической энергии Е. Так как собственная потенциальная энергия системы U зависит только от конфигурации системы, т.е. относительного взаимного расположения частей, то значение U одинаково во всех системах отсчета в соответствии с принципом относительности Галилея. Добавив U в левую и правую части равенства (4.12), получим формулу преобразования полной механической энергии при переходе от К к С-системе:
|
(4.13) |
Энергию ![]() ,
равную сумме потенциальной энергии и
кинетической энергии системы в С-системе
называют внутренней
механической энергией системы.
,
равную сумме потенциальной энергии и
кинетической энергии системы в С-системе
называют внутренней
механической энергией системы.
Пример.
На гладкой горизонтальной плоскости
лежат две небольшие шайбы, каждая
массы
,
которые соединены между собой невесомой
пружинкой. Одной из шайб сообщили
начальную скорость ![]() как
показано на рис. 4.5. Какова внутренняя
механическая энергия
этой
системы в процессе движения?
как
показано на рис. 4.5. Какова внутренняя
механическая энергия
этой
системы в процессе движения?
Поскольку
плоскость гладкая, система в процессе
движения будет вести себя как замкнутая.
Поэтому ее полная механическая энергия ![]() и
и
|
Рис. 4.5. Пример на внутреннюю механическую энергию системы |
суммарный
импульс ![]() будут
сохраняться, оставаясь равными тем
значениям, которые они имели в начальный
момент, т. е.
будут
сохраняться, оставаясь равными тем
значениям, которые они имели в начальный
момент, т. е. ![]() .
Подставив эти значения в формулу (4.13),
получим
.
Подставив эти значения в формулу (4.13),
получим
![]()
Нетрудно сообразить, что внутренняя энергия связана с вращением и колебанием данной системы, причем в начальный момент была равна только энергии вращательного движения.
Если
система частиц замкнута и
в ней происходят процессы, связанные с
изменением полной механической энергии,
то из (4.13) следует,
что ![]() ,
т. е. приращение полной механической
энергии относительно произвольной
инерциальной системы отсчета равно
приращению внутренней механической
энергии. При этом кинетическая энергия,
обусловленная движением системы частиц
как целого, не меняется, ибо для замкнутой
системы полный импульс системы
сохраняется
,
т. е. приращение полной механической
энергии относительно произвольной
инерциальной системы отсчета равно
приращению внутренней механической
энергии. При этом кинетическая энергия,
обусловленная движением системы частиц
как целого, не меняется, ибо для замкнутой
системы полный импульс системы
сохраняется ![]() .
.
В частности, если замкнутая система консервативна, то ее полная механическая энергия сохраняется во всех инерциальных системах отсчета. Этот вывод находится в полном соответствии с принципом относительности Галилея.
Рассмотрим
простейшую систему из двух частиц. Пусть
их массы равны ![]() и
и ![]() ,
а их скорости в K-системе
отсчета соответственно равны
,
а их скорости в K-системе
отсчета соответственно равны ![]() и
и ![]() .
Найдем выражения, определяющие их
импульсы и суммарную кинетическую
энергию в С-системе.
.
Найдем выражения, определяющие их
импульсы и суммарную кинетическую
энергию в С-системе.
Импульс первой частицы в С-системе
![]()
где - скорость центра масс (С-системы) в K-системе отсчета. После подстановки в эту формулу выражения (4.9) для получим
![]()
где ![]() так
называемая приведенная
масса системы,
так
называемая приведенная
масса системы,
|
(4.14) |
Аналогично, импульс второй частицы в C-системе
![]()
Таким образом, импульсы обеих частиц в C-системе одинаковы по модулю и противоположны по направлению, причем модуль импульса каждой частицы
|
(4.15) |
где ![]() -
модуль скорости одной частицы относительно
другой.
-
модуль скорости одной частицы относительно
другой.
Рассмотрим теперь выражение для кинетической энергии. Суммарная кинетическая энергия обеих частиц в С-системе
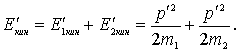
Так
как, согласно (4.14), ![]() ,
то
,
то
|
(4.16) |
Если частицы взаимодействуют друг с другом, то полная механическая энергия обеих частиц в C-системе записывается в виде
|
(4.17) |
где ![]() -
потенциальная энергия взаимодействия
данных частиц.
-
потенциальная энергия взаимодействия
данных частиц.
Выведенные формулы играют большую роль при изучении столкновения частиц, которое часто необходимо в ядерной физике.
6. Полная механическая энергия системы. Закон сохранения механической энергии. Работа силы.
Полная механическая энергия системы — это сумма ее потенциальной и кинетической энергий: E=Ek+Ep.
Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия
![]()
Тело
начало свободно падать ![]() .
Из кинематики известно, что момент
достижения поверхности земли оно будет
иметь скорость
.
Из кинематики известно, что момент
достижения поверхности земли оно будет
иметь скорость ![]() икинетическую
энергию:
икинетическую
энергию:
![]()
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:
![]()
На
поверхности Земли h=0 и потенциальная
энергия ![]() ,
а
,
а ![]() -максимальна.
В начале падения
-максимальна.
В начале падения ![]() ,
а
,
а![]() т.е.
потенциальная энергия переходит
(превращается) в кинетическую. Таким
образом, при падении тела в системе
тело-Земля кинетическая энергия
возрастает и, следовательно, ее
изменение
т.е.
потенциальная энергия переходит
(превращается) в кинетическую. Таким
образом, при падении тела в системе
тело-Земля кинетическая энергия
возрастает и, следовательно, ее
изменение ![]() равное
работе
равное
работе ![]() ,
имеет положительный знак, т.е.
,
имеет положительный знак, т.е.
|
(4.12) |
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
|
(4.13) |
Сложив (4.12) и (4.13), получим
![]()
или ![]()
Сумма ![]() представляет
собой полную энергию, и, следовательно,
представляет
собой полную энергию, и, следовательно,
![]() ,
а
,
а
|
(4.14) |
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.
Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.
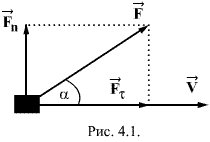
Если
рассматриваемая сила
постоянна,а
тело, к которому она приложена, движется
поступательно и прямолинейно, то работой,
совершаемой силой ![]() при
прохождении телом пути
при
прохождении телом пути ![]() ,
называют величину
,
называют величину
|
(4.1) |
где а - угол между силой и направлением движения тела.
Работа
- скалярная величина. Если вектор силы
и вектор перемещений образуют острый
угол т.е. ![]() ,
то
,
то ![]() ,
если
,
если ![]() ,
то
,
то ![]() ,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.
,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.
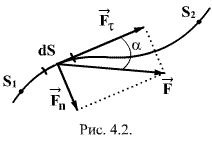
В
общем случае тело может двигаться
произвольным, достаточно сложным образом
(рис.4.2). Выделим элементарный участок
пути ![]() ,
на котором силу можно считать постоянной
и перемещение прямолинейным. Элементарная
работа на этом участке равна
,
на котором силу можно считать постоянной
и перемещение прямолинейным. Элементарная
работа на этом участке равна
|
(4.2) |
Полная
работа на пути ![]() определяется
интегралом
определяется
интегралом
|
(4.3) |
8Удар абсолютно упругих и неупругих тел.



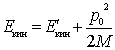

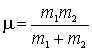 .
.