
Прямолинейная зависимость
Существует несколько способов определения прямой линии для выражения функционального отношения между двумя переменными. Из бесчисленного множества прямых линий, которые можно провести на плоскости, следует выбрать одну, наилучшим образом соответствующую нашим экспериментальным данным, т. е. определить параметры уравнения этой линии.
С такого рода задачами часто встречаются в аналитической работе. Например, при определении параметров градуировочного графика, который наилучшим образом соответствует результатам анализов, выполненных для серии эталонов.
Результаты этих анализов могут быть представлены системой уравнений

где хi — концентрация определяемого компонента в i-том эталоне;
уi — результаты прямых измерений, связанных с анализом i -того эталона;
а и b — параметры градуировочного графика.
В общем случае, мы имеем m уравнений для определения двух неизвестных величин а и b. Так как уi определяется с ошибкой, то нет ни одной системы значений а и b, которые бы строго удовлетворяли всем т уравнениям. Поэтому задача сводится к отысканию таких значений для параметров а и b, которые бы только наилучшим образом удовлетворяли всем уравнениям. В основе методики определения коэффициентов а и b лежит способ наименьших квадратов.
Способ наименьших квадратов сводится к определению параметров такой прямой, для которой сумма квадратов разностей между экспериментальными значениями и соответствующими значениями на прямой минимальна
![]() (3.25)
(3.25)
Заменив ух через а + bх, получим функцию от параметров а и b

Приравняв нулю первые производные по а и b от суммы квадратов отклонений, найдем значения а и b , удовлетворяющие минимуму функций

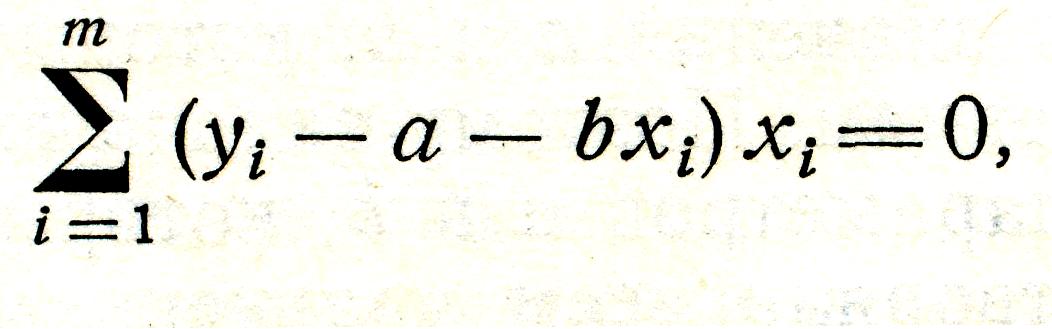
откуда
 (3.26)
(3.26)
Решая эти уравнения относительно а и b, находим:
 (3.27)
(3.27)
При вычислении параметров прямой линии данные располагают так, как это показано в табл. 3.8, в которой приведены результаты опробования восьми камер основной цинковой флотации.
Таблица 3.8
Расчет параметров прямой линии

Здесь ε - коэффициент скорости флотации Опробование проводилось в течение 4 смен. По результатам опробования определены значения коэффициента кинетики
![]()
в каждой камере для всех смен (см. табл.3.8, графы 2—5). Для систематизации полученных данных строим поле корреляции (см. рис.3.11). Расположение точек в корреляционном поле свидетельствует о наличии отчетливо выраженной зависимости между номером камеры к и коэффициентом кинетики у , т. е. между к и у. Точки, расположенные в левой части поля, оказываются ниже точек, расположенных справа: по мере увеличения абсцисс ординаты точек тоже увеличиваются. Определив средние значения ординат для каждой камеры (см. табл. 3.8, графу 6) и соединив их прямыми линиями, получим ломаную, представляющую собой эмпирическую линию регрессии.
Характер расположения точек на корреляционном поле нам подсказывает, что теоре-тическая линия регрессии является прямой. Для определения неизвестных параметров пря-
мой а
и b
подсчитываем
суммы
![]() и по формуле
(3.27) находим значения неиз-вестных а
и
b.
Отсюда
уравнение искомой
прямой
и по формуле
(3.27) находим значения неиз-вестных а
и
b.
Отсюда
уравнение искомой
прямой
![]()

Рис. 3.11. Экспериментальные (1) и расчетные (2) кривые зависимости
между временем флотации и коэффициентом кинетики
Придавая переменной х различные значения, получаем из уравнения соответствую-щие значения ух (см. табл.3.8, графу 9) для всех х, записанных в графе 1. По этим данным чертим прямую линию регрессии (см. рис. 3.11, прямая 2), которая может быть использована для приближенной оценки скорости флотации в любой из восьми камер флотации.
Выражение зависимости у =f(х), где символ f(х) обозначает подбираемую форму кри-вой, называется уравнением регрессии.
Если вычислить разности между фактическими наблюдениями и значениями, вычисленными по этому уравнению, возвести их в квадрат и суммировать, то сумма должна быть меньше, чем сумма квадратов разностей, получаемая для какой-либо другой прямой линии.
Каков физический смысл параметров уравнения (3.27) а = 0,062 и b = 0,021, вычисленных на основании выборки, состоящей из 32 наблюдений?
Значение а представляет собой ординату при x=0, т. е. величину ожидаемого извлечения до первой камеры, например в чане перемешивания. Но, поскольку в чане концентрат не снимают, такое утверждение представляется абсурдным. Коэффициент а, таким образом, не имеет значения сам по себе, представляя в данном примере лишь общее начало для отсчета тех отрезков ординат, в которые уже вложен определенный смысл. Показатель b, напротив, всегда имеет определенное смысловое значение. Он говорит о том, насколько в среднем для всех наблюдений изменяется у при изменении к на одну единицу. В нашем примере величина 0,021 означает, что при возрастании х на одну единицу, равную одной камере, скорость флотации, выраженная в
![]()
увеличивается на 0,021.
Криволинейная зависимость
Далеко не все зависимости могут быть хорошо выражены прямой линией. Иногда их правильнее представлять кривыми различных типов, например:

Выбор уравнения для различных совокупностей данных зависит от логического ана-лиза. С помощью многочленов достаточно высокого порядка можно воспроизвести значение произвольной функции внутри некоторого интервала.
Математическая формула, освобождающая эмпирический материал от случайных зиг-загов и позволяющая установить приближенно действительный тип зависимости, способ-ствует более глубокому проникновению в механизм действия факторов, обусловливающих эту зависимость.
Требование наименьших квадратов сохраняется и при расчете параметров криволи-нейной регрессии.
Для параболы
![]() (3.28)
(3.28)
параметры а, b и с определяются из соотношения
![]()
откуда после преобразований получаем
 (3.29)
(3.29)
Решая ее, находим искомые значения параметров а, b и с уравнения регрессии.
Таким образом, способ наименьших квадратов позволяет исследователю определить, каким образом происходят изменения значений одной переменной в связи с изменениями значений другой переменной.
Следует отметить, что независимо от того, хорошо или плохо подобрана формула, всякая попытка производить оценки вне пределов наблюдений путем экстраполяции может дать результат, который можно только логически предполагать. Статистический же анализ может указать на то, что имеется зависимость в пределах диапазона наблюдений, используемых для этого анализа, и только в пределах определенного доверительного интервала. В качестве примера на рис. 3.12 приведена нелинейная зависимость между временем старения реагента и его оптической плотностью.

Рис. 3.12. Экспериментальная (1) и расчетная (2) кривые зависимости между временем старения реагента и оптической
плотностью
Парная корреляция
Для характеристики тесноты связи между величинами х и у пользуются безразмерной величиной, называемой коэффициентом корреляции rху.
Коэффициент корреляции изменяется в пределах
-1<Гху<1.
Положительная корреляция между случайными величинами характеризует такую вероятностную зависимость между ними, когда при возрастании одной из них другая в среднем будет возрастать. Отрицательная корреляция характеризует такую зависимость, когда при возрастании одной случайной величины другая в среднем будет убывать. Величина коэффициента корреляции определяет тесноту связи между случайными величинами; чем ближе значение Гху к единице, тем теснее статистическая связь. Близкое к нулю значение коэффициента корреляции свидетельствует об отсутствии линейной связи.
О наличии или отсутствии связи между двумя случайными величинами в первом приближении судят по графику (корреляционному полю), на котором в виде точек изображены все полученные из опыта значения пар случайных величин. На рис. 3.13 приведены примеры случайных величин с положительной и отрицательной корреляцией.
Будем рассматривать двумерные наблюдения, т. е. такие наблюдения, которые дают значения двух случайных величин х и у. Допустим, что для обоих признаков х и у выполняется гипотеза нормальности. В этом случае говорят, что имеет место двумерное нормальное распределение. Нам нужно проверить гипотезу о наличии стохастической линейной связи между двумя случайными переменными x и у.

Рис. 3.13. Диаграммы рассеяния наблюдений при различных тесноте и видах связей между случайными величинами х и у:
а — тесная положительная связь; б — слабая отрицательная связь; в — отсутствие связи
Коэффициент корреляции rху определяется следующим образом:
![]()
 (3.30)
(3.30)
При вычислении коэффициента корреляции находят следующие суммы квадратов:
![]()
![]()
![]()
значения которых подставляют в формулу (3.30).
При вычислениях можно произвольным образом смещать начало отсчетов для обеих переменных. В табл.3.11 приведён пример расчета парного коэффициента корреляции.
Т аблица
3.11
аблица
3.11
Пример расчета парного коэффициента корреляции
В табл. 3.11 приведены данные по входному x и выходному y параметрам объекта исследования.
Определим коэффициент корреляции между этими факторами.
Расчеты становятся менее громоздкими, если каждое из чисел графы 1 уменьшить на 25, а числа графы 2 — на 8; полученные новые числа записаны в графах 3 и 4.
По полученным в таблице данным имеем:
![]()
![]()
![]()
так что коэффициент корреляции равен
![]()
Графы 8 и 9 служат для проверки правильности вычислений: должно выполняться равенство
![]()
В данном случае
![]()
что совпадает с
![]()
Не всякое значение коэффициента корреляции является достаточным для статистически обоснованных выводов о наличии корреляционной связи между исследуемыми переменными. Надежность статистических характеристик ослабевает с уменьшением объема выборки, а поэтому принципиально возможны случаи, когда отклонение от нуля полученной величины выборочного коэффициента корреляции оказывается статистически незначимым.
Связь можно считать достоверной, если
![]()
где |r | — абсолютное значение коэффициента корреляции;
t — коэффициент, соответствующий определенному уровню значимости (t — критерий);
Sr — среднеквадратичное отклонение коэффициента корреляции.
Средняя квадратичная ошибка коэффициента корреляции определяется по формуле
![]()
где п — число замеров.
Критерий надежности коэффициента корреляции рассчитывается как
![]()
Если μ>2,6, связь между переменными считается значимой.
Для оценки значимости коэффициентов корреляции можно также воспользоваться специальной таблицей.
Коэффициент корреляции имеет четкий смысл как характеристика тесноты связи между исследуемыми случайными величинами лишь в случае совместной нормальной распределенности исследуемых параметров. Во всех остальных случаях коэффициент корреляции можно признать лишь одной из возможных характеристик степени тесноты связи.
Кроме того, в случае нелинейной связи между переменными коэффициент корреляции также теряет свой смысл и для оценки связи используют корреляционное отношение

Для его вычисления необходимо найти следующие дисперсии:

—
средний квадрат отклонений (по ординате)
точек
корреляционного поля от линии
![]() = с;
= с;

— средний квадрат отклонений точек корреляционного поля от эмпирической линии регрессии;

— средний квадрат отклонений эмпирической
линии регрессии от линии = с.
Корреляционное отношение показывает, какая часть полной колеблемости у обусловлена изменчивостью аргумента х. Корень квадратный из величины η2 называется эмпирическим корреляционным отношением у по х.
Величина η2 (например, η2 = 0,55) свидетельствует, что дисперсия у, связанная с измен-чивостью х, составляет 55% полной дисперсии у. Следовательно, колеблемость выхода пара-метра для данного экспериментального материала на 55% обусловлена изменчивостью х и на 45% — влиянием прочих факторов, варьирующих независимо от х.
Вычисление корреляционного отношения позволяет решить вопрос, в какой мере соблю-дается строгая функциональная зависимость в изменении переменных у и х. Коэффициент корреляции, являющийся мерой, так называемой спрямленной зависимости переменных, имеет более узкий смысл, сохраняющийся независимо от того, прямолинейна или криволинейна действительная теоретическая линия регрессии у по х. Однако в первом случае коэффициент корреляции является одновременно и правильным измерителем тесноты корреляционной зави-симости. Во втором же случае величина коэффициента корреляции может оказаться значи-тельно меньше корреляционного отношения, рассчитанного в предположении криволинейной зависимости, если последняя сильно искажается в результате ее замены прямой линией.
Измерение связи между переменными обычно начинают с вычисления коэффициента корреляции. Так как даже в случае криволинейной зависимости он характеризует степень при-ближения корреляционной зависимости к функциональной зависимости и дает ориентировочное представление о тесноте корреляционной зависимости.
Используя коэффициент корреляции, кроме того, легко рассчитать параметры прямой линии регрессии у по х
![]()
Это осуществляется с помощью формул

![]()
Рассчитаем параметры линейной регрессии для следующих данных:
![]() =
104,16;
=107,62;
Sx=24,26;
SУ
=23,12; rуx
= 0,653.
=
104,16;
=107,62;
Sx=24,26;
SУ
=23,12; rуx
= 0,653.
Откуда получим:
![]()
![]()
![]()
Следует отметить, что к одному парному ряду наблюдений могут быть подобраны две линии регрессии
![]()
![]()
и один коэффициент корреляции, имеющий определенное отношение к обеим линиям регрессии. Коэффициент показывает, насколько эти линии приближаются одна к другой. Чем теснее корреляции, тем ближе две линии друг к другу, чем слабее — тем больше они расходятся.
Величина коэффициента корреляции может быть вычислена по угловому коэффициенту двух линий
![]()
Из этого уравнения следует, что когда r=1,
![]()
и, следовательно, обе линии регрессии совпадают; при r = 0 эти линии располагаются под прямым углом одна к другой.
Это свойство двух линий регрессии может быть использовано для оценки тесноты корреляционной связи графически.
Множественная регрессия
При изучении корреляции трех переменных одна из них рассматривается как функция, две другие — как аргументы. При нахождении поверхности множественной регрессии ограничимся предположением, что эта регрессия линейная, вида
![]() . (3.31)
. (3.31)
С геометрической точки зрения это уравнение определяет плоскость в пространстве переменных Х1, Х2, У. Расчет параметров а, b и с производим по способу наименьших квадратов. Необходимо, чтобы сумма квадратов отклонений фактических уi от Yi, вычисленных по уравнению регрессии, была наименьшей
![]()
Формула множественной регрессии с тремя переменными имеет следующий вид:
![]()
Коэффициенты b1 и b2 множественной регрессии находятся из системы линейных уравнений

где приняты следующие обозначения:
![]()
![]()
![]()
Следует отметить физический смысл коэффициентов множественной регрессии. Например, коэффициент b1 отвечает на вопрос, на сколько единиц в среднем изменяется Y, если X1 изменяется на одну единицу в предположении, что X2 при этом сохраняет постоянное значение.
Для оценки тесноты связи между несколькими переменными применяют коэффициент множественной корреляции R. Так для трех переменных он равен
 (3.32)
(3.32)
Из формулы ясно, что R≥ ryx1 и R≥ ryx2 , всегда положителен и находится в пределах от 0 до 1. Множественная регрессия применима к анализу любого числа переменных, однако объем вычислений с увеличением числа переменных резко возрастает.
Частная корреляция и частная регрессия
Методы частной корреляции и регрессии позволяют установить взаимные зависимости для группы переменных и показать, как связана между собой любая пара из них, если исключить влияние остальных переменных.
Общая формула для вычисления частных коэффициентов корреляции имеет такой вид:
 (3.33)
(3.33)
Здесь три переменные занумерованы числами 1, 2 и 3. Наша задача состоит в том, чтобы определить корреляцию между переменными 1 и 2 при исключении переменной 3. Это будет частная корреляция между 1 и 2. Соответствующий коэффициент частной корреляции обозначается r 12.3, где дается указание на исключение переменной 3. Символы r12, r13 и r23 относятся к корреляциям, определяемым непосредственно между каждой парой переменных.
Такие же коэффициенты r13.2 и r23.1 легко получить перестановкой индексов.
Для примера рассмотрим парные коэффициенты корреляции:
ryx1 = 0,3673; ryx2 = 0,5409 и rx2x1 = 0,2504.
Частные коэффициенты корреляции равны


При четырех переменных можно сначала исключить переменную 4 путем трехкратного применения приведенной выше формулы для определения r12.4, r13.4 и r23.4. Применяя эту же самую формулу снова к трем коэффициентам, получим
 (3.34)
(3.34)
Следует отметить, что объем вычислений очень быстро возрастает по мере увеличения числа исключаемых переменных.
Ограничимся пока рассмотрением пары независимых переменных x1 и x2. Согласно обоб-щенной концепции регрессионного анализа предположим, что для любой заданной пары зна-чений x1 и x2. измерения у имеют нормальное распределение с некоторым генеральным сред-ним значением (скажем, μx1x2) и дисперсией σ2, не зависящей от обеих переменных х1 и x2 , что генеральное среднее значение у можно выразить через х1 и x2 при помощи приближен-ного уравнения регрессии в виде
![]() (3.35)
(3.35)
Величины b1 и b2 есть соответственно частные коэффициенты регрессии у относи-тельно х1 и у относительно х2. Это простейшая применяемая на практике математическая модель.
