МИНИСТЕРСТВО ОБРАЗОВАНИЯ Российской Федерации

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

В.М.Шаповалов

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ ПРОЦЕССОВ ПЕРЕНОСА

Учебное пособие

РПК "Политехник"

Волгоград 2000

УДК 62-50:54+66(075)

Рецензенты: А.Ф.Крюков, В.В.Староверов

Шаповалов В.М. Лабораторный практикум по математическому моделированию процессов переноса: Учебное пособие/ВолгГТУ,Волгоград,2000.- 49 с.

ISBN 5-230-03812-8

Представлено подробное описание лабораторных установок в соответствии с последовательностью изучаемого теоретического курса и практических занятий по математическому моделированию процессов переноса. Структура и методическое содержание пособия соответствует разделам программы. Для отдельных задач даны математические модели процессов переноса тепла, массы. Уделено внимание простоте, наглядности и доступности экспериментальной части работ. Автор признателен сотрудникам кафедры Леонидовой С.А. и Харитонову В.Н. за выполнение иллюстраций.

Учебное пособие предназначено для студентов дневной формы обучения по направлению 5518 “Технологические машины и оборудование”.

Ил. 7. Табл.1. Библиогр: 10 назв.

Печатается по решению редакционно-издательского совета

Волгоградского государственного технического университета.

 Волгоградский

государственный

технический

университет,2000

Работа №1

Исследование процесса слива жидкости из сосуда

1. Цель работы: экспериментальная проверка расчетных формул продолжительности слива маловязких и высоковязких жидкостей из призматического сосуда.

2. Содержание работы.

1. Изучить применение закона Бернулли для анализа процесса слива маловязкой жидкости.

2. Учет влияния сил вязкого трения на продолжительность слива.

3. Зависимость коэффициента расхода от числа Рейнольдса.

4. Экспериментально определить продолжительность слива.

3. Теоретическая часть.

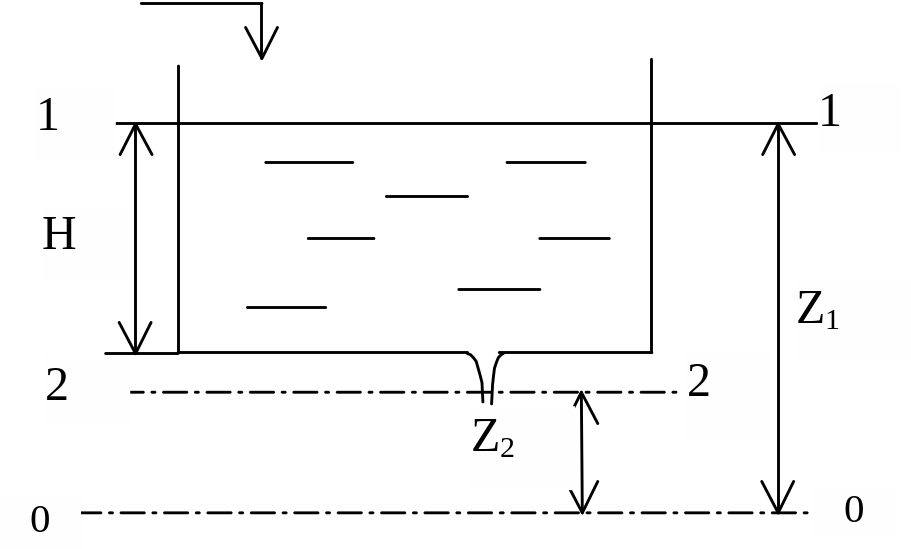
Определим расход маловязкой жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уровень H жидкости (рис. 1, а).

а б

Рис. 1. Истечение жидкости из сосуда:

а – при постоянном уровне; б – при переменном уровне.

Выбрав плоскость сравнения 0-0 параллельной днищу сосуда, напишем уравнение Бернулли (считая жидкость идеальной) для сечения 1-1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2-2, плоскость которого проходит через самое узкое сечение вытекающей струи

.

Для открытого сосуда ; кроме того, при постоянном уровне жидкости скорость ее . Пренебрегая небольшим расстоянием самого узкого сечения струи от дна, можно принять, что . Отсюда

.

Получим формулу Торичелли для идеальной жидкости

.

Скорость истечения жидкости не зависит от формы сосуда, а определяется только высотой столба жидкости над отверстием.

При истечении реальной жидкости часть напора Н теряется на трение и преодоление сопротивления, обусловленного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости

где  поправочный коэффициент ( <1), называемый коэффициентом скорости, который учитывает потери напора при истечении через отверстие.

Кроме того, вследствие сжатия струи на выходе из отверстия от сечения S₀ до S₂, скорость w₀ жидкости в отверстии должна быть меньше, чем w₂. Тогда

, ( 1 )

где  коэффициент сжатия струи,  коэффициент расхода. Коэффициент расхода определяют опытным путем, его значение зависит от критерия Re.

Объемный расход жидкости V_сек равен произведению ее скорости на площадь сечения S₀ отверстия

( 2 )

Из уравнения ( 2 ) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты уровня жидкости над отверстием и размера отверстия, но не зависит от формы сосуда. Это уравнение применимо также для определения расхода жидкости, вытекающей через отверстие в тонкой боковой стенке сосуда, если считать Н расстоянием от верхнего уровня жидкости до оси отверстия.

Для жидкостей, по вязкости мало отличающихся от воды, можно принять в первом приближении . При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнительная потеря напора на входе и выходе жидкости, что приводит к снижению . Вместе с тем, струя при входе в патрубок после некоторого сжатия снова расширяется и вытекает, заполняя все его сечение, т.е. можно считать . В итоге, коэффициент расхода жидкости при истечении через насадок оказывается большим, чем при истечении через отверстие, и для воды может быть принят .

Теперь рассмотрим истечение через отверстие в тонком днище при переменном уровне жидкости в сосуде, с целью определения времени опорожнения сосуда.

При таком истечении жидкости (рис. 1,б) ее уровень Н снижается во времени и, согласно уравнению ( 1 ), уменьшается также скорость истечения . Следовательно, процесс истечения носит нестационарный характер.

Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты Н₁ до некоторой высоты Н₂ . За бесконечно малый промежуток времени , в соответствии с уравнением ( 2 ), через отверстие в днище вытекает элементарный объем жидкости

где  площадь поперечного сечения отверстия.

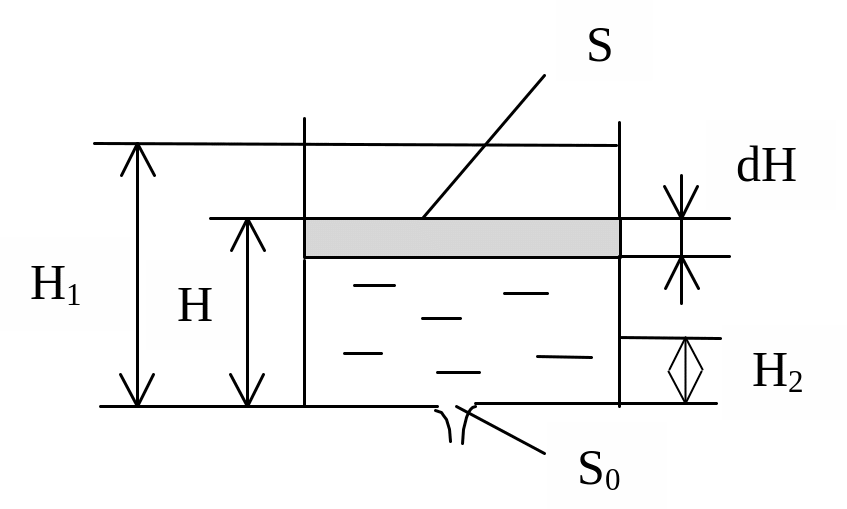
За тот же промежуток времени уровень жидкости в сосуде понизится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S сосуда убыль жидкости в нем составит

.

Знак минус указывает на уменьшение высоты жидкости в сосуде с ростом времени.

Приравнивая, согласно уравнению неразрывности потока, эти объемы, получаем дифференциальное уравнение первого порядка

откуда, разделяя переменные, имеем

(3)

Проинтегрируем это выражение для начального условия  ₁, принимая, что коэффициент расхода постоянен, т.е. не зависит от скорости истечения:

,

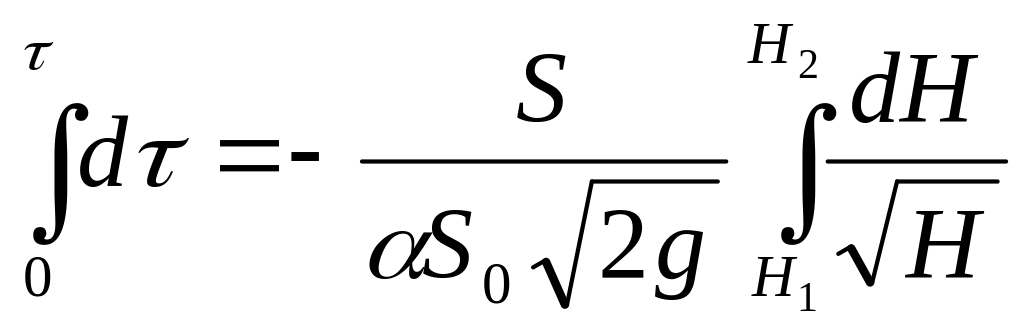выполнив интегрирование степенной функции в правой части, находим время

.

Таким образом, время опорожнения сосуда, имеющего постоянное поперечное сечение, от высоты H₁ до высоты H₂ составляет

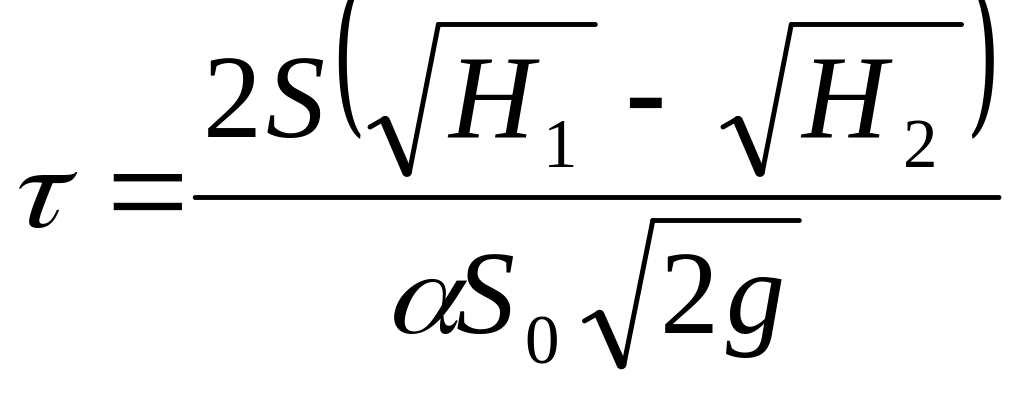. (4)

В случае полного опорожнения резервуара H₂ = 0 и уравнение ( 4 ) принимает вид

. (5)

При решении задачи о времени опорожнения сосуда, площадь поперечного сечения которого изменяется по высоте (например, при истечении из конических резервуаров, цистерны и др.) в процессе интегрирования должна быть учтена зависимость площади сечения S от уровня H жидкости.

Рассмотрим сосуд конической формы, расчетная схема которого представлена на рис.2.

Первоначальный уровень жидкости H₁ . Соответствующий диаметр свободной поверхности D₁. На текущей высоте H диаметр сосуда D. Требуется найти время истечения, т.е. время, по истечении которого уровень жидкости будет составлять H₂, а диаметр сосуда D₂ – соответственно.

Предварительно найдем зависимость D(H). Из условия геометрического подобия прямоугольных треугольников, можем записать

где x – неизвестное расстояние от дна сосуда до вершины конуса.

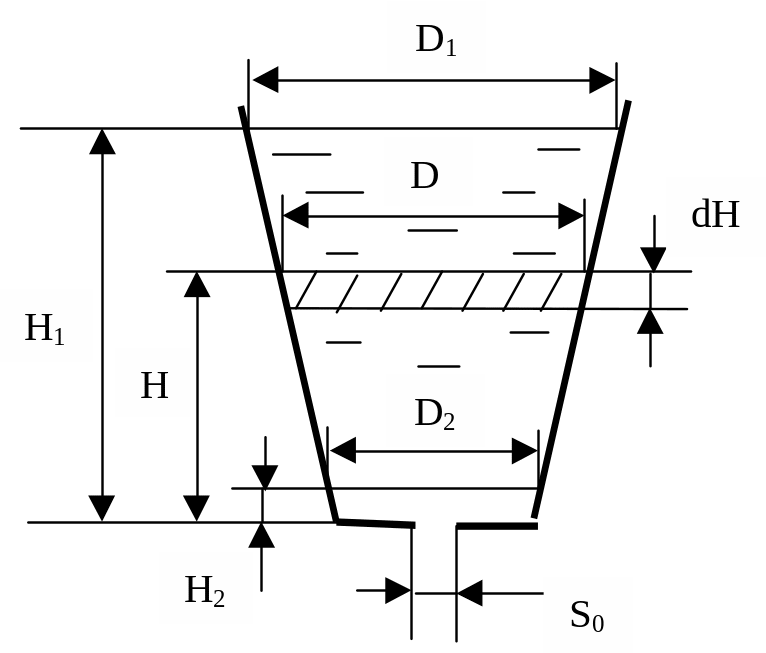
Рис.2. Схема слива жидкости из конического сосуда

Из первого равенства находим x

.

Далее из первого и последнего выражения с учетом x, получим для D линейную зависимость

Найдем площадь сечения сосуда для текущей высоты, т.е. функцию S(H)

.

Подставив это выражение в дифференциальное уравнение (3) и проинтегрировав его левую часть, можем записать

.

Учитывая , что

,

а также используя формулу Лейбница для определенных интегралов, имеем

В случае полного слива жидкости H₂=0 расчетное уравнение упрощается

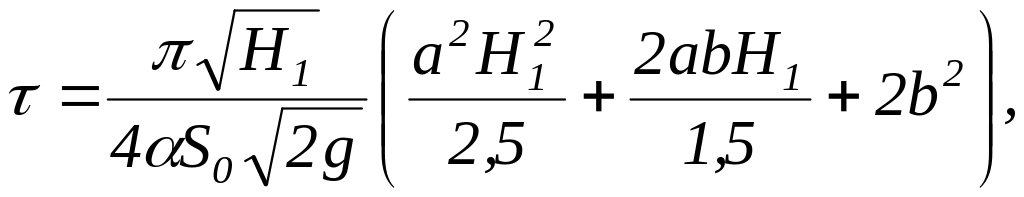( 6 )

Полученные расчётные зависимости пригодны исключительно для маловязких жидкостей, когда силы вязкого трения незначительны и справедливо исходное уравнение Бернулли.

Рассмотрим истечение жидкости значительной вязкости при переменном уровне. При выводе формулы ( 4 ) использовалось допущение const , т.е. коэффициент расхода принимался не зависящим от напора. В действительности коэффициент расхода зависит от числа Рейнольдса , где d – диаметр отверстия, а следовательно и от напора. В широком диапазоне значений коэффициент расхода изменяется незначительно, поэтому, используя формулу (4) или (5), при среднем значении 0,635 не следует ожидать значительной погрешности. При Re<50, т.е. при истечении жидкостей большой вязкости, коэффициент расхода с уменьшением Re начинает падать; в подобных случаях допущение const , а следовательно и формула (4), не дают правильных результатов. Для малых Re примем следующую зависимость для коэффициента расхода

. (7)

Рассмотрим истечение жидкости из отверстия в дне вертикального призматического сосуда при отсутствии притока (рис. 1,б). Используя, как получено выше, условие равенства элементарных расходов за время , дифференциальное уравнение (3) и формулу для (7), можем записать.

.

Проинтегрируем это выражение в пределах от H₁ до H₂ (используя начальное условие ₁)

.

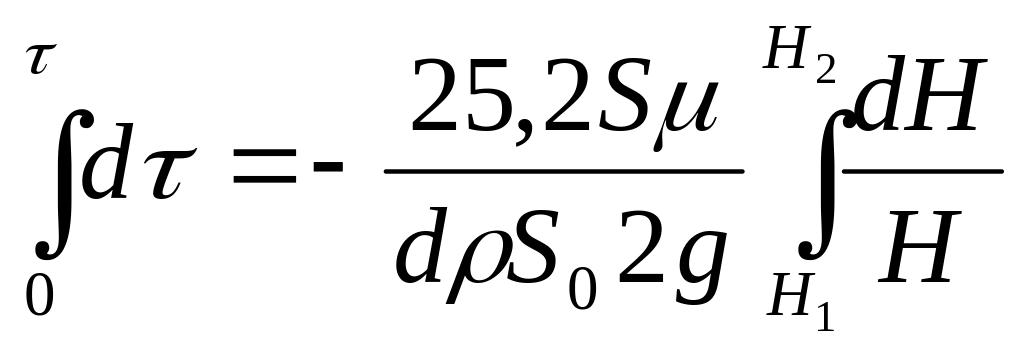В результате для времени истечения имеем

.

Или для цилиндрического сосуда, диаметром D, и круглого отверстия

. (8)

Уравнение (8) в отличие от уравнения (4) учитывает влияние вязкости жидкости на продолжительность истечения; из (8) следует, что время истечения прямо пропорционально вязкости. Из формулы ( 7 ) следует, что время полного опорожнения призматических сосудов стремиться к бесконечности ( ).

В случае, если давление на свободной поверхности жидкости больше атмосферного (для закрытого сосуда), формула (8) принимает вид

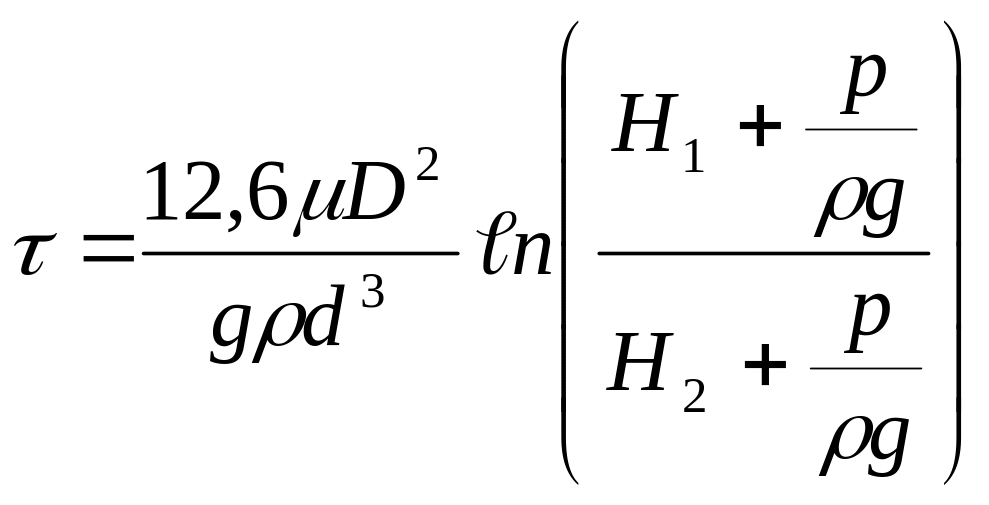, (9)

где p – избыточное давление на поверхности жидкости в сосуде. Из этой формулы следует, что время истечения жидкостей большой вязкости можно сократить, повышая избыточное давление или снижая её вязкость.

Пределы применимости уравнений (8), (9) определяются пределами применимости исходного уравнения ( 7 ), которое справедливо при условии

. (10)

Видно, что ограничения накладываются на напор H, а именно, его максимальное значение. При очень малых напорах ( <2) заметное влияние получают силы тяжести (подток жидкости по дну к отверстию, прорыв воздухом воронки), и уравнение ( 7 ), а следовательно, и формула ( 8 ) не дают правильных результатов.