3.3. Экономическая интерпретация переменных двойственной задачи

Запишем основную и двойственную задачи.

Исходная задача	Двойственная задача
при ограничениях	при ограничениях

Условия исходной задачи интерпретируем следующим образом. Надо планировать объем производства некоторого предприятия, имеющего ресурсы S_i в объемах b_i.

В задаче а_ij соответствует расходу сырья i-го вида на изготовление продукции вида j; с_j – величина прибыли, приходящаяся на единицу продукции j-го вида.

И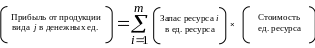 спользуем равенство значений целевых функций двух задач и проанализируем формулу с точки зрения размерностей входящих в нее величин.

Очевидно, что переменные двойственной задачи y_i представляют ценность единицы ресурса i. Их называют учетными, неявными, теневыми ценами.

Таким образом, задачи двойственной пары могут быть сформулированы так:

Исходная задача. Найти количество единиц x_j каждого вида продукции, которое нужно выпустить при данном доходе c_j от единицы продукции j-го вида и данном предельном потреблении каждого из имеющихся ресурсов b_i , чтобы получить от всего производства максимальную прибыль.

Двойственная задача. Какую цену y_i следует назначить единице каждого из ресурсов b_i для минимизации общей стоимости затрат на производство.

Двойственные оценки могут быть использованы для определения приоритета используемых ресурсов в величине целевой функции .

В примере исходная задача интерпретировалась как задача о сырье (частный случай задачи о ресурсах).

Мы получили Это значит, что значимость первого ресурса не высока, увеличение запаса только этого сырья не увеличит прибыли. Большее значение имеют второй и третий виды сырья.

4. Симплекс-метод в задачах лп

Симплексный метод позволяет, отправляясь от известного опорного решения задачи, за конечное число шагов получить оптимальное решение. Каждый из шагов состоит в нахождении нового решения, которому соответствует меньшее значение целевой функции, чем значение этой функции при предыдущем решении. Процесс повторяется до тех пор, пока не будет получен оптимальный план.

4.1. Основные положения симплекс-метода

Пусть задана задача линейного программирования в виде канонической модели.

(4.1)

Рассмотрим идею симплекс-метода на этом примере. Нетрудно убедиться, что система (4.1) совместна. Ее ранг r = 3, значит базисных переменных 3, а свободных переменных k = 5 – 3 = 2. Полагая свободные переменные x₄, x₅ равными нулю, получим первое опорное решение:

В начальном плане свободными, а значит равными нулю являются переменные х₄, х₅. Посмотрим, нельзя ли за счет увеличения х₄ и х₅ уменьшить значение целевой функции. У нас f(X) = 3  х₄+ х₅ , неизвестная х₅ входит в выражение целевой функции со знаком плюс, поэтому ее увеличение приводит к увеличению функции. И это нам невыгодно. В то же время неизвестная х₄ входит в выражениях со знаком минус. Поэтому ее увеличение сопровождается уменьшением значения функции f(Х). Увеличение свободной неизвестной х₄ вызывает соответствующие изменения базисных переменных х₁, х₂, х₃. Эти изменения могут оказаться такими, что базисные переменные станут отрицательными. Мы должны позаботиться о том, чтобы этого не произошло.

Оставим у переменной х₅  значение равное нулю и рассмотрим уравнения, которые в этом случае получаются из системы (4.1):

x₁ + x₄ = 2,

x₂ + 2x₄ = 7,

x₃ – x₄ = 2.

Так как х₁ = 2 – х₄ и , то х₄ < 2; аналогично х₂ = 7 – 2х₄ и , следовательно . Так как х₃ = 2 + х₄, то здесь х₄ может возрастать неограниченно. Далее выберем максимально возможное значение х₄ равное 2; при этом х₁ = 0, х₂ = 3, х₃ = 4, х₄ = 2, х₅ = 0.

Мы перешли к новому опорному решению: X_опор2 = (0, 3, 4, 2, 0). Сравнивая X_опор1 и X_опор2, видим, что х₁ стала свободной, а х₄  базисной. Модель надо преобразовать так, чтобы х₄ присутствовало только в первом уравнении системы (4.1), функция f(X) должна быть выражена через свободные переменные х₁ и х₅. Из первого уравнения х₄ = 2 – х₁ – х₅, и задача ЛП будет такой:

x ₂ – 2x₁ + x₅ = 3,

x ₃ + x₁ + 2x₅ = 4, (4.2)

x₄ + x₁ + x₅ = 2;

Теперь видно, что f(X) не может быть уменьшена за счет увеличения х₁ и х₅. Значит, мы получили оптимальное решение. Запишем его.

Х_min = (0, 3, 4, 2, 0); f_min= f(Х_min) = 1.

Идею, рассмотренную в примере, используем для того, чтобы сформулировать правило преобразования симплекс-таблиц для решения задач симплексным методом.