5.3. Примеры решения задач

Пример 1. Пусть дана задача линейного программирования:

5 х₁ + 5х₂ – x₃ = 5,

10х₂  х₄ = 5,

х ₁ + х₂ + x₅ = 5.

f(x) = 5x₂→ max.

Первое и второе уравнения не имеют базисных переменных, в третьем уравнении такой переменной является х_5. Чтобы получить каноническую модель задачи, вводим две базисные переменные:

5 х₁ + 5х₂ – x₃ +  ₁ = 5,

1 0х₂  х₄ +  ₂ = 5,

х₁ + х₂ + x₅ = 5,

где

, или .

Используя систему уравнений с базисными переменными и функцию цели , составляем исходную симплекс-таблицу.

Таблица 5.1

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
ξ1	5	5	5	-1	0	0	1	0
ξ2	5	0	10	0	-1	0	0	1
х5	5	1	1	0	0	1	0	0
φ()	10	5	15	-1	-1	0	0	0

Будем вводить в базис переменную х₁ и выводить ξ₁. Преобразуем первую строку так, чтобы в клетке разрешающего элемента была единица. Для этого разделим все элементы первой строки на 5. Получим новую первую строку для следующей таблицы (табл. 5.2).

Далее необходимо получить в столбце под переменной x₁ нули. Перепишем вторую строку без изменений, так как в ней на нужном месте уже стоит нуль. Остальные нули в столбце получим, умножив получившуюся первую строку на (1) и (5) и сложив ее поэлементно с третьей и четвертой строкой таблицы 5.1. Получаем новую симплекс-таблицу 5.2.

Таблица 5.2

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
х1	1	1	1	-1/5	0	0	1/5	0
ξ2	5	0	10	0	-1	0	0	1
х5	4	0	0	1/5	0	1	-1/5	0
φ()	5	0	10	0	-1	0	-1	0

Аналогично вводим в базис переменную х₂ вместо ξ₂. Для этого делим вторую строку таблицы 5.2 на 10, и результат записываем во вторую строку следующей таблицы (табл.5.3). Затем умножаем получившуюся вторую разрешающую строку на (1) и (10) и складываем ее поэлементно с первой и четвертой строкой таблицы 5.2. Новая симплекс-таблица имеет вид:

Таблица 5.3

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
х1	1/2	1	0	-1/5	1/10	0	1/5	-1/10
х2	1/2	0	1	0	-1/10	0	0	1/10
х5	4	0	0	1/5	0	1	-1/5	0
φ()	0	0	0	0	0	0	-1	-1

По теореме 1 метода искусственного базиса данная система имеет оптимальный план ( ), следовательно, по теореме 2 существует равносильная каноническая система, полученная из завершающей таблицы вспомогательной задачи.

Так как в завершающей симплекс-таблице вспомогательной задачи все вспомогательные переменные вышли из базиса, тогда, полагая их равными 0, получаем каноническую задачу для исходной задачи ЛП:

или

Составляем симплекс-таблицу по полученным данным:

Таблица 5.4

Базис	В	х1	х2	х3	х4	х5
х1	1/2	1	0	-1/5	1/10	0
х2	1/2	0	1	0	-1/10	0
х5	4	0	0	1/5	0	1
f1(x)	-5/2	0	0	0	1/2	0

Вводим в базис x₄. Выполняя обычные преобразования симплекс-метода и результаты вычислений запишем в табл.5.5.

Таблица 5.5

Базис	В	х1	х2	х3	х4	х5
х4	5	10	0	-2	1	0
х2	1	1	1	-1/5	0	0
х5	4	0	0	1/5	0	1
f1(x)	-5	-5	0	1	0	0

Вводим в базис х₃ . Получаем следующую таблицу 5.6.

Таблица 5.6

Базис	В	х1	х2	х3	х4	х5
х4	45	10	0	0	1	10
х2	5	1	1	0	0	1
х3	20	0	0	1	0	5
f(x)	-25	-5	0	0	0	-5

Так как в индексной строке нет положительных элементов, следовательно, получили завершающую симплекс-таблицу, в которой содержится оптимальный план задачи.

Х_опт = (0, 5, 20, 45, 0)

f_min(x) = 25 , тогда f_max(x) = 25.

Пример 2. Дана основная задача линейного программирования. При помощи элементарных преобразований матрицы коэффициентов системы ограничений, привести задачу к стандартному виду и решить ее геометрическим методом. Методом искусственного базиса получить каноническую задачу (или доказать несовместность этой системы). Решить полученную модель с помощью симплекс- таблиц (или доказать, что она не имеет оптимального плана).

Запишем и преобразуем матрицу коэффициентов системы.

→ →

Получили систему ограничений с единичным базисом (х₃; х₄; х₅):

Отбрасывая базисные переменные, получим стандартную задачу ЛП:

Выразим функцию цели через свободные неизвестные х₁ и х₂. Имеем:

тогда

Решим задачу геометрическим способом, как показано в разделе 2. Область планов представляет собой треугольник АВС и функция цели достигает максимального и минимального значения в его вершинах:

Из рисунка видно, что точка В(3, 4) − точка максимума, тогда:

f(X_опт) = 3 + 2·4 = 11.

Для решения задачи симплекс-методом приведем систему ограничений к каноническому виду методом искусственного базиса. Заменив знаки в третьем ограничении, сделаем правые части уравнений неотрицательными:

Очевидно, что в третьем уравнении нет базисной переменной. Используем метод искусственного базиса. Введем в это уравнение вспомогательную переменную ξ. Теперь решим вспомогательную задачу по минимизации функции симплекс-методом.

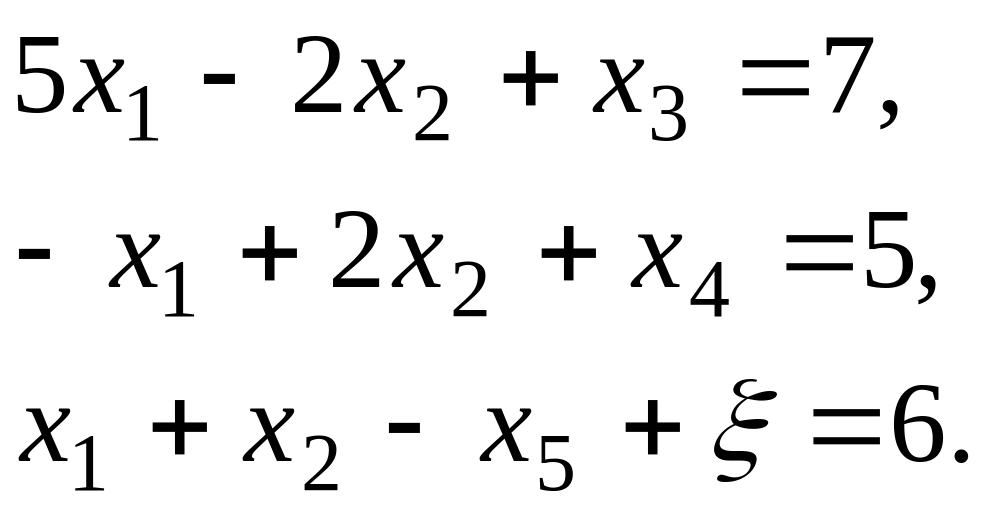
Занесем эту задачу в таблицу

Таблица 1

Б	В	х1	х2	х3	х4	х5	ξ
x3	7	5	-2	1	0	0	0
x4	5	-1	2	0	1	0	0
ξ	6	1	1	0	0	-1	1
	6	1	1	0	0	0	0

Введем в базис х₂, тогда из базиса выйдет переменная х₄. Пересчитывая таблицу, получим:

Таблица2

Б	В	х1	х2	х3	х4	х5	ξ
x3	12	4	0	1	1	0	0
x2	2.5	-0.5	1	0	0.5	0	0
ξ	3.5	1.5	0	0	-0.5	-1	1
	3.5	1.5	0	0	-0.5	-1	0

Введем в базис х₁, тогда из базиса выйдет переменная ξ. Пересчитывая таблицу, получим:

Таблица 3

Б	В	х1	х2	х3	х4	х5	ξ
x3	8/3	0	0	1	7/3	8/3	-8/3
x2	11/3	0	1	0	1/3	-1/3	1/3
x1	7/3	1	0	0	-1/3	-2/3	2/3
	0	0	0	0	0	0	-1

Данная таблица - завершающая таблица метода, она содержит оптимальный план вспомогательной задачи. Поскольку, , то, отбрасывая последний столбец, получаем каноническую систему для исходной задачи.

Выразим функцию цели через свободные переменные:

и решим исходную задачу симплекс-методом.

Б	В	х1	х2	х3	х4	х5
x3	8/3	0	0	1	7/3	8/3
x2	11/3	0	1	0	1/3	-1/3
x1	7/3	1	0	0	-1/3	-2/3
f1(X)	-29/3	0	0	0	-1/3	4/3

Выполняя преобразования, получаем оптимальный план, доставляющий минимум функции цели f₁(X) .

Б	В	х1	х2	х3	х4	х5
x5	1	0	0	0.375	0.875	1
x2	4	0	1	0.25	0.25	0
x1	3	1	0	0.125	0.625	0
f1(X)	-11	0	0	-0.5	-1.5	0

Получен оптимальный план. Запишем ответ

Х_опт = (3; 4; 0; 0;1);

f₁(X_опт) = 11 (min), тогда f₁(X_опт) = 11 (max).