7.3. Решение задачи о назначениях венгерским методом

Теорема Кенига. Если к стоимостям какой-либо строки (столбца) задачи о назначениях прибавить одно и тоже число, то оптимальный план не изменится.

Алгоритм решения, основанный на этой теореме:

1) выбрать в каждой строке минимальный элемент и вычесть его из всех элементов этой строки;

2) если в каком-нибудь столбце не появилось нулей, то из всех элементов такого столбца вычитается минимальный элемент этого столбца;

3) рассматривается множество нулей таблицы и, если оно допустимо, то задача решена, иначе переходим к пункту 4;

4) минимальным числом прямых по строкам и столбцам вычеркиваются все нули, а из невычеркнутых элементов выбирается минимальный элемент ;

5) величина вычитается из невычеркнутых и прибавляется к дважды вычеркнутым элементам, после чего переходим к пункту 3.

Замечание. Допустимое множество нулей определяется следующим образом. Нулевой элемент в таблице с номером ij означает возможность выполнения i-тым исполнителем всей работы j. Поэтому расположение нужного количества нулей в таблице должно позволить выбрать единственным способом распределение всех работ между всеми исполнителями.

Сформулируем правило нахождения оптимального решения задачи о назначениях, в которой целевая функция минимизируется. Рассмотрим решение задачи на примере. Пусть задана матрица стоимости выполнения работ, причем для пяти работ имеется пять исполнителей.

1. Выберем в каждой строке матрицы наименьший элемент и вычтем его из каждого элемента этой строки.

2. Выберем столбцы, в которых нет нулей и найдем в них наименьший элемент. Затем вычтем его из каждого элемента столбца.

.

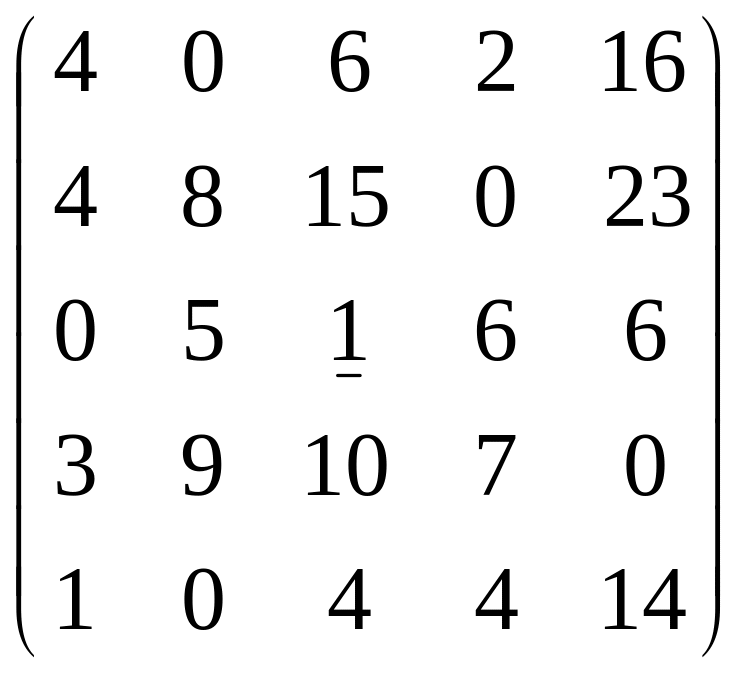
3. Попробуем составить опорное решение из нулей, входящих в полученную матрицу. Но допустимого множества нулей не получено. В частности, выбрав один из нулей во втором столбце, например верхний (работа А₁ распределена второму исполнителю), мы не сможем использовать нижнюю строку с оставшимся нулем. Это означает, что работа А₅ останется нераспределенной.

4. В ычеркиваем все нули, проведя наименьшее число прямых, проходящих через все нули в матрице. Среди незачеркнутых найдем наименьший элемент, это элемент (он дважды подчеркнут в получившейся матрице), вычитаем его из всех невычеркнутых и прибавляем ко всем дважды вычеркнутым.

5. Снова пытаемся составить опорное решение. Допустимое множество нулей получено (выделено двойным подчеркиванием). Из таблицы следует, что первый исполнитель выполняет работу 5, второй – работу 1 и т.д. Запишем решение в виде матрицы

Возвращаясь к исходной матрице, вычисляем минимальное значение функции цели:

.

7.4. Решение задачи максимизации

Известно, что переход от задачи минимизации к задаче максимизации в линейном программировании достигается изменением знака функции цели.

, следовательно, данную задачу на нахождение max можно превратить в задачу минимизации, заменив знаки всех элементов в матрице стоимостей. Далее решение находится методом, рассмотренным выше. Пусть известен доход, который можно получить при назначении каждого исполнителя i (i = 1, 2,…, n) на любую работу j (j = 1, 2,…, n). Найдем распределение исполнителей, которое принесет максимальную прибыль.

Дана матрица

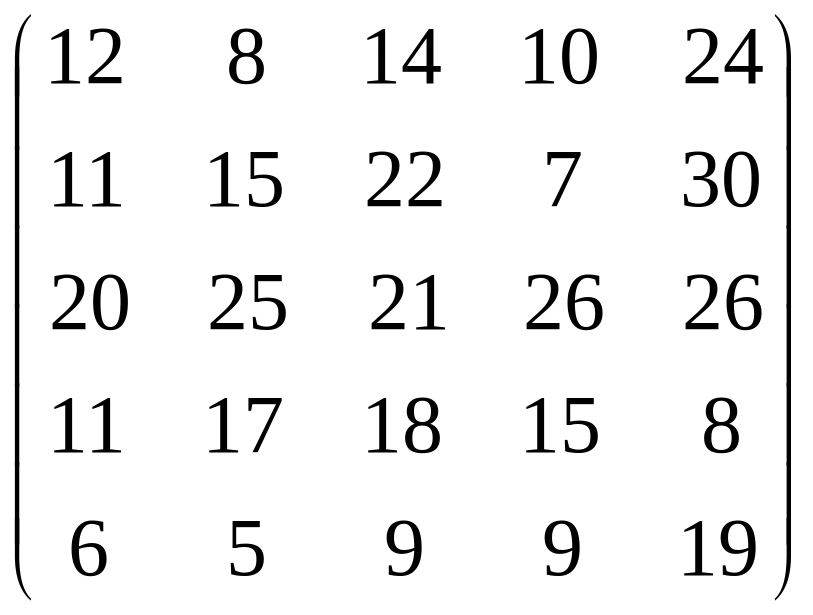, меняя знаки, имеем:

Прибавим к элементам всех строк модуль максимального элемента в таблице (он равен 26), а затем проделаем шаги 1 и 2.

.

М ножества допустимых нулей в матрице нет, следовательно, продолжаем решение.

Получили оптимальное решение. Вычислим максимум функции цели, наложив эти нули на исходную матрицу.

,

при этом первый исполнитель выполняет первую работу, второй – четвертую, третий  вторую и т.д.