2.3.Элементы симметрии.

Элементами симметрии являются:

•плоскость симметрии,

•ось симметрии,

•центр симметрии

•зеркально-поворотная ось симметрии.

Любую симметрию кристалла удобно представить как совокупность отдельных элементов симметрии, каждому из которых соответствует какая-

нибудь из упомянутых операций.

Ось симметрии (рис. 2.3.1). Если кристалл обладает осью симметрии (поворотной осью), то он может быть совмещен сам с собой, т.е. приведен в положение неотличимое от исходного, путем поворота на некоторый угол вокруг этой оси. В зависимости от симметрии кристалла величина угла поворота, необходимого для совмещения кристалла с самим собой, может составлять 360, 180, 120, 90, 60 градусов. (2π / п, где n = 1, 2, 3, 4 или 6). В соответствии с этим ось симметрии называют осью первого, второго, третьего, четвертого или шестого порядка. Других осей симметрии не существует. Это связано с тем, что по определению при повороте кристалл должен совместиться сам с собой, т.е. пространство должно быть заполнено без промежутков. А из геометрии известно, что плоскость можно заполнить лишь треугольниками, параллелограммами и шестиугольниками, а пространст-во – телами, грани которых представлены этими фигурами.

П лоскость симметрии (рис. 2.3.2). Если одна половина кристалла совмещается с другой при отражении в некоторой плоскости, как в зеркале, то такая плоскость называется плоскостью симметрии. Например, для прямоугольника, плоскостями симметрии являются плоскости 1-1 и 2-2. Части фигуры по обе стороны этих плоскостей являются зеркальным отражением друг друга. Но плоскость 3-3, также делящая фигуру пополам, не является плоскостью симметрии, так как отражение в ней одной половины не совпадает с изображением другой.

Ц ентр симметрии. Если в кристалле существует точка, обладающая тем свойством, что при замене радиуса – вектора , любой из частиц, составляющих кристалл на обратный ему вектор , кристалл переходит в состояние, неотличимое от исходного, то эта точка называется центром симметрии или центром инверсии.

Поворотно-зеркальная ось (рис. 2.3.3). К этому элементу симметрии приводит одновременное применение двух операций: поворота вокруг оси и зеркального отражения в плоскости, перпендикулярной оси. Это значит, что кристалл обладает поворотно-зеркальной осью симметрии, если его можно совместить с самим собой, повернув на некоторый угол вокруг оси и отразив затем в плоскости, перпендикулярной к этой оси. Если угол поворота, равен 2π /n , то п определяет порядок поворотно-зеркальной оси.

Симметрия любого кристалла может быть описана с помощью перечисленных четырех элементов симметрии. Причем перечисленные элементы симметрии могут в кристаллах по-разному комбинироваться.

Характерной особенностью кристалла является периодичность его внутренней структуры. Идеальный кристалл можно получить путем регуляр-ного повторения примитивной ячейки в трех направлениях без изменения ориентации. Можно говорить об инвариантности идеального бесконечного кристалла относительно трансляций вида:

(2.3.1)

Параллелепипед, построенный на трех некомпланарных векторах образует примитивную ячейку кристалла.

Кроме трансляционной симметрии кристалл обладает и вращательной симметрией. Для обозначения операций симметрии, связанных с поворотами вокруг оси, вводится своя символика. Так, поворот на угол 2π / n вокруг оси обозначается символом С_n, где n - порядок оси. Отражение в плоскости обо-значается символом σ, к которому добавляется нижний индекс, указывающий направление нормали к плоскости (индексом h обозначают горизонтальную плоскость, а индексом v - вертикальную). Инверсия обозначается символом J. Для описания составных операций можно пользоваться операторной симво-ликой. Так, запись BA означает, что выполняется операция A, а затем опера-ция B. Результат обозначается буквой C : C=BA.

Две операции равны, если их результат идентичен. Зеркальный поворот обозначают символом S_n. Для этой операции получаем по определению:

(2.3.2)

Между операциями разных видов существуют определенные соотно-шения эквивалентности. Например, результатом последовательных отраже-ний в двух плоскостях, образующих между собой угол , θ = π/n будет поворот на угол 2π/n вокруг линии их пересечения.

П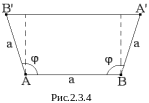 ериодичность кристалла накладывает ограничения на порядок n осей поворотов и зеркальных поворотов. А именно, в кристалле могут существо-вать только оси второго, третьего, четвертого и шестого порядков. Это видно из рис. 2.3.4.

Пусть a – наименьший период кристалла в направлении AB. Пусть через точку A проходит (перпендикулярно плоскости рисунка) ось симмет-рии. Точка B является трансляционно эквивалентной и через нее проходит другая такая же ось симметрии.

Произведем поворот вокруг оси, проходящей через A на угол φ = 2π/n. Тогда точка B перейдет в точку B'. Аналогично поворот вокруг B переводит точку A в A'. Если повороты являются операциями симметрии кристалла, то точки A' и B' должны быть трансляционно эквивалентными и расстояние A'B' должно быть равно ap с целым p. Это приводит к уравнению

a + 2asin(φ-π/2) = a - 2acosφ = ap (2.3.3)

или

cosφ = (1 - p) / 2 (2.3.4)

Так как , то p=3, 2, 1, 0, а n=2, 3, 4, 6.

Кроме чистых поворотов и чистых трансляций кристаллическая решетка может обладать еще и особыми элементами симметрии, представ-ляющими собой комбинации параллельных переносов с поворотами и отражениями. Например, комбинация поворота с трансляцией приводит к появлению винтовой оси. Решетка обладает винтовой осью n-ого порядка, если она совмещается сама с собой при повороте вокруг оси на угол 2π/n и одновременной трансляции на расстояние d вдоль этой оси. Причем d = pa/n (p = 1, 2...n-1), где a – наименьший период решетки вдоль этой оси. Кроме того, комбинация отражения в плоскости с трансляцией на полпериода решетки вдоль направления, лежащим в плоскости отражения, называется плоскостью скольжения.

Пространственные элементы симметрии за исключением операций трансляции – это винтовые оси и плоскости скольжения.

Говорят, что кристалл обладает винтовой осью n-го порядка, если при повороте на угол 360· /n относительно этой оси и смещении на вектор р, параллельный оси и не равный ни одному из векторов трансляции, кристалл переходит в состояние, тождественное исходному. Ось называют винтовой, так как при движении по винтовой резьбе поворот также сопровождается смещением вдоль оси винтовой резьбы.

Говорят, что кристалл обладает плоскостью скольжения, если при зеркальном отражении относительно этой плоскости и последующем пере-мещении на вектор br, параллельный плоскости отражения и не равный ни одному из векторов трансляции, кристалл переходит в состояние, тождественное первоначальному.

Все вышеописанные операции принадлежат к точечным элементам симметрии. При повороте относительно некоторой оси на месте остаются точки кристалла, лежащие на оси симметрии, при отражении – точки, лежащие на плоскости симметрии, а при инверсии остается на месте точка, совпадающая с центром инверсии.

При анализе ряда явлений, которые можно назвать макроскопически-ми, кристалл ведет себя как однородное сплошное тело. В этом случае свойства кристалла зависят только от направления в нем. Сложная структура примитивной ячейки не важна при анализе оптических, тепловых и упругих свойств кристаллов.

Трансляционная симметрия решетки не приводит к эквивалентности каких-либо направлений. Поэтому симметрия направлений, а следовательно и макроскопических свойств кристалла, определяется совокупностью его осей и плоскостей симметрии, причем винтовые оси и плоскости скольжения надо рассматривать как простые оси и плоскости. Такие совокупности элементов называются кристаллическими классами.