Математический анализ определенный интеграл, несобственный интеграл, приложения определенного интеграла

Замечания.

1.

Если

(AB задана явным уравнением

y = f ( x) , x [a, b],

a < b ,

и если

f ′( x) C [a, b] ,

то

для

любого

x [a, b]:

l′( x) =

1 +

[

f ′( x) 2

и

(

)

]

dl = 1 +

[

f ′( x)

2 dx .

]

2. Если (AB

задана

уравнением

в

полярных координатах

r = r (ϕ) ,

ϕ [α,β],

α <β,

и

если

r′

C [α,β]

,

то

для

любого

ϕ [α,β]:

ϕ

(

)

l′(ϕ) =

[

r (ϕ) 2

+

[

r′(ϕ)

2 и dl =

[

r (ϕ)

2

+

[

r′(ϕ) 2 dϕ.

]

]

]

]

§3. Площадь поверхности вращения

Понятие площади кривой поверхности в общем случае будет дано позднее

(при рассмотрении приложений двойного интеграла). Здесь же мы остановимся

лишь на случае поверхности вращения.

Пусть в плоскости Oxy дана спрямляемая дуга (AB . Станем вращать эту

дугу вокруг оси Ox. Мы получим при этом поверхность вращения, о площади S

которой и пойдет речь.

Возьмем

на

(AB ряд точек, следующих

y

M n−1

B =Mn

друг

за

другом

вдоль

кривой:

A = M0 ,

M1, K,

Mn = B. Соединяя последова-

M 2

тельно эти точки прямолинейными отрезками,

M0 =A M1

получим ломаную

M0 M1KMn ,

вписанную в

x

(AB . При вращении этой ломаной также по-

лучится некоторая поверхность вращения. Она

будет состоять из боковых поверхностей усе-

ченных конусов и, быть может, из боковых по-

верхностей конусов и цилиндров. Обозначим

через Sлом. площадь поверхности, образован-

Рис. 3.21. К определению

ной вращением

ломаной

M0 M1KMn

вокруг

оси Ox (рис. 3.21).

площади поверхности вращения

Отметим, что для закрепленного числа n и

закрепленного

способа

выбора точек M1, M2 , K, Mn−1

значение

величины

Sлом.

будет

вполне

определенным

числом.

Если

же

число

точек

M0 , M1, K, Mn

и способы их выбора на (AB менять, то будет изменяться,

вообще говоря, значение величины Sлом. .

Определение. Если существует конечный предел

S = lim Sлом. ,

(1)

λ→0

121

не зависящий от способа вписывания ломаной, то этот предел принимают за площадь поверхности, получаемой при вращении (AB вокруг оси Ox (здесь

λ =	max		Mk Mk +1		).
k =0, n−1
Теорема 1. Пусть (AB задана параметрическими уравнениями
					x = x (t),	t [α,β], α <β.
					y = y (t),
(Считаем			(AB незамкнутой и не имеющей кратных точек.) Пусть функции
x (t), y (t)			имеют в [α,β] непрерывные производные x′(t) , y′(t) . Тогда поверх-

ность, образованная вращением (AB вокруг оси Ox, имеет площадь S, причем

			β
			S = 2π∫ y(t) (xt′)2 +( yt′)2 dt .				(2)
			α
*	Пусть для определенности (AB			лежит выше оси Ox, т.е.			y(t) ≥ 0,
t [α,β]. Впишем в (AB ломаную M0 M1KMn ( M0 = A , Mn = B ),							причем
сделаем это так: разделим промежуток				[α,β] точками α = t0 < t1 <K< tn = β
произвольным образом на части [tk , tk+1],				k =		, и возьмем в качестве то-
					0, n −1
чек Mk ,	k =		, точки (xk , yk ) , у которых xk = x (tk ), yk = y (tk ) . Рассмот-
		0, n −1

рим k-е звено ломаной. Может реализоваться один из следующих трех случаев

(рис. 3.22, 3.23, 3.24).

a)

y

M

k +1

b)

y

M

k +1

c)

y M k

M

k +1

M k

x

M k

x

x

xk

xk +1

xk

xk +1

xk

xk +1

Рис. 3.22

Рис. 3.23

Рис. 3.24

Различные случаи положения звена ломаной относительно оси вращения

Площадь поверхности, образованной вращением звена

Mk Mk+1

вокруг оси

Ox, будет равна

yk + yk +1

S

k

= 2π

M

k

M

k +1

.

(3)

2

Заметим, что выражение (3) остается одним и тем же, независимо от того, какой из трех случаев a), b), или с) реализуется. Имеем

Mk Mk +1 = (xk+1 − xk )2 +( yk+1 − yk )2 = [x (tk+1 ) − x (tk )]2 +[y (tk +1 ) − y (tk )]2 .

122

Замечаем, что функции x (t), y (t) в промежутке [tk , tk +1] удовлетворяют усло-

виям теоремы Лагранжа. Следовательно, можно написать

x (tk +1 ) − x (tk ) = x′(τk ) ∆tk , τk [tk , tk+1], y (tk +1 ) − y (tk ) = y′(θk ) ∆tk , θk [tk , tk +1].

Тогда
		Mk Mk +1		=		[x′(τk )]2 +[y′(θk )]2 ∆tk ,
Sk = 2π	y (tk ) + y (tk +1 )					[x′(τk )]2 +[y′(θk )]2 ∆tk , k =		.
							0, n −1
2
Для площади Sлом. , образованной вращением всей ломаной M0 M1KMn									вокруг
оси Ox, будем иметь
	n−1
Sлом. = π∑[y (tk ) + y (tk +1 )] [x′(τk )]2 +[y′(θk )]2 ∆tk .									(4)
	k =0
Введем в рассмотрение сумму
		n−1
	σ = 2π∑y (τk ) [x′(τk )]2 +[y′(τk )]2 ∆tk .								(5)

k =0

Видим, что σ является интегральной суммой Римана для интеграла

β

J = 2π∫y (t) [xt′(t)]2 +[yt′(t)]2 dt .

α

Из условий теоремы следует, что подынтегральная функция в J есть функция непрерывная на промежутке [α,β], следовательно, интеграл J существует. Зна-

чит,		lim σ существует и равен
	~
~		λ→0
		max	{∆tk }. Заметим, что λ → 0
λ =
	k =0, n−1

β	[xt′(t)]2 +[yt′(t)]2 dt . (Здесь
2π∫y (t)

α

~

λ → 0 .)

Рассмотрим очевидное равенство

Sлом. = σ +(Sлом. −σ).			(6)
Из (6) видим, что теорема будет доказана, если показать, что
lim (S	лом.	−σ) = 0.	(7)
~
λ→0

Имеем

n−1

Sлом. −σ = π∑[y (tk ) + y (tk +1 )] [x′(τk )]2 +[y′(θk )]2 ∆tk −

k =0

n−1

−π∑2 y (τk ) [x′(τk )]2 +[y′(τk )]2 ∆tk =

k =0

123

	n−1
= π∑[y (tk ) + y (tk +1 ) −2 y (τk )]			[x′(τk )]2 +[y′(θk )]2 ∆tk +
n−1	k =0
	2 y (τk )	[x′(τk )]2 +[y′(θk )]2	− [x′(τk )]2 +[y′(τk )]2
+π∑				∆tk .	(8)
k =0

Произведем оценку обеих сумм, стоящих в правой части (8). Возьмем ε > 0

– любое.

t

t

(

)

t

t

1. По условию, x′(t), y′(t) C

[α,β]

x′(t), y′(t) – ограниченные в [α,β]

существует L > 0

такое,

что

xt′(t)

≤ L ,

yt′(t)

≤ L , для любого t [α,β]

[xt′(t)]2 +[yt′(t)]2 ≤ L 2 , t [α,β],

[xt′(τk )]2 +[yt′(θk )]2 ≤ L 2 , k =

.

0, n −1

Тогда будем иметь

n−1

π∑[y (tk ) + y (tk +1 ) −2 y (τk )]

[xt′(τk )]2 +[yt′(θk )]2 ∆tk

≤

k =0

n−1

≤ πL

2 ∑(y (tk +1 ) − y (τk ) + y (tk ) − y (τk ) ) ∆tk .

(9)

По условию

(

k =0

)

y (t) –

равномерно непрерывная на [α,β]

y (t) C [α,β]

взятому ε > 0

отвечает δ1 > 0 , зависящее только от ε, такое, что для любых двух

точек t′, t′′ из [α,β], для которых

t′′ −t′

< δ1 , будет

y (t′′) − y (t′) < 4

ε

(10)

2 πL(β−α) .

Если брать дробление промежутка [α,β] на части [tk , tk +1] любое, но такое, что

~

~

,

то будем иметь сразу

для всех k = 0, n −1:

tk − τk

,

λ < δ1

≤ λ < δ1

tk +1 − τk

~

≤ λ < δ1 , откуда, принимая во внимание (10), получим:

y (tk ) − y (τk ) <

ε

; y (tk +1 ) − y (τk ) <

ε

.

πL(β−α)

πL(β−α)

4 2

4 2

А значит, из (9)

n−1

2

2

ε

π∑[y (tk ) + y (tk +1 ) −2 y (τk )] [xt′(τk )]

+[yt′(θk )] ∆tk

<

2 .

k =0

(

)

y (t) – ограниченная на [α,β]

2. По условию y (t) C [α,β]

~

> 0

такое, что

y (t)

≤

~

[α,β]

y (τk )

~

вует L

L , t

≤ L , k = 0, n −1.

Имеем

n

−1

2 y (τk )

[x′(τk )]2 +

[y′(θk )]2 −

[x′(τk )]2 +[y′(τk )]2

π∑

∆tk

k =0

(11)

сущест-

≤

124

≤

~ n−1

2

2

2πL

∑

[yt′(θk )]

−[yt′(τk )] ∆tk

k =0

(здесь использовано неравенство:

N −

M

≤

N − M

, где N и M – любые две

неотрицательные величины).

[

t

]

(

)

t

(

)

По условию y′(t) C [α,β]

y′(t) 2

C [α,β]

по теореме Кантора:

взятому

ε > 0

отвечает

δ2 > 0 ,

зависящее только от ε, такое, что для любых

двух

точек

t′, t′′ [α,β],

для

которых

t′′ −t′

< δ2 ,

будет

[yt′(t′′)]2 −[yt′(t′)]2

<

~

2

ε2

2

.

(2πL )

4(β−α)

Возьмем дробление промежутка [α,β] на части [tk , tk +1] любое, но такое,

~

θk − τk

~

и, следователь-

чтобы было λ < δ2 . Тогда для всех k = 0, n −1:

≤ λ < δ2

но, сразу для всех k =

:

[yt′(θk )]2 −[yt′(τk )]2

<

ε2

2

. Тогда

0, n −1

~

2

будем иметь

(2πL )

4(β−

α)

n−1

~

~

2

2

ε (β−α)

ε

∑

<

2πL

=

.

(12)

2πL

[yt′(θk )]

−[yt′(τk )] ∆tk

~

(β−α)

2

k =0

2πL 2

Положим δ = min{δ1,δ2} и возьмем дробление промежутка [α,β] на части

~

[tk , tk +1] любое, но такое, чтобы было λ < δ. Тогда будут выполняться одновре-

менно оба неравенства (11) и (12) и, следовательно,

Sлом. −σ

< ε.

~

Последнее неравенство получено нами лишь в предположении,

что λ < δ. Зна-

чит, lim (S

лом.

−σ) = 0.

~

λ→0

Частные случаи.

1°. Теорема 2. Пусть (AB кривой задана явным уравнением

y = y (x), x [a, b],

a < b.

Пусть функция

y ( x)

имеет в промежутке [a, b]

непрерывную производную

y′(x) . Тогда поверхность, образованная вращением (AB вокруг оси Ox, имеет площадь S, причем

b
S = 2π∫ y ( x) 1+( yx′ )2 dx .	(13)

a

Представление (AB кривой явным уравнением y = y (x) , x [a, b], может быть рассмотрено как параметрическое:

125

x = t,	t [a, b], a < b .
y = y (t),

Тогда утверждения, высказанные в этой теореме, сразу вытекают из предыдущей теоремы.

2°. Теорема 3. Пусть (AB кривой задана уравнением в полярных координатах

r = r (ϕ), ϕ [α,β], α <β.

Пусть функция r (ϕ) имеет в [α,β] непрерывную производную r′(ϕ). Тогда по-

верхность, образованная вращением (AB вокруг полярной оси (вокруг оси Ox), имеет площадь S, причем

β
S = 2π∫r (ϕ) sin ϕ [r (ϕ)]2 +[r′(ϕ)]2 dϕ.	(14)

α

Утверждения, высказанные в теореме 3, вытекают из теоремы 1, если принять ϕ за параметр и вспомнить, что x = r cos ϕ, y = r sin ϕ.

3°. Формулы (2), (13), (14) для площади S поверхности вращения могут быть объединены в одну, а именно

( B)
S = 2π ∫ρdl .	(15)

( A)

Здесь ρ есть расстояние от точек (AB ренциал длины дуги кривой. Символы

кривой до оси вращения; dl – диффе- ( A) и (B) показывают, что нужно ин-

тегрировать между теми пределами для независимой переменной, которые соответствуют данным точкам кривой A и B.

y B a

−a	A x
	a

−a

Рис. 3.25. К вычислению площади поверхности вращения в примере 1

		3	t,
x = a cos				вращает-
Пример 1. Астроида	3
			t
y = a sin

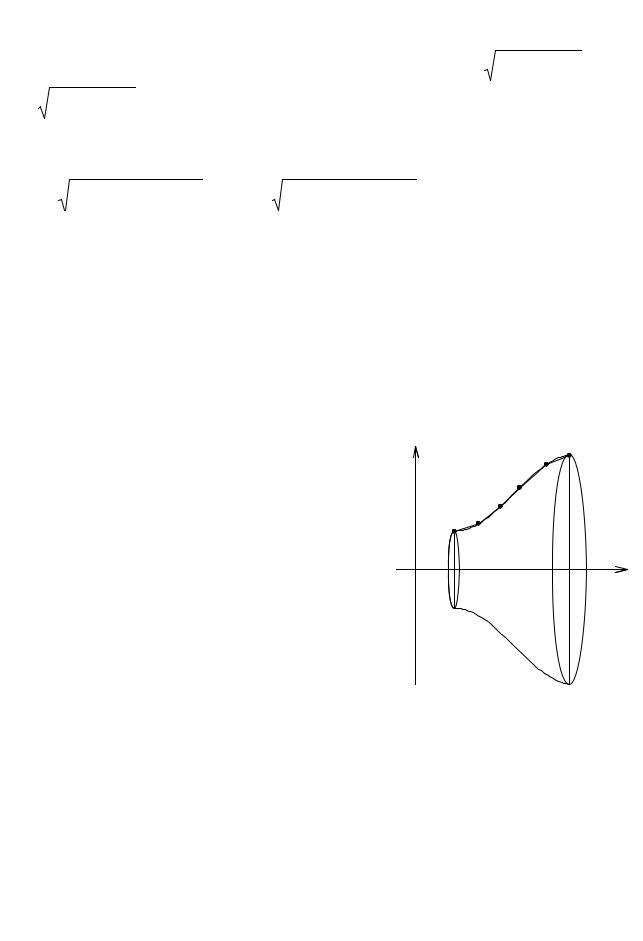
ся вокруг оси Ox. Найти площадь S поверхности вращения (рис. 3.25).

Воспользовавшись симметрией фигуры,

~

достаточно вычислить площадь S поверхности, образованной вращением (AB астроиды вокруг оси Ox.

(AB представляется параметрическими

уравнениями
		3	t,			π
x = a cos				t
	3				0,	2	.
			t,
y = a sin

Тогда:

126

ρ =

y (t)

a sin3 t

= a sin3 t ,

так как sin t ≥ 0 , если t

π

;

0,

2

dl =

( x′)2

+( y′)2 dt =

9a2 sin2 t cos2 t dt = 3a sin t cos t dt ,

t

t

так как sin t ≥ 0 , cos t ≥ 0 , если t

π

0,

2

.

Имеем

π 2

π 2

~

= 2π ∫a sin3 t 3a sin t cos t dt = 6πa2 ∫sin4 t cos t dt =

S

0

6

π 2

6

0

=

πa

2

sin

5

t

=

πa

2

(кв. ед.).

5

0

5

~

12

2

y

Так как S = 2S , то S =

5

πa

(кв. ед.).

B

y=x

= a cos

3

t,

a

Пример 2. Астроида

x

вращает-

3

= a sin

t

y

C

A

ся вокруг прямой

y = x . Найти площадь S по-

x

верхности вращения (рис. 3.26).

~

– площадь поверхности, обра-

−a

a

Пусть S

зованной вращением

(AB астроиды вокруг

прямой

y = x ,

а

~

площадь поверхности,

S –

образованной вращением (BC астроиды во-

−a

круг этой прямой. Тогда, приняв во внимание

Рис. 3.26. К вычислению площади

симметрию

фигуры,

будем

иметь

~

~

поверхности вращения в

S = 2(S

+ S ) .

примере 2

Имеем:

3

t,

π

π

(AB:

x = a cos

t

,

,

dl = 3a sin t cos t dt ,

3

4

2

t,

y = a sin

3

t,

π

3π

(BC:

x = a cos

t

,

,

dl = −3a sin t cos t dt .

3

2

4

t,

y = a sin

(

)

Найдем расстояние ρ от точек астроиды

y = x (до

x (t), y (t) до прямой

прямой y − x = 0 ). Имеем

ρ =

x (t) − y (t) =

1

a cos3 t −a sin3 t = a (sin3 t −cos3 t),

2

2

2

127

так как для t		π	,	π			π	,	3π		:	sin	3	t −cos	3	t ≥ 0. Следовательно,
		4		2	U		2		4

~

π 2

a2

π 2

= 2π ∫

(sin3 t

−cos3 t) 3a sin t cos t dt = 3

2πa2 ∫(sin4 t cos t −sin t cos4 t) dt =

S

π 4

π 4

=

3 2

πa

2

(sin

5

t +cos

5

t)

π 2

=

3 2

πa

2

1

5

5

1−

2

(кв. ед.),

3π 4

π 4

2

~

a2 (sin3 t −cos3 t) (−3a sin t cos t) dt =

= 2π ∫

S

π 2

3π 4

= 3 2πa2 ∫(sin t cos4 t −sin4 t cos t) dt =

π 2

= 3

5

2

πa2 (−sin5 t −cos5 t) 3π 4 = 3

2 πa2

(кв. ед.),

π 2

5

y

~

~

=

3

2

πa

2

2 −

1

S

+ S

5

2 2

(кв. ед.);

B (0,a)

~

~

3

2

(4 2

−1)(кв. ед.).

S =

2(S

+ S ) = 5 πa

= a cos

3

t,

x

ле-

Пример 3. Дуга астроиды

3

t,

y = a sin

A(a,0 )

жащая в первой четверти, вращается около сво-

x

ей хорды (рис. 3.27). Найти площадь S поверх-

ности вращения.

Рис. 3.27. К вычислению

Уравнение хорды, стягивающей (AB ас-

площади поверхности вращения

троиды,

будет

таким:

x

+

y

=1

в примере 3

x + y −a = 0.

a

a

= a cos

3

t,

π

(AB:

x

t

dl = 3a sin t cos t dt .

3

0,

,

= a sin

t,

2

y

(

)

Найдем расстояние ρ от точек астроиды

до прямой

x + y −a = 0.

x (t), y (t)

Имеем

ρ = x (t) + y (t) −a =

1

a cos3 t +a sin3 t −a

= a

(1−cos3 t −sin3 t),

2

2

π

2

так как 1−cos

3

t −sin

3

t ≥ 0

для t 0,

2

. Следовательно,

128

π 2

a2 (1−cos3 t −sin3 t) 3a sin t cos t dt =

S = 2π ∫

0

π 2

= 3

2 πa2 ∫(sin t cos t −cos4 t sin t −sin4 t cos t) dt =

0

π 2

= 3

2 πa

2

1

sin

2

t +

1

cos

5

t −

1

sin

5

3 2

πa

2

(кв. ед.).

2

5

5

t

=

10

0

Пример 4. Лемниската r = a

вращается

вокруг полярной

оси.

cos 2ϕ

Найти

площадь

S

поверхности

вращения (рис. 3.28).

Принимая во внимание симметрию фигуры, достаточно вычислить пло-

щадь

поверхности,

образованной

вращением (AB

лемнискаты

вокруг

оси

(AB

r = a

π

ϕ = 0 .

представляется

уравнением

cos 2ϕ

, ϕ 0,

. Здесь

π

4

ρ = y = r sin ϕ

ρ = a cos 2ϕ sin ϕ, ϕ

0,

4

.

dl =

r

2

(ϕ) +[r′

2

dϕ =

a

2

2ϕ

+a

2 sin2 2ϕ

dϕ

a dϕ

.

]

cos

=

ϕ

cos 2ϕ

cos 2ϕ

Поэтому

π 4

π 4

~

a dϕ

= 2π ∫ a

2

∫sin ϕdϕ =

S

cos 2ϕ sin ϕ

cos 2ϕ = 2πa

0

0

= −2πa

2

cos

ϕ

π 4

= 2πa

2

1

(кв. ед.).

0

1−

~

2

(2 −

2)(кв. ед.).

= 2πa2

Тогда S = 2S

y

y

B	A	x	B	A	x

Рис. 3.28. К вычислению площади		Рис. 3.29. К вычислению площади
поверхности в примере 4		поверхности вращения в примере 5
Пример 5. Лемниската r = a		вращается вокруг оси ϕ = π . Найти
	cos 2ϕ
		2

площадь S поверхности вращения (рис. 3.29).

129

И здесь, воспользовавшись симметрией фигуры, достаточно найти пло-

~

щадь S поверхности, образованной вращением (AB лемнискаты вокруг оси

ϕ =

π

(вокруг

оси Oy).

(AB

представляется уравнением

r = a

cos 2ϕ ,

2

π

π

ϕ

ρ = x

= r cos ϕ

ρ = a

cos 2ϕ cos ϕ

, ϕ

;

0,

. В этом случае

0,

4

4

a dϕ

dl =

.

cos 2ϕ

Поэтому

π 4

π 4

~

a dϕ

= 2π ∫ a

2

∫cos ϕdϕ =

S

cos 2ϕ cos ϕ

cos 2ϕ = 2πa

0

0

y

= 2πa2 sin ϕπ0

4 =

2 πa2 (кв. ед.).

y=x

Пример

6.

Лемниската

r = a

cos 2ϕ

вращается вокруг оси

ϕ = π

. Найти площадь S поверхно-

C

4

B x

сти вращения (рис. 3.30).

~

поверхно-

O

Найдем площадь S

сти, образованной вращением во-

A

круг

прямой

y = x

(прямой

x − y = 0 )

лепестка

OABCO лемни-

скаты. Ясно, что

S =

~

(в

силу

2S

симметрии). Лепесток OABCO оп-

Рис. 3.30. К вычислению площади

ределяется

уравнением

r = a

cos 2ϕ , ϕ

−

π

,

π

.

поверхности вращения в примере 6

4

4

dl =

r

2

2

dϕ =

a dϕ

, ϕ

−

π

,

π

(ϕ) +[r′]

ϕ

cos 2ϕ

4

4

(

.

Найдем расстояние ρ от точек

)

лемнискаты до прямой

x − y = 0 .

x (ϕ), y (ϕ)

Имеем

ρ =

a cos 2ϕ cos ϕ −a

cos 2ϕ sin ϕ

=

a

cos 2ϕ

cos ϕ −sin ϕ =

2

2

= a

cos 2ϕ (cos ϕ −sin ϕ) ,

π

2

так как cos ϕ −sin ϕ ≥ 0 , ϕ

,

π

−

4

. Следовательно,

4

130