Математический анализ определенный интеграл, несобственный интеграл, приложения определенного интеграла

~

π 4 a

cos 2ϕ

ϕ

2

π 4

S = 2π ∫

(cos ϕ −sin ϕ)

a d

=

2 πa

∫(cos

ϕ −sin ϕ) dϕ =

2

cos 2ϕ

−π 4

−π 4

=

2 πa2 (sin ϕ +cos ϕ)

π 4

= 2πa2 (кв. ед.).

~

−π 4

Значит,

S =

y

2S = 4πa2 (кв. ед.).

x2 + y2 = 2x

y=x

Пример

7.

Дуга

окружности

A

(меньшая π), отсекаемая прямой y = x , вращает-

ся вокруг этой прямой. Найти площадь S по-

верхности вращения (рис. 3.31).

(OA

представляется

уравнением

O

x

y =

2x − x2

,

x [0,1].

Из

соотношения

x2 + y2 = 2x

находим

2x +2 yy′

= 2

1− x

x

y′

=

1+( y′ )2 =

1

=

1

,

Рис. 3.31. К вычислению

y

y2

2x

− x2

x

x

площади поверхности

dx

dl =

1+( yx′ )2 dx =

,

x [0,1].

вращения в примере 7

2x − x2

(x, y ( x))

(OA до прямой

y = x (до прямой

Найдем расстояние ρ от точек

x − y = 0 ). Имеем

(

− x),

1

1

2

1

2

ρ =

2 x

− y (x) =

2 x

− 2x − x

=

2

2x − x

так как для x [0,1]:

2x − x2 − x ≥ 0 . Следовательно,

1

1 ( 2x − x2 − x)

dx

1

x

S = 2π∫

2 = 2 π∫

1−

2

dx =

0

(

2

2x − x

)0

0

2x − x

2

2

1

π

=

2 π

x +

2x − x

−arcsin (x −1)

=

2 π

2 −

(кв. ед.).

131

Рис. 3.32. К определению объема тела

§ 4. Вычисление объемов тел

1°. Понятие объема тела вводят совершенно аналогично тому, как было введено понятие площади плоской фигуры.

Пусть (T ) – некоторое пространственное тело, ограниченное поверхностью

~

(S ) . Заключим (T ) в прямоугольный параллелепипед (P ) , грани которого параллельны координатным плоскостям (рис. 3.32).

Пусть

z

a ≤ x ≤ b, (P ) = c ≤ y ≤ d,

e ≤ z ≤ h.

Произвольной сетью плоскостей, параллельных координатным плоскостям, разобьем (P ) на частичные па-

	(P )	раллелепипеды		(Pi jk )	( i =1, n ;
		j =1, m;	k =1, l ).	Обозначим через
	(T )	λi jk длину диагонали частичного па-
		раллелепипеда (Pi jk ) , а через λ – наи-
	y	большую	из длин	диагоналей этих
x		частичных		параллелепипедов
		( λ = maxi, j,k {λi jk }).		Произведенному

разбиению (P ) соотносим два числа

A и B:

A – сумма объемов всех тех частичных параллелепипедов (Pi jk ) , которые целиком содержатся в (T ) (они не имеют ни одной общей точки с поверхно-

~

стью (S ) , ограничивающей (T ));

B – сумма объемов всех тех частичных параллелепипедов (Pi jk ) , которые

имеют хотя бы одну общую точку с (T ) .

Ясно, что B = A +Q , где Q – сумма объемов всех тех частичных параллеле-

~

пипедов (Pi jk ) , которые имеют хотя бы одну общую точку с поверхностью (S ) . Заметим, что для закрепленного способа разбиения (P ) на части (Pi jk ) A и B – определенные числа. Если же способ разбиения (P ) на части (Pi jk ) изменить, то изменятся, вообще говоря, и числа A, B.

132

Рис. 3.33. К формулировке теоремы 2

Определение 1. Если существуют конечные пределы lim A и lim B , не за-

λ→0 λ→0

висящие от способа разбиения тела			) , и если lim	A = lim B (=V ) , то этот
	(T
			λ→0	λ→0

общий предел V называют объемом тела (T ) , а само тело (T ) называют куби-

руемым.

Теорема 1. Для того, чтобы тело (T ) было кубируемым, необходимо и достаточно, чтобы было

lim (B − A) = 0	( lim Q = 0 ).	(1)
λ→0	λ→0

Разности Q = B − A составляются каждый раз из чисел A и B, отвечающих одному и тому же способу разбиения (P ) на части (Pi jk ) .

Доказательство теоремы 1 совершенно аналогично доказательству соответствующей теоремы в теории площадей (см. §1).

~

Определение 2. Поверхность (S ) , замкнутую или нет, называют простой, если она разложима на конечное число частей, каждая из которых выражается хотя бы одним из уравнений вида:

1)z = f (x, y);

2)x = g( y, z) ;

3)y = h(x, z) .

При этом предполагается, что функции f ( x, y), g( y, z), h(x, z) непрерывны в

	соответствующих областях.
	Теорема 2 (о простой поверхно-		z
	~
	сти). Пусть (S ) – простая поверх-
	ность, содержащаяся в параллелепи-
	педе (P ) (рис. 3.33). Произвольной
	сетью плоскостей, параллельных ко-
	ординатным плоскостям,	разобьем
	(P ) на частичные параллелепипеды
	(Pi jk ) . Пусть Q – сумма	объемов	y
	всех тех частичных параллелепипе- x

дов (Pi jk ) , которые имеют хотя бы

~

одну общую точку с (S ) . Тогда

lim Q = 0 .

λ→0

Доказательство теоремы 2 аналогично доказательству теоремы о простой кривой (см. §1).

Следствие из теоремы 2. Тело (T ) , ограниченное простой поверхностью

~

(S ) , кубируемо.

133

2°. Объем тела вращения в прямоугольных координатах. Пусть (AB

кривой задана уравнением y = f (x) , x [a, b], a < b . Пусть f ( x) C([a, b]) и f ( x) ≥ 0 , x [a, b]. Рассмотрим криволинейную трапецию, ограниченную снизу осью Ox, сверху – графиком функции y = f (x) , а с боков – отрезками прямых x = a , x = b . Станем вращать эту криволинейную трапецию вокруг оси Ox. По-

~

лучим тело вращения (T ) . Поверхность (S ) , ограничивающая тело (T ) , состо-

y

B

ит из частей, определяемых уравнениями:

1) x = a ;

2) x = b ;

3)

z = ±

[

f ( x) 2 − y2 .

]

Заметим, что

z( x, y) C(

xy ),

где

A

D

a ≤ x ≤ b,

~

x

(Dxy )=

≤ y

≤ f (x).

Видим, что (S )

− f (x)

A

0

B0

– простая поверхность

)

имеет

тело (T

объем.

Выведем формулу для объема V тела

(T

) . Для этого:

a = x0 < x1 <K< xn = b

1)

точками

произвольным образом разбиваем проме-

Рис. 3.34. К вычислению объема тела

жуток

[a, b]

на

части

[xk , xk +1]

вращения

( k =

0, n −1

);

2) на каждом промежутке [xk , xk +1] как

на основании строим два прямоугольника с высотами mk и

Mk , где mk

– наи-

меньшее, а

Mk – наибольшее значение функции f (x)

на [xk , xk +1]

( mk

и Mk

существуют, так как f (x) C [x

k

, x

] ).

(

k +1 )

134

	y				Получим две ступенчатых фигуры. Одна
M k					из них,	образованная			прямоугольниками с
					основаниями ∆x0 , ∆x1, K, ∆xn−1 и с высо-
					тами,	соответственно,			M0 , M1, K, Mn−1 ,
mk					содержит в себе криволинейную трапецию
					A0 ABB0 . Другая,		образованная прямоуголь-
				x	никами с основаниями ∆x0 , ∆x1,					K, ∆xn−1 и
	xk			xk +1	высотами, соответственно, m0 , m1, K, mn−1 ,
					полностью содержится в криволинейной тра-
					пеции A0 ABB0 .
					При вращении вокруг оси Ox эти ступен-
					чатые фигуры образуют два ступенчатых те-
Рис. 3.35. К вычислению объема					ла. Ясно, что тело (T ) будет содержаться це-
					ликом в одном из ступенчатых тел и содер-
		тела вращения			жать внутри себя другое ступенчатое тело.
					Ступенчатое тело, содержащее в себе те-
ло (T ) , состоит из цилиндров с высотами ∆x0 , ∆x1, K,								∆xn−1 и радиусами ос-
нований		M0 , M1, K, Mn−1 , а ступенчатое тело, содержащееся в (T ) , состоит
из	цилиндров		с	высотами	∆x0 , ∆x1, K, ∆xn−1		и	радиусами		оснований
m0 , m1, K, mn−1 соответственно.
	Объем ступенчатого тела, содержащего в себе тело (T ) , равен

					n−1
πM02 ∆x0 + πM12 ∆x1 +K+ πMn2−1 ∆xn−1 = ∑πMk2 ∆xk .
					k =0
					) , равен
Объем ступенчатого тела, содержащегося в (T
					n−1
πm02 ∆x0 + πm12 ∆x1 +K+ πmn2−1 ∆xn−1 = ∑πmk2 ∆xk .
					k =0
		) будет справедливо неравенство
Для объема V тела (T
		n−1	n−1
π ∑mk2 ∆xk ≤V ≤ π ∑Mk2 ∆xk .						(2)
		k =0	k =0

Замечаем, что обе суммы в неравенстве (2), являясь нижней и верхней суммами

Дарбу соответственно,			являются также интегральными суммами Римана для
функции π f 2 (x)							(	)
		в	промежутке [a, b] .		Так	как	f (x) C [a, b] ,		то и
(	)		(	)
π f 2 (x) C [a, b]			π f 2 (x) R [a, b]			lim σ	существует	и	равен
						λ→0

135

b

π∫ f 2 (x) dx . (Здесь λ = max {∆xk }.) Переходя в неравенстве (2) к пределу при

a

k =0, n−1

λ → 0 , получим

b
V = π∫ f 2 (x) dx .	(3)

a

Замечание. В формуле (3) S = πf 2 (x) есть площадь поперечного сечения тела (T ) плоскостью, перпендикулярной к оси Ox. Поэтому (3) может быть записана в виде

b
V = ∫S(x) dx .	(4)

a

В пункте 3° будет показано, что формула (4) оказывается верной и для объема V тела (T ) , которое не является телом вращения вокруг оси Ox, но кубируемо. Правда, тело (T ) должно быть еще таким, что известны площади S(x) его поперечных сечений плоскостями, перпендикулярными к оси Ox, причем

S(x) C([a, b]).

3°. Объем тела с известными площадями поперечных сечений. Рассмот-

рим кубируемое тело (T ) , располагающееся вдоль оси Ox между плоскостями x = a и x = b . Рассмотрим сечение этого тела плоскостью x = const , где x – любое из [a, b] . Площадь сечения S является функцией от x, определенной на промежутке [a, b] . S(x) предполагается непрерывной на отрезке [a, b] (рис. 3.36).

y

O

a (T ) x

b x

z

S (x )

Рис. 3.36. Тело (T ) с известными площадями поперечных сечений

Теорема 3. Объем кубируемого тела с известными площадями сечений S(x) плоскостями, перпендикулярными оси Ox, выражается формулой

b
V = ∫S(x) dx .	(5)

a

136

Основываясь на определении объема тела (T ) , разобьем параллелепипед (P ) , содержащий внутри себя тело (T ) , сетью плоскостей, параллельных координатным плоскостям, на частичные параллелепипеды. Составим из них ступенчатые тела ( A) с объемом A и (B ) с объемом B такие, что тело ( A) целиком содержится в (T ), а тело (B ) целиком содержит тело (T ) внутри себя. Вследствие кубируемости тела разбиение можно сделать настолько мелким, чтобы выполнялось неравенство B − A < ε, где ε – произвольно малое положительное

число. Пусть α(x)			и β(x) – площади поперечных сечений плоскостью
x = const тел (		) и	(				) соответственно. Это кусочно-постоянные функции.
	A				B
Для ступенчатых тел (						) и (			) формула (5) справедлива, т.е.
				A				B
							b			b
							A = ∫α(x) dx;			B = ∫β(x) dx .
							a			a

Так как эти интегралы сводятся к суммам объемов слоев, составляющих ступенчатые тела и лежащих между плоскостями разбиения, перпендикулярными оси Ox. Далее, очевидно, что выполняются неравенства для площадей

α(x) ≤ S(x) ≤β( x) .

Интегрируем их по промежутку [a, b] . Получаем

b	b			b
∫α(x) dx ≤ ∫S(x) dx ≤ ∫β(x) dx .
a	a			a
Запишем эти неравенства в виде
	b
	A ≤ ∫S(x) dx ≤ B .						(*)
	a
Кроме того, по смыслу построения тел (			) и (			) имеем неравенство
		A			B
	B ≥V ≥ A.						(**)
Вычитаем из неравенств (*) неравенства (**) почленно:

b

A − B ≤ ∫S( x) dx −V ≤ B − A.

a

Отсюда

b

−ε ≤ ∫S(x) dx −V ≤ ε.

a

b

Так как разность ∫S(x) dx −V есть число постоянное, а ε произвольно мало, то

a

эта разность равна нулю, т.е.

137

b

∫S(x) dx −V = 0 .

a

Отсюда следует доказываемая формула (5).

Пример

1. Объем

трехосного эллипсоида,

заданного уравнением

x2

+

y2

+

z2

=1.

a2

b2

c2

Вдоль оси Ox эллипсоид располагается между плоскостями

x = −a и

x = a . Уравнение эллипсоида перепишем в виде

y2

z2

=1−

x2

если

+

b2

c2

a2

x

< a , то

y2

+

z2

=1.

(b 1− x2 a2 )2

(c 1− x2 a2 )2

Из этого уравнения видим, что в сечении эллипсоида плоскостью

x = const

(

x

< a ) получается эллипс с полуосями b

1− x2

a2

и c 1− x2

a2 . Площадь

эллипса равна числу π, умноженному на произведение полуосей:

S( x) = π(b 1− x2 a2 )(c 1− x2 a2 )= πbc(1− x2 a2 ).

Тогда по формуле (5) находим

a

a

a

x2

x3

4

V =

∫

S(x) dx = 2πbc

1−

dx = 2πbc

x

−

=

3

πabc (куб. ед.).

a2

∫

3a2

0

−a

0

*Пример 2. Найти объем тела, ограниченного поверхностями x2 + y2 = ax ;

x+ z = 0 ; x − z = 0 .

138

z

z

D

x0 C x

A

y

B

~	z = x0	~
D		C

			y
~		z = −x0	~
A			B
y = − ax0 − x02		y = ax0 − x02

Рис. 3.37. К вычислению объема тела в	Рис. 3.38. Сечение тела в примере 2
примере 2

Отмечаем, прежде всего, что тело (T ) ограничено простой поверхностью,

аследовательно, оно имеет объем V. Пересечем тело (T ) любой плоскостью

x= x0 , где x0 – любое, принадлежащее (0, a) . В сечении получим прямоуголь-

ник ABCD (рис. 3.38), проекция которого на плоскость Oyz ограничена линия-

ми: z = −x0 ; z = x0 ; y = − ax0 − x02 ; y = ax0 − x02 . Имеем

~ ~

~ ~

AD

=

= 2x0

,

AB

=

= 2 ax0 − x02 .

AD

AB

Значит, площадь сечения тела плоскостью, перпендикулярной к оси Ox, будет равна

S( x0 ) = 4x0 ax0 − x02 , x0 (0, a) .

Тогда объем V тела (T ) будет равен

a

= a43 ∫

0

a

a

V = ∫S(x0 ) dx0 = 4∫x0 ax0 − x02 dx0 =

0

0

x0 =a

a2

a

1

2

2

= 4

−

−

x0 +

ax0

8

12

3

x0

− x0

x0 =0

d(x0 −a 2)

a3

2x0 −a x0 =a

(a 2)2 −(x0 −a 2)2 =

4 arcsin

a

x0 =0

	a3	a	dx
		∫
+	16				0	2		=
			ax		− x
		0		0		0

= a43 π2 + π2 = π4a3 (куб. ед.).

* Пример 3.			) , ограниченного поверхностями
	Найти объем тела (T
z2 = a (a − x − y);	x = 0 ; y = 0 ; z = 0 ( a > 0 ) (рис. 3.39).

139

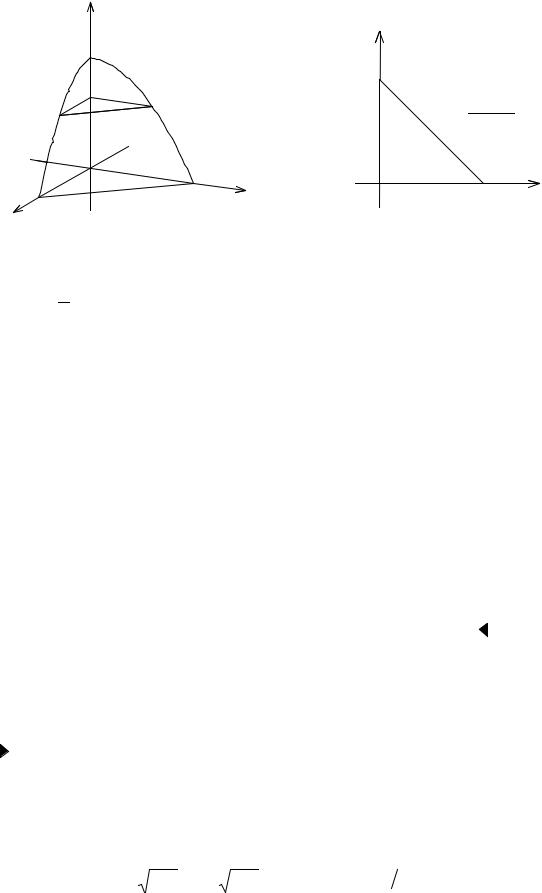
z			y
a
		~
C	B	B		a2	−z02
			x +y =
A					a
O	y				x
		~		~
x a	a
		C		A
Рис. 3.39. К вычислению объема тела в		Рис. 3.40. Сечение тела в примере 3
примере 3

Тело кубируемо, так как оно ограничено простой поверхностью. Пересечем тело (T ) плоскостью z = z0 , где z0 – любое, принадлежащее (0, a) . Получим в сечении треугольник ABC, проекция которого на плоскость Oxy ограни-

чена

линиями:

x = 0 ;

y = 0 ;

x + y =

a2

− z02

3.40). Имеем

a

(рис.

~ ~

=

~ ~

=

a2

− z2

Значит,

площадь сечения тела плоскостью, перпендику-

AC

BC

a

0 .

S( z0 )

1

a2 − z

2

2

z0 [0, a] . Тогда объем V те-

лярной к оси Oz, будет равна

=

,

2

a

0

) будет равен

ла (T

a

1

a

V = ∫S(z0 ) dz0 =

∫(a2 − z02 )2 dz0 =

2a2

0

0

1

5

z0 =a

4

=

a4 z

0

−

2 a2 z3

+

z0

=

a3 (куб. ед.).

2a2

5

15

3

0

z0 =0

* Пример

4.

Найти

объем

тела

) , ограниченного

поверхностями

(T

x2 +4 y2 = 8z ; x2 +4 y2 =1; z = 0 (рис. 3.41).

) кубируемо, так как оно ограничено простой поверхностью. Пе-

Тело (T

, где z

1

ресечем тело (T )

плоскостью z = z

0

0

0,

. Получим в сечении фигу-

8

ру, проекция которой на плоскость Oxy ограничена линиями:

	x2		+		y2		=1;	x2	+		y2			=1.
(	8z0 )	2		(	2z0 )	2		2		(		)	2
								1
										1 2

140