Математический анализ определенный интеграл, несобственный интеграл, приложения определенного интеграла

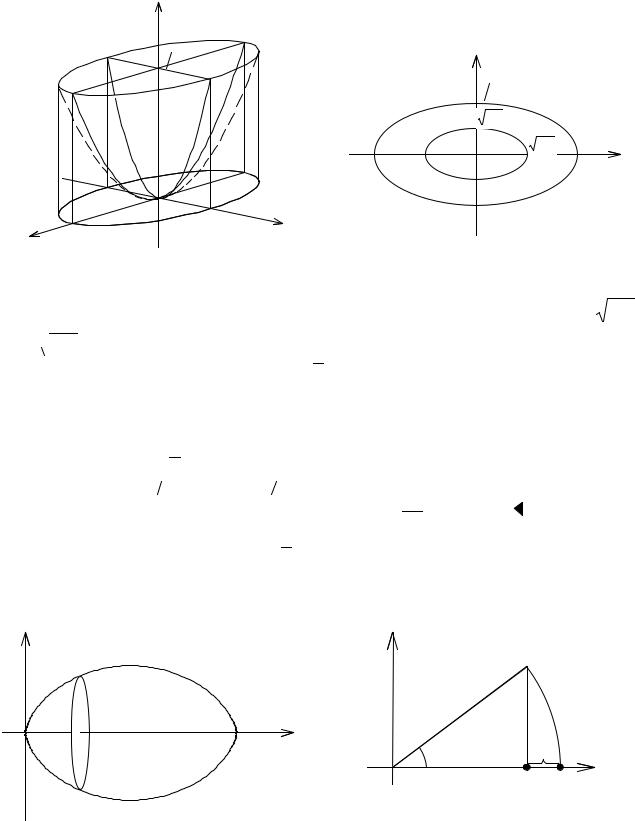
z

	1 8			z
				1 2
				2z0					x
				0		8z0
									1
x	y
Рис. 3.41. К вычислению объема тела в		Рис. 3.42. Сечение тела в примере 4
	примере 4				= 1
Это кольцо, ограниченное эллипсами с полуосями a			1	=1, b		;	a	2	= 8z	0	,
				1	2

b2 = 2z0 (рис. 3.42). Мы знаем, что площадь эллипса с полуосями a и b равна

πab . Поэтому площадь сечения тела (T ) плоскостью, перпендикулярной к оси Oz, будет равна

S( z

)

= π

1

−4z

, z

0,

1

.

0

0

0

2

8

Тогда объем V тела (T ) будет равен

V =

1 8

) dz

1 8

1

−

4z

=

π

(куб. ед.).

∫

S( z

0

0

= π

2

0

dz

0

32

∫

0

0

Пример 5. Найти объем тела (T ) , которое образуется при вращении одной

x = a (t −sin t),

t

[0, 2π], вокруг оси Ox (рис. 3.43).

арки циклоиды

= a (1

−cos t),

y

y

y

O

π

x

2 a

ϕ

h x

R−h R

Рис. 3.44. К вычислению объема

Рис. 3.43. Тело вращения в примере 5

шарового сектора

141

2πa

В формуле V = π ∫y2dx сделаем замену переменной, положив

0

x = a (t −sin t). Когда x изменяется от 0 до 2πa , t изменяется от 0 до 2π. Будем

иметь, следовательно,

2π 2π

V = π∫a2 (1−cos t)2 a (1−cos t) dt = πa3 ∫(1−cos t)3 dt = 5π2a3 (куб. ед.).

0 0

Пример 6. Круговой сектор, ограниченный линиями y = 0 , y = x tg ϕ и частью окружности x2 + y2 = R2 , вращается вокруг оси Ox. Найти объем V образующегося при этом шарового сектора.

R−h

R

V =V1 +V2 = π ∫x2 tg2 ϕdx + π ∫( R2 − x2 ) dx =

0

R−h

= π tg2 ϕ x3

R−h + πR2 x

R

−

π x3

R

=

3

0

R−h

3

R−h

= π3 [tg2 ϕ ( R − h)3 +3R2h +( R − h)3 − R3].

Имеем cos ϕ =

R − h

cos2

ϕ = ( R − h)2

tg2

ϕ = h(2R − h)

. А тогда

R

R2

( R − h)2

π

[h(2R − h)( R − h) +3Rh

2

3

]

2

2

V =

3

− h

V = 3

πR

h (куб. ед.).

* 4°. Объем тела вращения в полярных координатах.

Пусть имеется плоская фигура, ограниченная линиями, уравнения которых в

полярной системе координат имеют вид ϕ = α,

ϕ =β ( 0 ≤ α <β ≤ π),

r = f (ϕ) ,

ϕ [α,β]. Пусть

(

)

и f (ϕ) ≥ 0 ,

ϕ [α,β]. Выведем формулу для

f (ϕ) C [α,β]

) , полученного от вращения этой фигуры вокруг полярной

объема V тела (T

оси, а именно, покажем, что

2

β

2

β

π∫r

3

sin

π∫

f

3

(6)

V = 3

ϕdϕ =

3

(ϕ)sin ϕdϕ .

α

α

Для этого разобьем промежуток [α, β] на части [ϕk ,ϕk +1] точками

α= ϕ0 < ϕ1 < ϕ2 <K< ϕn =β

ипроведем лучи ϕ = ϕk ( k =1, 2, K, n −1). Построим ломаную с вершинами в

точках A0 , A1, A2 , K, An . Точка Ak имеет координаты (ϕk , f (ϕk )). При вращении вокруг оси Op плоский многоугольник OA0 A1KAn образует тело, объем

~	λ = max ∆ϕk . Если существует	~	, не
которого обозначим через V . Пусть		lim V
		λ→0

зависящий от способа разбиения промежутка [α, β] на части, то этот предел бу-

142

y

An =B

ϕ=β

Ak +1 ϕ=ϕk+1

Ak ϕ=ϕk

A1

дем принимать за объем V тела, полученного от вращения криволинейной фигуры OAB вокруг оси

Op.

Рассмотрим			плоскую фигуру,
ограниченную			лучами				ϕ = ϕk ,
ϕ = ϕk +1 и	кривой					r = f (ϕ) ,
ϕ [ϕk ,ϕk +1],			k =					(см.
					0, n −1
рис. 3.46). У						(		)
	нас f (ϕ) C [α,β]
f (ϕ) C [ϕ		k	,ϕ	]		f (ϕ)
(				k +1 )

ϕ=α A0 =A

O

x ( p)

Рис. 3.45. К определению объема тела вращения в полярной системе координат

достигает	на	промежутке
[ϕk ,ϕk +1]	своих наименьшего mk

инаибольшего Mk значений.

Проведем две дуги окружности с центром в точке O и радиусами mk и Mk . Рассмотрим теперь два

(1) ) и (T

(2) ) , образованные вращением плоских фигур,

ограниченных

тела (T

k

k

лучами ϕ = ϕk ,

ϕ = ϕk +1 и дугами окружностей радиусов r = Mk и r = mk . Ясно,

)

)

(1) ) и содержит в себе тело

что k-ая часть (T

тела (T

содержится в теле (T

(2) ) ( k =

k

k

) , V (1)

). Следовательно, если V

– объем те-

(T

0, n −1

– объем тела (T

k

k

(1) ) ,

k

(2)

k

ла

V

–

объем тела

(T

r=f (ϕ)

(2)

k

k

) , то

имеет

место

нера-

ϕ=ϕk+1

(Tk

венство

V (2) ≤V

≤V (1)

k

k

k

( k =

).

Мы знаем (см.

0, n −1

mk

∆ϕ

пример 6), что объем шарово-

го сектора Vш.с. вычисляется

k

ϕ=ϕk

= 2 πR2 h ,

Mk

p

по

формуле

V

O

ш.с.

3

где h – высота шарового сег-

Рис. 3.46. К определению объема тела вращения в

мента,

принадлежащего шаро-

полярной системе координат

вому сектору, R – радиус ша-

2 πM 2 ( M

2

ра. Поэтому

V (1)

=

k

− M

k

cos ϕ

k +1

) −

πM 2

( M

k

− M

k

cos ϕ

k

) =

k

3

k

3

k

∆ϕ

=

2

πM

3

(cosϕ

−cosϕ

) =

4

πM

3

sin

ϕ

k

+ϕ

k +1 sin

k .

3

k

k

k +1

3

k

2

2

V (2)

= 2

πm2

(m

− m cos ϕ

k +1

) −

2

πm2

(m − m cos ϕ

k

) =

k

3

k

k

k

3

k

k

k

143

=

2

3

−cos ϕ

) =

4

3

ϕ

k

+ϕ

k +1 sin

∆ϕ

k .

3

πm (cos ϕ

k

k +1

3

πm sin

2

2

k

k

Отметим,

что

ϕ

<

ϕk +ϕk

+1

< ϕ

,

k =

,

т. е.

ϕk +ϕk +1

[ϕ

,ϕ

] .

k

k +1

0, n −1

k

k

+1

2

~

2

Пусть

~

=

max

sin ϕ,

min

sin ϕ.

Тогда

sin ϕk

sin ϕk =

[ϕk ,ϕk+1 ]

~

[ϕk ,ϕk+1 ]

(1)

≤

4

3

~

sin

∆ϕk

;

(2)

≥

4

3

sin

∆ϕk

. Получаем, следова-

Vk

3

πMk sin

ϕk

2

Vk

3

πmk

sin ϕk

2

тельно,

4

~

∆ϕk

4

~

∆ϕk

3

3

sin

≤Vk

≤

sin

,

k = 0, n

−1.

3 πmk

sin ϕk

2

3

πMk

sin ϕk

2

а, значит,

n−1

n−1

4

3

~

sin

∆ϕk

≤V ≤

4

3

~

∆ϕk

.

3

π∑mk

sin ϕk

2

3

π∑Mk

sin ϕk sin

2

k =0

k =0

Пусть функция

f (ϕ)

достигает своего наименьшего значения mk на промежут-

ке [ϕk ,ϕk +1]

в точке

ϕ**k ,

а наибольшего значения Mk

в точке

ϕ*k ( ϕ**k и

ϕ

*

[ϕ

,ϕ

]). По формуле Тейлора sin

∆ϕ

k =

∆ϕ

k

−

cos(θ∆ϕ

k

)

∆ϕ

3

k

k

k +1

2

2

6

2

k

. По-

этому предыдущее неравенство перепишется в виде:

2

π

n−1

f

3

(ϕ

**

~

∆ϕ

−

4

π

n−1

f

3

(ϕ

**

~

cos(θ∆ϕ

k

)

∆ϕ

k

3

≤V ≤

3

∑

k

)sin ϕ

k

k

3

∑

k

)sin ϕ

k

6

2

k =0

n−1

k =0

n−1

3

≤

2

π

f

3

(ϕ

*

~

∆ϕ

−

4

π

f

3

(ϕ

*

~

cos(θ∆ϕk )

∆ϕk

3

∑

k

)sin ϕ

k

k

3

∑

k

)sin ϕ

k

6

.

2

k =0

(

)

k =0

По условию,

f (ϕ) –

ограниченная существует число

f (ϕ) C [α,β]

L > 0

такое, что

f (ϕ)

≤ L , ϕ [α,β]. А тогда

4π

n−1

3

**

~

cos(θ∆ϕ )

∆ϕ

3

3

2

n−1

π

3

β

−α

) 2

∑

f

)sin ϕk

k

≤

πL

∑

∆ϕk

=

L (

3

(ϕk

6

2

k

36

λ

36

λ

→0 ,

λ→0

k =0

k =0

4π

n−1

3

*

~

cos(θ∆ϕ

k

)

∆ϕ

k

3

3

2

n−1

π 3

β−α

) 2

∑

f

≤

πL

∑

∆ϕk

=

L (

→0 .

3

(ϕk )sin ϕk

6

36

λ

36

λ

2

λ→0

k =0

k =0

Следовательно,

n−1

2

3

**

~

∆ϕk

+(б.м.в. при λ → 0)≤V ≤

3

π∑ f

(ϕk

)sin ϕk

k =0

2

n−1

3

*

~

≤

π∑ f

+(б.м.в. при λ → 0).

3

(ϕk )sin ϕk ∆ϕk

k =0

Имеем

144

2

n−1

3

**

~

=

3

π∑ f

(ϕk

)sin ϕk ∆ϕk

2

n−1

k =0

2

n−1

(

~

)

=

3

**

**

+

3

**

)

sin

**

∆ϕk

=

3

π∑ f

(ϕk )sin ϕk

∆ϕk

3

π∑ f

(ϕk

ϕk

−sin ϕk

k=

0

k =0

14444244443

=σ**

(обозначение)

~

~

n−1

+ϕ**

−ϕ**

= σ** + 23

π∑ f 3(ϕ**k ) 2 cos

ϕ

k

ϕ

k

k

sin

k

∆ϕk .

2

2

k =0

~

−ϕ

**

~

**

∆ϕ

Так как

sin

ϕ

k

k

≤

ϕk −ϕk

≤

k

, то

2

2

2

n−1

~

+ϕ**

~

−ϕ**

n−1

23

π∑ f 3

(ϕ**k ) 2 cos

ϕ

k

ϕ

k

23 πL3λ ∑∆ϕk

k

sin

k

∆ϕk

≤

=

2

2

k =0

2

k =0

=

πL3λ(β−α) →0 .

Следовательно,

3

λ→0

n−1

2

3

**

~

= σ

**

+(б. м. в. при λ → 0) .

3

π∑ f

(ϕk )sin ϕk ∆ϕk

k =0

Совершенно аналогично убеждаемся, что

2

n−1

3

*

~

2

n−1

3

*

*

π∑ f

∆ϕk =

π∑ f

+(б. м. в. при λ → 0).

3

(ϕk )sin ϕk

3

(ϕk )sin ϕk ∆ϕk

k =0

k=0

14444244443

Итак, получим

=σ*

(обозначение)

σ** +(б. м. в. при λ → 0) ≤V ≤ σ* +(б. м. в. при λ → 0) .

(7)

В этом неравенстве σ** и σ* – интегральные суммы Римана для интеграла

2	π	β	f 3(ϕ)sin ϕdϕ. Так как	2	πf 3(ϕ)sin ϕ C [α,β] , то		lim	σ** и lim σ* суще-
3		∫		3	(	)	λ→0	λ→0
		α

β

ствуют и равны 23 π∫α f 3(ϕ)sin ϕdϕ. Переходя в неравенстве (7) к пределу при

λ → 0 , получаем

V = 23			β
			π∫ f 3(ϕ)sin ϕdϕ.
			α
		) образовано вращением вокруг полярной оси фи-
Замечание. Если тело (T
гуры, ограниченной линиями:			ϕ = α, ϕ =β ( − π ≤ α <β ≤ 0 ), r = f (ϕ) , где

145

f (ϕ) C([α,β]) и f (ϕ) ≥ 0 , ϕ [α,β], то для объема V тела (T ) формула

β

V = − 23π ∫α r3 sin ϕdϕ.

~

Поэтому формулы (6) и ( 6) можно объединить в одну

β

V = 23π ∫α r3 sin ϕ dϕ.

справедлива

~

( 6)

(8)

От плоской фигуры, вращающейся вокруг полярной оси, требуется лишь, чтобы она была расположена по одну сторону от оси вращения.

Если окажется, что f (ϕ) ≤ 0 , ϕ [α,β], то вместо (8) следует пользоваться формулой

β			( 8 )
V = − 23π ∫r3 sin ϕ dϕ.
			~

α

Пример 7. Улитка Паскаля r = a +bcos ϕ вращается вокруг полярной оси. Определим объемы:

1)тела, ограниченного поверхностью вращения, когда a > b (рис. 3.47);

2)тела, ограниченного внешней поверхностью вращения, когда a < b (рис.

3.48);

3)полости между внутренней и внешней поверхностями вращения, когда

a < b .

	C	ϕ=ϕ0		C
B	A p	O	B	A
O			D	p

Рис. 3.47. К вычислению объема тела в примере 7. Случай a > b

Рис. 3.48. К вычислению объема тела в примере 7. Случай a < b

Заметим, что фигура симметрична относительно полярной оси.
1) В случае a > b она имеет вид, изображенный на рис. 3.47.		(ACB кривой
соответствует изменению ϕ от 0 до π,	f (ϕ) > 0 , ϕ [0, π]. Поэтому
π	π
V = 23 π∫r3 sin ϕdϕ = 23 π∫(a +bcos ϕ)3 sin ϕdϕ =
0	0

146

2

π

= −

π∫(a +bcos ϕ)3 d (a +bcos ϕ) =

3b

0

ϕ=π

= −

2π

(a +bcos ϕ)4

= 4

πa (a2 +b2 ) (куб. ед.).

3b

4

ϕ=0

3

2) В случае a < b

улитка Паскаля имеет вид, изображенный на рис. 3.48.

(ACO кривой соответствует изменению ϕ от 0 до ϕ

0

( π < ϕ

0

< π); (ODB

2

кривой соответствует изменению ϕ от ϕ0

до π; f (ϕ) ≥ 0 , ϕ [0,ϕ0 ], и f (ϕ) ≤ 0 ,

ϕ [ϕ0 , π]. Угол

ϕ0 определяется

из

соотношения

a +bcos ϕ0 = 0

cos ϕ0 = −a b.

Объем тела, ограниченного внешней поверхностью вращения (то есть поверхностью, образованной вращением (ACO ), будет равен

	ϕ0		ϕ0
V = 23 π ∫r3 sin ϕdϕ = 23 π ∫(a +bcos ϕ)3 sin ϕdϕ =
	0		ϕ=ϕ0	0
= − 2π (a +bcos ϕ)4				=	π	(a +b)4	(куб. ед.).
					6b
3b	4		ϕ=0

Обозначим через V* объем тела, ограниченного внутренней поверхностью вращения (то есть поверхностью, образованной вращением (ODB ). Имеем

f (ϕ) ≤ 0 , ϕ [ϕ0 , π]. Поэтому
V = − 2		π π r3 sin ϕdϕ = − 2			π π (a +bcosϕ)3 sin ϕdϕ =
*	3	∫	3				∫
		ϕ0				ϕ0
	= 2π (a +bcos ϕ)4			ϕ=π	=		π	(a −b)4	(куб. ед.).
							6b
	3b	4		ϕ=ϕ0
3) Объем V полости между внутренней и внешней поверхностями вращения

равен разности объемов тела, ограниченного внешней поверхностью, и тела, ограниченного внутренней поверхностью вращения:

V = 6πb (a +b)4 − 6πb (a −b)4 = 43 πa (a2 +b2 ) (куб. ед.).

5°. Вычисление объемов тел, ограниченных поверхностями, полученными от вращения кривых вокруг произвольных осей.

Пример 8. Найти объем тела, ограниченного поверхностью, полученной вращением дуги параболы y2 = 4ax около прямой y = 2x (рис. 3.49).

147

	y			y
		~		~
2a		x		x
				M 1
~			~
y
			y	M 2
		α		x
		x
	O	a		O

Рис. 3.49. К вычислению объема тела в		Рис. 3.50. Элемент объема тела вращения
примере 8		в примере 8
Сделаем преобразование координат		~
	~
x = x cosα − y sin α,
	~	~

y = x sin α + y cos α,

так, чтобы ось вращения стала осью абсцисс новой системы координат. У нас

tg α = 2 cos α =1

5

, sin α = 2

5

. Поэтому

1

~

~

x =

5

( x

−2 y ),

1

~

~

y =

5

(2x + y ).

Уравнение параболы в новой системе координат будет таким:

1

~

~

2

4a

~

~

5

(2x

+ y )

=

5

( x

−

2 y )

x [0, a 5

].

~

~

+2 5

a)+

~

+20a

2

,

y = −2

(x

2 5 5 ax

(Из двух знаков перед радикалом нужно взять знак “+”, так как интересующая нас дуга параболы лежит выше оси Ox~ .)

Для объема V тела будем иметь

a 5~2 ~	= π	a 5	~	+20a	2	)+4	~2	~	+20a	2	)−
V = π ∫y dx		∫[4	(5 5 ax				(x	+4 5 ax

0		0
~	+2	5 a)
−8(x

~		2	~		770 5		3
5 5 ax	+20a		]dx	=	3	πa		−8πJ ,

a	5	~	+2 5 a)	~	+20a	2 ~
где J =	∫(x			5 5 ax		dx .
	0

148

~

2

~

t −20a2

~

dt

~

В J сделаем замену 5

5 ax

+20a

= t

x

=

; dx

=

;

x

= 0

5

5 a

5 5 a

2

~

2

соответствует t = 20a

,

= a

5 соответствует t =

45a

. Получим

x

45a2

t −20a2

dt

802 5

3

J = ∫

5 5 a

+2 5

a

t

5 5 a

=

25

a

.

Следовательно,

20a2

V =

770

5

−

6416 5

πa

3

=

2

5

πa

3

(куб. ед.).

3

25

75

Приведенный здесь метод решения задачи является универсальным. Однако часто более удобным оказывается другой метод. Этот метод называется методом выделения элементов. Его смысл можно уяснить здесь на примерах 8, 9.

Находим расстояние ρ от произвольной точки (x, f ( x)) параболы до прямой y = 2x . Имеем

ρ =

2x − f ( x) = 2x −2

ax ,

x [0, a].

5

5

πρ2 dl (рис. 3.50). Здесь

Элемент dV

объема тела вращения будет равен

dl =

M1 M2

– высота, ρ

–

радиус

основания

цилиндра.

Имеем

dl = 1+( y′ )2

dx , где

y = 2x

и,

следовательно,

dl =

dx .

Значит,

5

x

ax )2

dV = π

(2x −2

5

5 dx . Тогда

∫a (x −

V = 4π

ax )2 dx = 2

5 πa3

(куб. ед).

5

0

75

x

y

Пример 9. Кривая

+

y

=1 вращается вокруг

a

b

b

прямой

x

+

y

=1.

Найти объем тела,

ограниченного

a

b

поверхностью вращения (рис. 3.51).

x

a

Рис. 3.51. К вычислению объема тела в примере 9

Из уравнения кривой

x

+

y

=1

следует, что

a

b

2

0 ≤ x

≤ a,

, и

−

x

. Расстояние

должно быть

≤ b,

y = b 1

0 ≤ y

a

ρ

от

произвольной

точки

этой

кривой

до прямой

x

+

y

=1 будет таким:

a

b

149

x

x

2

+ 1

−

−1

a

ρ=

a

=

2ab

x

−

x

,

x [0, a].

1

1

a2 +b2

a

a

+

a2

b2

x

dl =

1 +( y′ )

2

dx ,

y = b

Имеем далее

где

1

−

. Следовательно,

x

a

dl = 1 + b2

dx =

a2 +b2

dx . Для элемента

dV объема тела вращения будем

a2

a

иметь

2

2

dV = πρ2dl = π

4a

2

b

2

−

x

a

2

+b

2

4πab

2

(

)

x

dx =

x −

x

dx .

a

2

+b

2

2

a

a

a

a2 +b2 a

a

Поэтому

a

4πab2

x

x

2

2 πa2b2

V =

a2 +b2

∫ a −

a

dx =15

a2 +b2

(куб. ед.).

0

§5. Вычисление статических моментов и координат центров масс плоских кривых и плоских фигур

Определение. Пусть M – материальная точка массы m, Ox – некоторая ось, d

– расстояние от точки M до оси Ox. Тогда Sx = m d называют статическим мо-

ментом точки M относительно оси Ox.

При рассмотрении нескольких материальных точек M1, M2 , K, Mn с массами

m1, m2 , K, mn соответственно оказывается по-

лезным приписывать соответствующим расстояниям определенные знаки. По этой причине момент Sx , например, вводят в рассмотре-

ние только тогда, когда точки M1, M2 , K, Mn

расположены в плоскости, содержащей ось Ox. В этом случае через точку O проводят координатную ось Oy, перпендикулярную оси Ox, и под d понимают координату y точки M, так что

Sx = m y .

y

M

x

O

Рис. 3.52. К определению статического момента материальной точки

150