Метод итераций Теоретические основы метода

Пусть дано уравнение (1.1). Необходимо определить приближенный корень с заранее заданной точностью .

Будем считать, что корни отделены, т.е. определен отрезок (отрезки), содержащий строго один корень.

Допустим, уравнение (1.1) удастся представить в эквивалентном виде

x = (x), (1.4)

где (x) - некоторая непрерывная в [a, b] функция.

В качестве начального приближения выберем произвольную точку x₀ из [a, b] (x₀[a, b]) и подставим в правую часть уравнения (1.4), вычислим и найденное значение примем в качестве первого приближения x₁ = (x₀). Найденное первое приближение x₁ вновь подставим в правую часть уравнения (1.4), вычислим и найденное значение примем в качестве второго приближения x₂ = (x₁). Аналогично на шаге с номером n получим

x_n = (x_n-1). (1.5)

В результате описанной выше итерационной процедуры получим числовую последовательность приближений x₀, x₁, x₂, …, x_n, …. При n эта последовательность может либо иметь конечный предел, либо бесконечный предел, либо предела может не существовать вообще.

Допустим, что этот предел конечен, т.е.

, (1.6)

где  - конечное число.

Выясним, к чему стремится предел последовательности при n. В соотношении (1.5) слева и справа перейдем к пределу при n:

,

(*) – теорема о предельном переходе под знаком непрерывной функции: если функция непрерывна в точке, то знак предела и функции можно менять местами, т.е.

 = (). (1.7)

Соотношение (1.7) показывает, что число  обратило уравнение (1.4) в верное равенство и, следовательно, является корнем.

Соотношение (1.6) имеет место при выполнении неравенства

(1.8)

для любых x[a, b], где q - число.

Таким образом, если выполняется неравенство (1.8), то имеет место конечный предел (1.6) и, следовательно, упомянутая выше числовая последовательность, найденная итерационным путем, стремится к точному корню задачи (1.4), а в силу эквивалентности – и задачи (1.1).

Попытаемся уравнение (1.1) привести к виду (1.4) так, чтобы было выполнено условие сходимости (1.8).

Всегда можно предположить, что внутри отрезка [a, b] производная

. (1.9)

Действительно, если внутри [a, b] отрицательна, то достаточно от исходной задачи (1.1) перейти к эквивалентной задаче -f(x) = 0, для которой первая производная будет уже положительна.

Таким образом, всегда можно допустить положительность производной внутри [a, b].

Пусть m - наименьшее, M - наибольшее значения в [a, b].

Обе части уравнения (1.1) умножим на произвольное число , получим эквивалентное уравнение

 f(x) = 0,

или

x – x +  f(x) = 0.

Тогда

.

В последнем уравнении правая часть зависит от произвольного числа  и аргумента x. Попытаемся выбрать  таким образом, чтобы было выполнено условие сходимости (1.8). Имеем

.

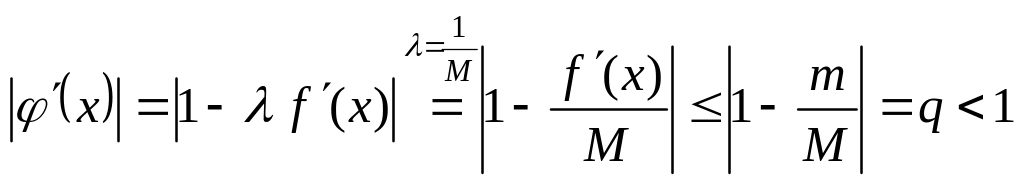Таким образом, если выбрать , то для приведенной выше функции  выполняется неравенство (1.8).

Итерационную процедуру следует прекратить на шаге с номером n при выполнении неравенства

и в качестве приближенного решения задачи принять число x_n.