Метод итераций для решения слау

Теоретические основы метода

Метод итераций для решения СЛАУ рассмотрим на примере системы, состоящей из трех уравнений с тремя неизвестными

(3.1)

Требуется определить приближенные решения системы с заданной точностью .

Аналогично методу Гаусса, будем предполагать, что

a_ii  0, i = 1,2,3.

Систему (3.1) приведем к виду, удобному для итераций. Для этого выразим неизвестные, лежащие на главной диагонали:

(3.2)

Введем обозначения:

Тогда система (3.2) перепишется:

(3.3)

В качестве нулевого приближения можно принять произвольную тройку чисел. Например:

Здесь и в дальнейшем верхний индекс обозначает номер итерации.

Выбранные нулевые приближения подставим в правую часть системы (3.3), вычислим и найденные значения примем в качестве первого приближения:

Найденные первые приближения вновь подставим в правые части системы (3.3), вычислим и найденные значения примем в качестве второго приближения:

Рассуждая аналогично, на итерации с номером n получим

(3.4)

Соотношения (3.4) и есть расчетные формулы метода итераций для СЛАУ.

Приведенная итерационная процедура является сходящейся к точному решению при выполнении следующего условия: в матрице коэффициентов А максимальные по модулю элементы для каждой строки должны находиться на главной диагонали. Выполнение этого свойства может быть обеспечено путем суммирования и перестановки уравнений. Заметим, что это свойство является достаточным, но не необходимым.

Описанную итерационную процедуру следует прекратить на итерации с номером k при выполнении неравенства

и в качестве приближенного решения задачи принять числа .

Заметим, что из соотношения (3.4) следует, что каждое последующее приближение вычисляется с использованием значений предыдущей итерации.

Метод Зейделя

Теоретические основы метода

Метод Зейделя является разновидностью метода итераций, но обладает более быстрой сходимостью по времени за счет того, что некоторые приближения текущей итерации вычисляются с использованием значений, вычисленных на той же итерации. Расчетные формулы метода имеют вид

Вопросы сходимости и достижения заданной точности метода Зейделя тождественны аналогичным вопросам метода итераций.

Лабораторная работа № 4 Приближенные методы вычисления определенных интегралов

Порядок выполнения работы

Работа выполняется в два этапа:

а) вычисление числа интервалов n разбиения отрезка интегрирования при заданной точности  ;

б) вычисление значения определённого интеграла с заданной точностью .

I. Вычисление числа интервалов разбиения отрезка интегрирования:

а) для получения задания обратитесь к преподавателю или нажмите кнопку ВАРИАНТ;

б) в ячейке А9 (голубая ячейка) укажите точность;

в) вычислите число интервалов n и укажите в ячейке А10;

г) в ячейку А6 введите формулу, содержащую Вашу подынтегральную функцию и использующую в качестве аргумента х ссылку на адрес А7.

2. Вычисление значения определённого интеграла с заданной точностью  :

а) в ПОЛЕ ДЕЯТЕЛЬНОСТИ (голубые ячейки) внесите расчётные формулы метода;

б) в ячейку G9 внесите формулу, ссылающуюся на адрес из ПОЛЯ ДЕЯТЕЛЬНОСТИ, содержащий решение задачи;

в) для проверки правильности выполнения этапа нажмите кнопку РЕЗУЛЬТАТЫ.

Общие теоретические основы методов

Пусть необходимо вычислить определённый интеграл с заранее заданной точностью 

, (4.1)

где пределы интегрирования a и b, подынтегральная функция f(x) заданы.

Если первообразную функции f(x) удастся представить в конечном виде, то нет необходимости в использовании численных методов, а достаточно использовать формулу Ньютона-Лейбница. Поэтому в дальнейшем речь пойдет о функциях f(x), первообразную которых невозможно представить в конечном виде.

Формула трапеций

Теоретические основы метода

Пусть задана функция f(x) и некоторый отрезок [a, b], причем для любого x[a, b]

f(x)  0. (4.2)

П ри выполнении условия (2) значение интеграла (1) совпадает с площадью криволинейной трапеции, ограниченной осью ОХ, вертикальными прямыми x = a и x = b и графиком функции y = f(x). Вычислим эту площадь с заданной точностью .

Отрезок [a, b] разобьем на n частей длиной . При этом получим n+1 граничную точку, т.е.

a = x₀ < x₁ < x₂ < … < x_n = b, x_i = x₀ + i h, i=1,2,…, n+1.

В каждой граничной точке восстановим перпендикуляр до пересечения с графиком функции, точку пересечения назовем узлом. Соединим отрезком прямой каждую пару близлежащих узлов, при этом получим n обычных трапеций. Сумма площадей этих трапеций отличается от площади криволинейной трапеции не более чем на заштрихованную область на рис.1. Поэтому для искомой площади криволинейной трапеции можно приближенно записать

,

где S_i - площадь трапеции с номером i. Тогда

Последнее соотношение есть формула трапеций для приближенного вычисления площади криволинейной трапеции и, следовательно, рассматриваемого интеграла. Точность вычислений возрастает при увеличении числа n. Требуемая точность вычисления будет достигнута при выполнении неравенства

; .

При невыполнении условия (4.2) полученная формула также может быть использована в силу того, что приведённые выше рассуждения совпадают по содержанию с интегральной суммой определённого интеграла.

Элементарная формула Симпсона (парабол)

Теоретические основы метода

Вычислим определённый интеграл от функции f(x) = x² +  x +  в пределах от x = a до x = b.

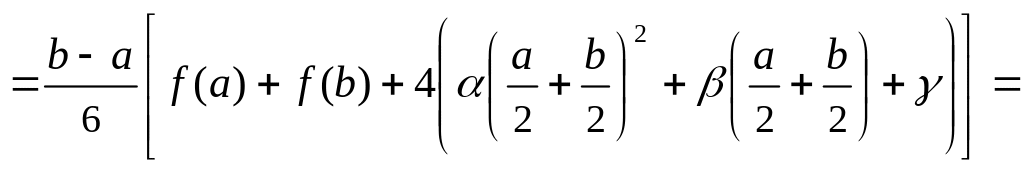
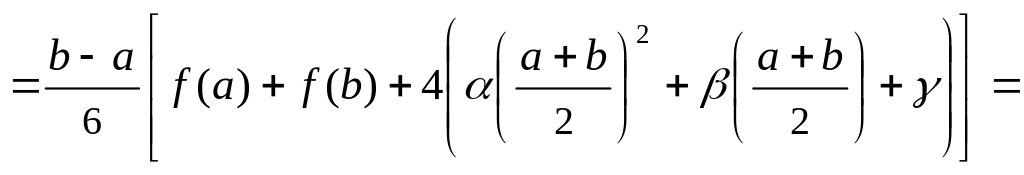
Обобщенная формула Симпсона (парабол)

Теоретические основы метода

Пусть необходимо вычислить с заданной точностью .

Отрезок [a, b] разобьем на n отрезков одинаковой длины . Причем n - четное число. После разбиения отрезка получим n+1 граничную точку, т.е. a = x₀ < x₁ < x₂ < … < x_n = b, x_i = x₀ + i h, i=1,2,…, n+1.

В каждой точке разбиения восстановим перпендикуляр до пересечения с графиком функции y = f(x), в результате получим n+1 узловую точку пересечения и пар близлежащих отрезков.

В методе трапеций внутри каждого отрезка разбиения подынтегральная функция была приближенно представлена в виде отрезка прямой f(x)  ax+b. В данном методе подынтегральная функция внутри каждой близлежащей пары отрезков заменяется квадратичной зависимостью: f(x)  (x)=x² + +. Тогда рассматриваемый интеграл приближенно можно представить с учетом элементарной формулы Симпсона в виде

Последнее соотношение есть обобщенная формула Симпсона для вычисления определенного интеграла.

Заданная точность  будет достигнута при выполнении неравенства

; .

Формула Симпсона обладает более высокой точностью при фиксированном числе n по сравнению с формулой трапеций в силу того, что, как известно из курса математического анализа, чем выше степень полинома, тем точнее этот полином аппроксимирует рассматриваемую функцию.