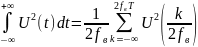2.2.2. Свойства функций отсчетов.

Для любых целых k и n:

Следовательно:

Формула 1:

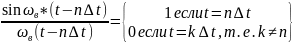
Следовательно, в моменты отсчетов функция 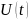превращается в сами отсчеты .

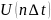Ортогональность – ни одна из базисных функций не выражается через комбинацию других функции.

Представление исходной функции в виде Формулы 1 ряда Котельникова является представлением ее в виде разложения по базисным функциям.

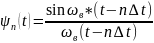– базисная n-ая функция.

Эти функции называются функциями отсчетов.

Рис 3.

Ширина главного лепестка функции отсчета на нулевом уровне равна .

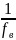Относительно своего максимума каждая функция симметрична. В моменты эти функции стремятся к 0.

Все функции отсчета ортогональны между собой на бесконечно большом промежутке времени, что математически выражается следующим образом:

Формула 2:

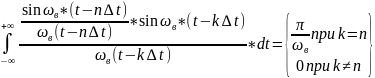
Определение ортогональности.

Докажем ортогональность: введем в Формулу 2 следующие обозначения:

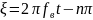
Формула 3:

Произведение синусов раскладываем в косинусы и раскладываем на простейшие множители:

Формула 4:

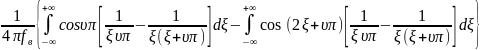
Первый интеграл из Формулы 4 равен 0, что и докажем далее.

Для доказательства этого мы разбиваем его на два слагаемых и вводим:

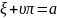
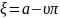
Так как:

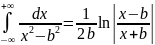
Переходим ко второму интегралу:

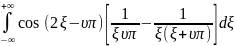
Подставим в интеграл:

Следовательно, получится:

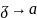
Под интегралом разность косинусов превращается в произведение синусов:

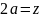
Формула 4:

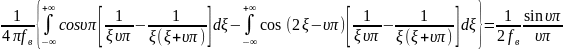
Для целочисленных значений 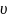это выражение равно 0 при .

Ортогональность доказана.

2.2.3. Первое следствие теоремы Котельникова.

Чтобы передать по каналу связи сообщение, представляющее собой непрерывную функцию времени , имеющую спектральное ограничение частотой необходимо проделать следующие операции:

1. Произвести отсчеты мгновенных значений передачи сообщений в моменты времени отстоящие друг от друга на .

2. Передать по каналу связи эти величины каким-либо методом.

3. Восстановить на приемнике переданные отсчеты и сформировать импульсы, амплитуды которых были бы равны или пропорциональны переданным отсчетам, а длительности были бы достаточно малыми по сравнению с : .

4. Сформировать функции отсчетов, амплитуды которых были бы равны или пропорциональны переданным отсчетам Хорошее приближение к этим функциям можно получить на выходе фильтра с полосой пропускания и постоянным коэффициентом передачи, если на вход фильтра подавать кратковременные импульсы , амплитуды которых пропорциональны отсчетам.

Рис 4

2.2.4. Второе следствие теоремы Котельникова.

С помощью теоремы Котельникова можно получить энергию сигнала через его отсчеты.

Формула 1:

– квадратичный эффект сигнала

Чтобы определить энергию через отсчеты по Котельникову, мы должны вернуться к ряду Котельникова:

Ряд Котельникова:

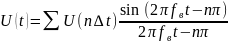
Подставим Ряд Котельникова в Формулу 1 и получим:

Формула 2:

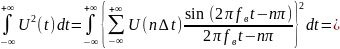
Квадрат суммы под интегралом можно представить в виде произведения:

Формула 3:

Это выражение можно представить в виде одной двойной суммы:

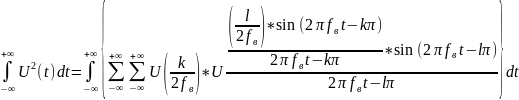
Изменим порядок интегрирования и суммирования и учтем, что отсчеты не зависят от t:

Формула 4:

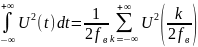
Мощность сигнала – сумма квадратов его отсчетов.

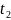
Если сигнал ограничен во времени и существует в промежутке времени от до 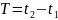(т.е. сигнал финитный, конечный), то количество отсчетов оказывается конечным и равным:

Формула 5:

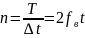
В этом случае мы получим конечное количество слагаемых. Кроме того, энергия сигнала не зависит от начала координат.

Совместим этот сигнал с моментом времени 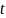, и тогда квадратичный эффект выразится: