4.2.2. Теорема Шеннона для дискретного канала без помех.

Определение: Если пропускная способность дискретного канала без помех превышает производительность источника сообщений, т.е. если

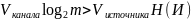
то существует способ кодирования и декодирования сообщений источника с энтропией , обеспечивающий сколь угодно высокую надежность отождествления принятых комбинаций с действительно переданными.

Если же , то такого способа нет.

Для доказательства все типичные последовательности достаточно большой протяженности 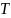будем кодировать цифровыми кодовыми комбинациями из множества 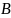той же протяженности с основанием алфавита , равное объему алфавита канала.

При этом число символов (разрядность цифрового кода) равно .

Тогда число :

Число типичных последовательностей длительности может быть определено как:

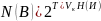
Условие теоремы можно записать как равенство:

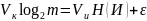
где - любая малая величина.

Откуда получаем, что :

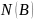Пусть 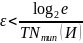, тогда:

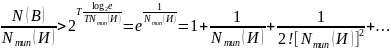
Отбрасывая все члены начиная с третьего в правой части неравенства мы переходим к следующему виду:

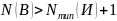
Итак, при выполнении условий теоремы число различных кодовых комбинаций , по крайней мере на 1 больше, чем число типичных последовательностей, подлежащих кодированию.

Эту избыточную кодовую комбинацию мы поставим в соответствие всем нетипичным последовательностям, предопределив их недостоверную передачу.

Поскольку при 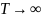и , вероятность нетипичной последовательности стремится к 0, а величина , определяющая превышение пропускной способности канала над производительностью источника, бесконечно мала, то первая часть теоремы доказана.

При нарушении условия теоремы, когда , используя тот же путь доказательства, мы получим, что

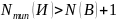
Т.е. в этом случае даже при описанном способе кодирования, обеспечивающим равную вероятность использования всех символов алфавита канала, и скорости передачи канала мы не сможем передать все типичные последовательности, исходящие от источника.

Оптимальное кодирование, использованное при доказательстве теоремы Шеннона для дискретного канала, сводится к предельному укрупнению алфавита канала, когда каждая укрупненная кодовая комбинация соответствует бесконечно длинной последовательности символов от источника сообщения.

При этом, одновременно устраняется корреляция между символами укрупненного алфавита, и, благодаря сохранению только типичных последовательностей, обеспечивается равная вероятность их появления. В результате устраняется избыточность сообщения, переданного по каналу.

Кодирование способом, изложенным при доказательстве теоремы, связано с задержкой сообщения на время:

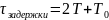
где - задержка на технические операции (кодирование, декодирование, проход по каналу и т.д.).

В канале без помех источником ненадежности отождествления переданных комбинаций с принятыми могут быть только сами операции, ибо нарушения в канале не происходят, т.к. канал без помех.

4.2.3. Скорость передачи информации и пропускная способность дискретного канала с помехами.

В канале без помех среднее количество информации, получаемой с выхода канала в единицу времени, соответствует среднему количеству информации, содержащемуся во входном сообщении, той же длительности.

В канале с помехами это соответствие нарушается. Здесь скорость передачи информации будет меньше среднего количества информации, поступающего на вход канала в единицу времени, потому что часть информации разрушается помехами.

Помехи нарушают взаимнооднозначное соответствие между символами 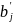на входе и на его выходе.

Принятый символ на выходе канала определяет не какой-то конкретный , а некоторый закон распределения апостериорных вероятностей

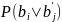
Если алфавит состоит из 0 и 1, то

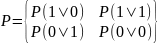
Апостериорная энтропия входного сообщения после приема конкретного символа равная в канале без помех нулю, при наличии помех будет неравна 0.

Осредним апостериорную энтропию сообщения по всем возможным символам :

Формула 1

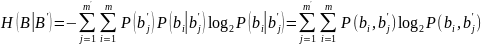
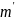- алфавит на входе, может быть не равно – алфавит на выходе

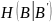- средняя потеря информации при передаче одного произвольного символа по каналу (ненадежность канала).

Вспомним их теории вероятностей:

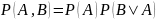
Формула Баеса

Формула Баеса позволяет определять условные вероятности 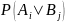, например, характеризующие правдоподобность той или иной гипотезы об исходе непосредственно наблюдаемого явления при известном исходе явления 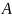, если только известны 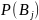в сочетании с любым из исходов явления 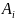, и, кроме того, известна .

Формула 1 с использованием формулы Баеса можно записать следующим образом:

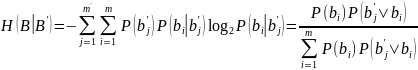
Из полученной формулы видно, что ненадежность зависит как от статистических характеристик входного сообщения канала, так и от вероятностных характеристик искажений символов вносимых действиями в канале с помехами. Эти помехи могут задаваться матрицей условных переходов

Среднее количество информации, приходящееся на один символ канала с помехами, определяется уменьшением неопределенности знания переданного символа после приема.

Это уменьшение равно разности априорной и апостериорной энтропии переданного сообщения:

Формула 2

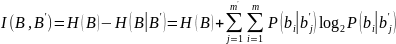
Двойной аргумент в 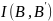означает, что осреднение информации приходящееся на 1 символ должно производиться по всем сочетаниям символов входного и выходного алфавита.

Рассмотрим две группы зависимых событий:

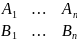
каждая из которых составляет полную группу событий, причем несовместных событий.

В этом случае полная вероятность события , т.е. вероятность того, что вообще произойдет совместно с каким-либо событием , будет равна:

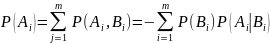
Преобразуем Формулу 2 , используя последнюю формулу и формулу полной вероятности.

В силу симметрии канала связи относительно входного и выходного алфавита можно заключить следующее:

Отсюда видно, что среднее количество информации о текущем состоянии входного сообщения заключенного в одном символе входного и наоборот одинаковы и представляется, как разность априорной и апостериорной энтропии.

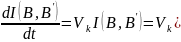
Под пропускной способностью дискретного канала с помехами будем понимать предельно возможную скорость передачи информации при заданных технических характеристиках канала (мощность алфавита, и , скорость передачи и ненадежность канала). Она соответствует условию максимума среднего количества информации на один символ, т.е. условию безызбыточности входного сообщения.

Формула 3

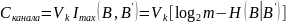
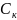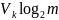определяется как предельное количество информации, которое достигает выхода канала в единицу времени, если на его вход поступает максимальное количество информации , которое только может воспринять канал на входе.

Из Формулы 3 следует, что зависит от ненадежности канала.

При отсутствии помех ненадежность равна 0:

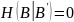
Т.к. при

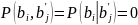
А при

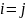
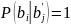
В этом случае

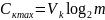
Когда канал полностью забит помехами, т.е. независимо от выходного символа равновероятен любой символ на входе