1) А, где а – точка, являющаяся вершиной угла;

2) Вас, где а – точка, являющаяся вершиной угла, в и с – точки, взятые на разных сторонах угла (ав и ас – лучи, образующие угол);

3) (Ab), где a, b – лучи, образующие угол.

Если стороны угла являются дополнительными полупрямыми, то угол называется развернутым. Его градусная мера равна 180.

Угол с градусной мерой 90 называется прямым. Угол с градусной мерой меньше 90 называется острым, а угол с градусной мерой больше 90, но меньше 180 называется тупым.

Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.

Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, называется касательной.

Теорема.

Касательная к окружности имеет с ней только одну общую точку, точку касания.

Дано: окружн-(О), а - касательная

Доказать, что т А - единственная) 1.Пусть касательная и окружность имеют кроме т А, общую т В, отличную от А.

Рис. 4б

2. Тогда, ∆ АOВ – равнобедренный, т к АО=ОВ=R.

3.т к ∆ АOВ- равнобедренный, то у него А =В

4. т к ОА а, то ОАВ=90,  ОАВ=АВО=90 т е у ∆ АOВ два прямых угла, это невозможно

Билет 9

Измерение углов основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус – угол, равный 1/180 части развернутого угла. 1/60 часть градуса называется минутой, а 1/60 часть минуты называется секундой.

Опр1. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла.

Равные углы имеют равные градусные меры .

Для измерения углов используется транспортир.

Аксиома измерения углов:

Каждый угол имеет положительную градусную меру. Градусная мера угла равна сумме градусных мер двух углов, на которые он делится некоторым лучом, лежащим внутри угла.

Опр1. Окружностью называется геометрическая фигура, состоящая из всех точек, плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.

Опр2. Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, называется касательной к окружности.

Теорема 1 (об отрезках касательных, проведенных к окружности из одной точки). Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Д ано: О – окружность; p и q – касательные;

p∩q ={A}; n – луч; O n.

Доказать: AB = AC; OAB = OAC.

Доказательство:

1. По свойству касательных осq, obp. Проведем луч из точки а через центр окружности. 2. Рассмотрим образовавшиеся треугольники аос и аов.

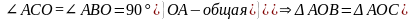
прямоугольные по гипотенузе и катету.

3. Из

4. Из

Билет 10

Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а общее начало лучей – вершиной угла

Опр 1. Две угла называются равными, если они имеют одинаковую градусную меру.

Опр2. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

OC – биссектриса. COB = AOС = AOB.

Аксиома откладывания углов:

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и притом только один.

.

Опр1. Треугольник называется вписанным в окружность, а окружность – описанной около треугольника, если все вершины треугольника лежат на окружности.

Теорема 1. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров.

Дано:  АВС; KK1, NN1, PP1 -

серединные перпендикуляры.

Доказать: KK1 ∩ NN1 = {O};

KK1 ∩ PP1 = {O}.

Доказательство: