38. Сходимость знакопеременных рядов. Абсолютная и неабсолютная (условная) сходимость знакопеременного ряда.

Сходимость произвольных рядов.

Ряды, в которых имеется бесконечное количество положительных членов и бесконечное количество отрицательных членов, называют знакопеременными.

Ряды знакочередующиеся: . Здесь полагаем все . В таком ряде знаки + и - чередуются и идут через один, откуда и название ряда.

Для рядов с произвольным распределением знаков можно установить только достаточный признак, когда вопрос о сходимости можно свести к изучению сходимости положительного ряда.

Итак, изучаются ряды , где - величины положительные и отрицательные.

Теорема. Если сходится ряд, составленный из абсолютных величин его членов: , то и данный ряд также сходится.

Действительно, обозначим положительные члены ряда . Ряд сходится, т.к. его частичные суммы монотонно возрастают и ограничены сверху суммой ряда . Также сходится ряд, составленный из отрицательных : , т.е. сходится ряд . Тогда , где . При Поэтому существует предел - ряд сходится.

Определение. Если ряд сходится вместе с рядом , то говорят, что имеет место абсолютная сходимость ряда . Если же ряд сходится, а ряд расходится, то говорят о неабсолютной, или условной, сходимости ряда . Примеры: - абсолютно сходящийся ряд. Далее: - не абсолютно сходящийся ряд (условно сходящийся ряд).

Переместительное свойство абсолютно сходящихся рядов.

Если ряд сходится абсолютно, то сходится (также абсолютно) и ряд , полученный произвольной перестановкой членов исходного ряда.

Существенно отметить, что перестановке могут подвергаться бесконечное множество членов исходного ряда.

Докажем. Пусть сначала имеем знакоположительный ряд , т.е. для всех n , a_n>0. Так как по нашему условию он сходится, то можно писать =S₀, S₀ – определенная величина. Рассмотрим k -ую частичную сумму ряда : . Очевидно, . Обозначим N=max(n₁,…,n_k). Тогда имеем очевидное неравенство: , ибо среди членов частичной суммы S_N есть и члены . Но S_N  S₀ при любом N. Итак, при любом k имеем . Следовательно, частичные суммы ряда не только монотонно возрастают, но и ограничены сверху. Следовательно, последовательность имеет предел при k, то есть ряд сходится. При этом для его суммы имеет место неравенство: . Далее, меняя (в рассуждениях ) ряды и местами, можно доказать и неравенство: . Откуда получаем единственно возможное и непротиворечивое равенство: - суммы у рядов и одинаковые.

Если ряд абсолютно сходится, то абсолютно сходится и ряд .

39.Два свойства неабсолютно сходящихся рядов

1. Можно показать, что если ряд сходится неабсолютно, то ряд, составленный из одних только положительных его членов P: и ряд, составленный из одних только отрицательных его членов Q: расходятся (не сходятся). Подчеркнем, что p_k есть положительное , а q_k есть , причем здесь само - отрицательное. Поясним кратко причину такого свойства условно сходящегося ряда.

Ибо если сходится ряд P и сходится ряд A: , то имеем: ( ), где - частичные суммы рядов A, P и Q соответственно. Нам известно, что существуют пределы последовательностей и , следовательно, существует и предел последовательности . Но тогда существует и предел суммы ,

т.е. сходится ряд , чего нет на самом деле. Следовательно, ряды из только положительных членов и из только отрицательных членов условно сходящегося ряда расходятся, несмотря на то, что и при .

2. На этом основании можно доказать второе вышеупомянутое свойство условно сходящихся рядов (теорему Римана): в условно сходящемся ряде можно так переставить члены, что его сумма будет равна любому наперед заданному числу B.

Например

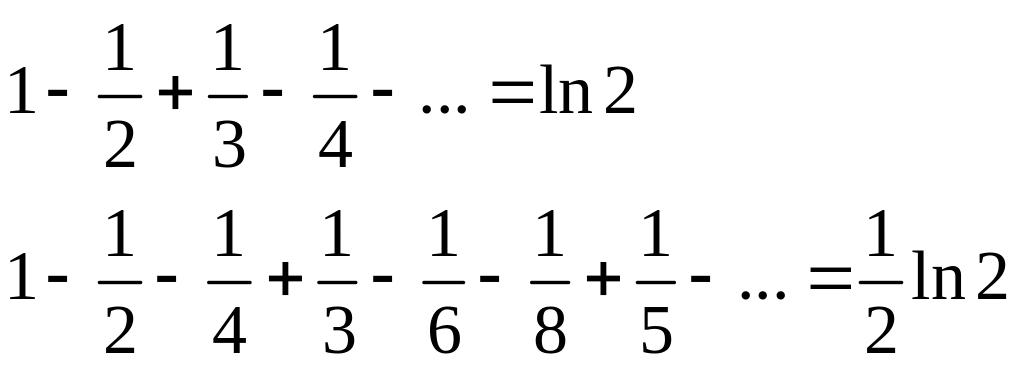
Наметим путь доказательства теоремы: Задаем число B. Из ряда берем сначала только положительные члены в таком количестве, чтобы выполнилось неравенство: . Затем берем отрицательные члены ряда : (все q <0) в таком количестве, чтобы было неравенство в другую сторону: . Процесс прибавления новых положительных и новых

отрицательных членов повторяем неограниченно. Уклонение получающихся сумм (фактически частичных сумм ряда с переставленными членами) от числа В не превосходит или , k – достаточно большое. Следовательно, с ростом k уклонение новых частичных сумм от числа В стремится к нулю, так что сумма нового ряда, составленного из членов ряда , будет равна В, что и требуется доказать в теореме Римана.