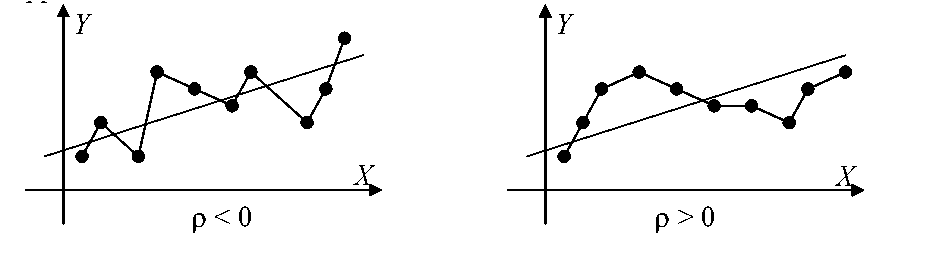8. Оценка существенности (значимости) линейной регрессии

После того как найдено уравнение лин. регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости ур-я регрессии дается с пом. F- критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен 0, т.е. b =0, и, фактор X не оказывает влияния на результат y.

Непосредственному расчету F- критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной Y от среднего значения на две части — «объясненную» и «необъясненную».Если фактор не оказывает влияния на рез-т, то Ŷ=Y дисперсия рез-та не зависит от регрессора, т.е. остаточная дисперсия=0.

Любая сумма квадратов отклонений связана с числом степеней свободы, кот. показывает сколько независимых отклонений из n возможных [(Y_l-Y),(Y₂-Y),...,(Y_n-Y)] требуется для образования данной суммы квадратов. Для общей суммы квадратов требуется (n-1) независимых отклонений. При расчете объясненной или факторной суммы квадратов используются теоретические (расчетные) значения результативного признака , найденные по линии регрессии . В линейной регрессии (1). Это следует из ф-лы лин. Коэффициента корреляции

из которой получим: r²=b²σ_x²/σ_y², т.е. сумма квадр. отклонений, обусловленных лин. регрессией, запишется как (1). Поскольку при заданном объеме наблюдений по X и по Y факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы.

Существует рав-но между числом степеней свободы общей , факторной, остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии сост. n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, т.е. df_общ=n-1.

Если поделить каждую сумму кв. отклонений на соот-ее ей число степеней свободы, получим средний квадрат отклонений, т.е. дисперсию на одну степень свободы.

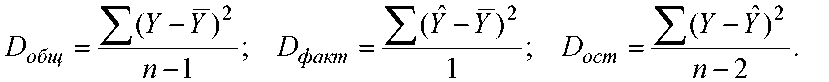
Эти дисперсии явл. сравнимыми. Величина F=D_факт/D_ост наз. критерием Фишера. Если нулевая гипотеза H₀ справедлива, то факторная и остаточные дисперсии не отличаются друг от друга. Альтернативная гипотеза H₁ будет справедлива , если факторная дисперсия превышает остаточную в несколько раз. Для оценки исп. Табл. Критических значений F-отношений при различных уровнях значимости и различном числе степеней свободы. Если полученная в результате числовой обработки результатов эксперимента F_факт>F_табл, то гипотеза H₀ отклоняется. В противном случае уравнение регрессии считается статистически незначимым.

9. Природа ошибок регрессии. Основные гипотезы для обоснования парной линейной регрессионной модели

1 ° Y_t=а+bX_t+ε_t, t=l,...,n — спецификация модели. ε_t – ошибка измерения

2° X_t — детерминированная величина; вектор х=(Х₁,...,Х_n)' не коллинеарен вектору i=(1,...,1), т.е. не все х одинаковы.

За° E(ε_t)=0; 3b° Е(ε_t²)=σ² — не зависит от t.

4° E(ε_t*ε_s)=0 при t≠s, некоррелированность ошибок для различных наблюдений

Часто добавляется условие

5° Ошибки ε_t имеют совместное норм. распределение с мат. ожиданием=0 и дисперсией= σ².

В этом случае модель называется классической нормальной линейной регрессионной.

Зам. В случае норм. Линейной регрессионной модели условие 4° эквивалентно условию статистической независимости ошибок ε_t и ε_s.

Реальные модели не «обязаны» соблюдать эти условия, обсудим условия 1° - 4° и их возможные нарушения.

Условие 1° указывает на спецификацию модели, как парной лин. регрессии. Возможно, что на результативный признак оказывает не одна, а несколько переменных. В этом случае получаем модель множественной регрессии. Если же хоть один из регрессоров входит в заданную модель нелинейно, то имеем модель нелинейной регрессии

Условие 2° означает, что не все регрессоры одинаковы. При невыполнении этого условия никакой реальной регрессионной модели построить невозможно.

Условие За° E(Y_t)=a+bX_t т.е. при фиксированном X_t среднее ожидаемое значене Y_t =а+bX_t.

Условие 3б° (гов. о независимости дисперсии ошибки от номера наблюдения) гомоскедастичность. Отклонение от этого условия наз. гетероскедастичностью.

Условие 4° указывает на некоррелированность ошибок, для простых величин выполняется практически всегда; но для временных рядов это условие часто нарушается, т.е. имеет место автокорреляции ошибок.