10. Теорема Гаусса-Маркова для парной линейной регрессии.

Пусть мы имеем набор данных (наблюдений) (X_t,Y_t), t=1,…,n и выполняются условия:

1 ° Y_t=а+bX_t+ε_t, t=l,...,n — спецификация модели. ε_t – ошибка измерения

2° X_t — детерминированная величина; вектор х=(Х₁,...,Х_n)' не коллинеарен вектору i=(1,...,1), т.е. не все х одинаковы.

За° E(ε_t)=0; 3b° Е(ε_t²)=σ² — не зависит от t.

4° E(ε_t*ε_s)=0 при t≠s, некоррелированность ошибок для различных наблюдений

Задача: оценить «наилучшим» способом a, b и σ². Термин «наилучший» означает, что найти в классе лин. (по Y_t) несмещенных оценок наилучшую в смысле мин. дисперсии.

Зам. Если такая оценка найдена, то это не означает, что не существует нелинейной оценки с меньшей дисперсией.

Теорема Гауса-Маркова. При справедливости 1°-4° оценки и (*) имеют наим. дисперсию в классе всех лин. несмещенных оценок.

Доказательство.

1. Проверка несмещенности МНК-оценок . Используя , получим

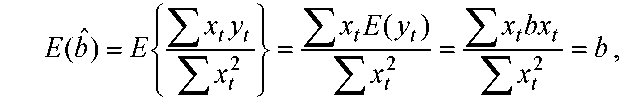
А из (*)=>

2. Оценим дисперсии aˆ, bˆ: (1)

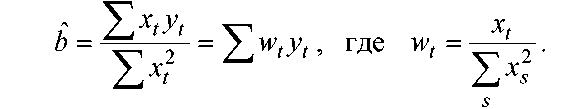
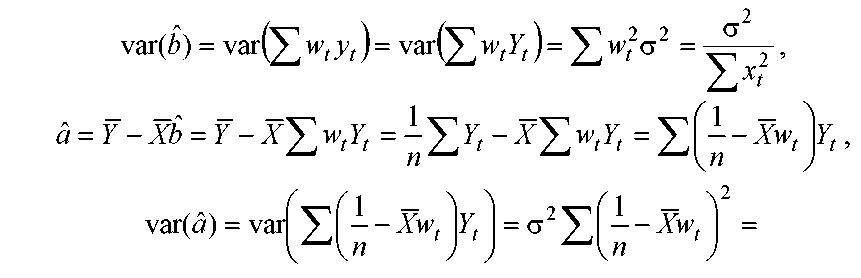( 2)

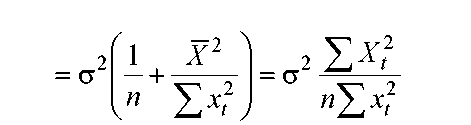
(3)

Используя (1) и (3) можно показать, что

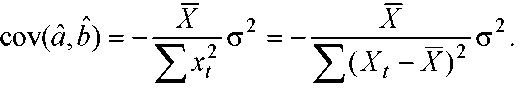
(4)

Зам. Из (4) => cov(a^,b^)<0.

3. Покажем, что МНК-оценки явл. «наилучшими» в классе всех лин. несмещенных оценок.

Пусть =Σc_tY_t — любая другая несмещенная оценка. Пусть c_t=w_t+d_t, тогда

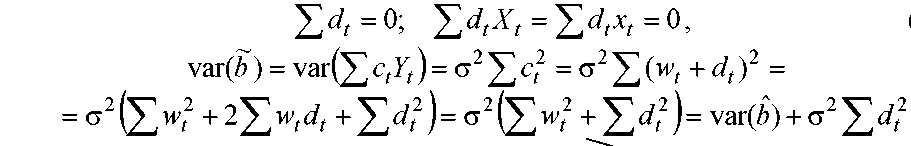справедлива для всех a и b, если

Т.е. var(b) > var(b^), ч.т.д.