44.Сравнение б/б:

в основу сравнения кладётся lim их отношений

если (1)=const≠0,то А(x),В(x)-б/б одного порядка если (1)=0,то А(x)-б/б более низшего порядка

если (1)=∞,то А(x)-б/б высшего порядка

если (1)=1,то А(x),В(x)-эквивалентные б/б

45.Ф-ия y=f(x)-непрерывна в (·) x₀ если:1.она определена в некот окр-ти этой (·),2.сущ f(x),3.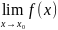 =f(x0); Зам-е: послед два пункта означ,что lim справа=lim справа=знач ф-ции в (·).

Ф-ция назыв непрерыв в обл-ти, если она непрерывна в каждой (·) этой обл-ти.

Ф-ция y=f(x) назыв непрерыв в (·) x₀ если бесконеч малому приращ арг-та соответ бесконеч малое приращ ф-ции.

46.Множ-во (·), в кот наруш условие непрерыв назыв (·) разрыва ф-ции.

1. если хотя бы один из односторон lim не сущ или =∞, тов этой (·) ф-ция терпит разрыв второго рода.

2. если оба односторон lim конечны, но ≠ между собой и<∞, то это неустранимый разрыв первого рода.

3. если оба lim конечны, равны между собой, но не совпадают со знач ф-ции в (·)x₀, то ф-ция терпит устранимый разрыв первого рода.

47.Св-ва ф-ций непрерыв на отрезке.

Т-ма1(Вейерштрасса): если ф-ции f(x) и g(x) непрерыв в (·)x₀, то ф-ции: f(x)±g(x), f(x)·g(x), f(x)/ g(x) также непрерыв. Док-во:воспользов определением непрерыв ф-ции на языке ε,δ-окрестности: ε>0 δ>0: x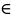 U_δ(x₀) |f(x)-f(x₀)|< ε

Т-ма2: если ф-ция f(x) непрерыв в (·)x₀ и f(x₀) ≠0, то сущ δ-окр-ть в (·)x₀ такая, что: U_δ(x₀), : U_δ(x₀) f(x)≠0

Т-ма3: если f(x) непрерывна в замкнутой, огранич обл (Ū) то она огранич в этой обл,т.е.: M>0: Ū f(x)‌|≤M

Т-ма4: пусть ф-ция u=φ(x)непрерывна в (·)x₀, а ф-ция y=f(u), U₀= φ(x₀), тогда y=f(φ(x)) непрерывна в (·)x₀.

Т-ма5(Вейерштрасса): пусть f(x) непрерывна в Ū, тогда f(x) достигает в этой обл-ти своё наиб и наим знач.

Т-ма6(Коши): пусть ф-ция f(x) непрер в Ū и m-наим, а M-наиб значения этой ф-ции, тогда для любого ξ [m,M] (·)x₀ Ū:f(x₀)=ξ,т.е. она принимает все знач между наиб и наим. Сл-е: пусть ф-ция y=f(x) непрерыв в обл U,если сущ (·)x₁ и (·)x₂ U:f(x₁)<0,f(x₂)>0 (·)x₀ U: f(x₀)=0

48.Производная. Осн опред и геом смысл.Производной y =f(x) по аргументу x назыв lim отношения приращения ф-ции к приращ аргумента при стремлении последнего к 0 произвольным образом: y'(x₀)= = Зам-е:1.произв ф-ции в (·)-это число,а произв на отрезке-ф-ция.2.при определ произв обычно считают,что lim конечен, однако, если lim сущ и =∞,то в этой (·) ф-ция имеет бесконеч произв.

Геом.смысл: знач произв f '(x₀)=tgα угла наклона касат,образов ею с осью ох в этой (·).Ур-е касат:y=f(x₀)+f '(x₀)(x-x₀). Если материал(·) перемещ во времени по закону y=s(t)-путь,то s'(t)=ds/dt=v-мгнов скорость.

49. Производная. Осн опред и геом смысл.Производной y =f(x) по аргументу x назыв lim отношения приращения ф-ции к приращ аргумента при стремлении последнего к 0 произвольным образом: y'(x₀)= = Зам-е:1.произв ф-ции в (·)-это число,а произв на отрезке-ф-ция.2.при определ произв обычно считают,что lim конечен, однако, если lim сущ и =∞,то в этой (·) ф-ция имеет бесконеч произв.

Производительность труда -производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной. Пусть y(x)-функция, характеризующая, издержки производства, где x - количество выпускаемой продукции. Тогда отношение y(x)/x описывает средние издержки, приходящиеся на одно изделие. Среднее приращение, средний прирост, средняя скорость изменения определяется отношением ∆y/∆x . Производная y'=lim∆y/∆x выражает предельные издержки производства. Отношение ∆y/∆xy называется темпом прироста функции y. Отношение y'(x)/y(x) называется мгновенным темпом прироста.

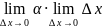50.Связь между непрерыв и диф-тью.Т-ма1:если ф-ция y=f(x) диф-ма в (·)х₀, то она в этой (·) непрерыв. Док-во: т.к. f(x)- диф-ма в (·) х_0, тогда по т-ме о lim: ∆y/∆x=f '(x₀)+α(∆x),где α 0. ∆y=f '(x₀)∆x+α(∆x)·∆x = = f '(x₀) + .Т.к. y непрерывн в (·) х_0.

51.Правила дифференцирования суммы, произведения и частного двух диф-мых функций. Т-ма:если функции u=u(x) и v=v(x) имеют в (·)x производные, то сум (разн), произвед и частн этих функций также имеют производные в этой (·), и справедливы следующие формулы:1.(u±v)'=u'±v', 2.(u·v)'=u'v+v'u, 3. (u/v)=(u'v−v'u)/v². Док-во: из определения производной: (u±v)'= = = ± =u'±v'

(u·v)'= = + =uv'+vu'.

(v/u)'= = =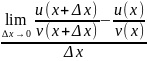

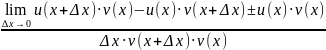52.Проивз сложн ф-ции:Т-ма:пусть дана ф-ция y=f(x),кот можно выразить в виде y=F(u),где u=φ(x),т.е. y=F(φ(x)),тогда если ф-ция y=φ(x)-диф-ма в (·)х_0, а F(u)-диф-ма в (·)u₀= φ(x₀), то y= F(φ(x))-диф-ма в (·)х₀ при этом y'_x=F'_u·φ'_x=y'_u·u'_x Док-во:т.к. ф-ции φ и F-диф-мы след-но непрерыв в (·) х₀ и u₀ соотв зададим аргум x бесконеч малое приращ ∆x,кот вызовет бесконеч малое приращ ∆u и ∆F. ∆x ⇒∆u=u(x₀+∆x)-u(x₀)⇒∆F=F(u₀+∆u)-F(u₀) ; u+∆u=u(x₀+∆x), y+∆y=F(u₀+∆u). Рассморт =y'_u ⇒ =y'_u+α(∆u)-б/м при ∆u , ∆y=y'_u·∆u·α(∆u)·∆u, ∆y/∆x=y'_u·∆y/∆x+α(∆u)∆y/∆x. = y_u(∆u/∆x)+α(∆u/∆x)]=y'_u + =y'_u·u'_x+0+u'_x= y'_u·u'_x

53.Произв обрат ф-ции:Замеч: 1.возр и убыв ф-ции имеют одну произв, 2.если ф-ция непрерыв на промеж[a,b]причем f(a)=c,f(b)=d то обрат ф-ция будет определ на промеж[c,d],3.графики взаимнообр ф-ций симметр относит биссектр 1 и 3 коорд углов,4.если ф-ция не явл ни возраст,ни убыв,то она может иметь несколько обрат ф-ций. Т-ма:если для ф-ции y=f(x) сущест обратная ф-ция x=φ(y),кот в рассмотрен (·) имеет произв x'=φ'(y) отличную от 0,то в этой (·) ф-ция y=f(x) имеет произв=f'x=1/φ'(y). Док-во: рассмотр x=φ(f(x)), x'=[φ(f(x))]'=φ'y·f'x=f'x=1/φ'y

54.Показ-степен ф-ей назыв ф-ция вида y=u^v,где u=u(x),v=v(x).Т-ма: если y=u^v,то y'=u^v·lnu·v'+v·u^v-1·u' Док-во:рассмотр y=u^v-прологарифм обе части, lny(x)=ln u^v-продиф-м, (lny(x))'=(v'(x)lnu+v(lnu(x))'·((1/y)·y')=v'lnu+v(1/u)u', y'=y(v'lnu+v(1/u)·u'), y'=u^v(v'lnu+(v/u)·u'), y'= u^v·v'·lnu+v·u^v-1·u'

55.Диф-ал ф-ции: ∆y=f '(x₀)·∆x+α(∆x)·∆x, f '(x₀)-главн линейн часть приращ ф-ции- диф-л, обознач df(x) или dy, df(x)= f '(x)∆x, ∆x-приращ аргум. Геом смысл:Диф-л ф-ции=приращ ординаты касательной к граф ф-ции y+f(x) на промеж ∆х. dy(x₀)=f'(x₀)∆x=tgφ·∆x Рисунок

56. Диф-ал ф-ции: ∆y=f '(x₀)·∆x+α(∆x)·∆x, f '(x₀)-главн линейн часть приращ ф-ции- диф-л, обознач df(x) или dy, df(x)= f '(x)∆x, ∆x-приращ аргум. f'(x)=dy/dx-запись произв. В приближ вычисл часто польз равенством: ∆y≈dy⇒f(x+∆x)≈dy+y(x). Пример:y=sin31,(·)x₀=30, sin30=1/2, ∆x=1=π/180, sin31≈cos30∆x+sin30= /2·π/180+1/2. Правила вычисл: dc=0, d(u±v)=du±dv, d(cu)=c·du, d(uv)=du·v+dv·u, d(u/v)=(du·v-dv·u)/v²

57. Произв n-1 порядка от ф-ции f(x) назыв произв первого п-ка от произв n-1 п-ка: y⁽ⁿ⁾=(y^(n-1))'. Обознач:y'',y''',y^VII,y⁽³⁰⁾. Правила диф-я произв высш п-ка:1.(u±v)⁽ⁿ⁾=u⁽ⁿ⁾±v⁽ⁿ⁾,2.(cu)⁽ⁿ⁾=c·u⁽ⁿ⁾,3.(uv)⁽ⁿ⁾=∑c^k_nu^(n-k)v^k,4.c^k_n=n!/(k!(n-k)!). Диф-лом n-го п-ка назыв диф-л от диф-ла n-1 п-ка: dⁿy=d[dⁿy]=[f^(n-1)(x)dx^n-1]'dx=f⁽ⁿ⁾(x)dxⁿ.d²f=f ''(x)dx²,d³f=f '''(x)dx³. Пример: y=x⁶, d²x=30x⁴dx²,d³x=120x³dx³. Обознач:y⁽ⁿ⁾=dⁿy/dxⁿ.Замеч: для сложной ф-ции y=F(u(x))…dy=F'udu тогда d²y=F''udu²=d[dF]=(F'udu)'du=F_uu''(du)²+F'ud²u. Механич смысл второй произв:пусть матер (·)М перемещ прямолин по з-ну y=s(t),тогда втор произв от пути по времени есть ускорен прямолин движ-я: a(t)=d²s/dt²=s''(t)

58. Ф-ция наз параметр.задан если её аналитич задание имеет вид: ,t₀≤t≤t_N. Пусть задана зависим двух перемен x и y от парам-ра t, изменяющ в пределах α и β: α≤t≤β, Пусть ф-ция x=φ(t) имеет обратную t= φ^-1(t)=Ф(x).Тогда y=ψ(t)=ψ(Ф(x))⇒y-сложн ф-ция. Зависимость y от x, заданная через зависим каждой из них от параметра t в виде x=φ(t),y=ψ(t), назыв ф-ей,задан парам-ки. Будем считать, что ф-ции Ф,ψ,φ- диф-мы,тогда Ф_x'(x)=1/φ'(t), то y_x'=dy/dx=ψ'(t)/φ'(t)=y_t'(t)/x_t'(t). Пример: , y_x'=dy/dx=y_t'/x_t'=cost/-sint=-ctgt

59. Эластичн ф-ции Ф-ция f(x) достигает в (·)х₀ лок-го минимума(мак-ма) если существует ок-ть этой (·) u(x₀)=( x₀-δ,x₀+δ): х=U(x₀), f(x)≥(≤)f(x₀).

Лок-ный мин(макс) назыв лок экстрем. Эластичн ф-ции - предел отношения относительного приращения функции y (зависимой переменной) ∆y/y относительному приращению независимой переменной x ∆x/x, при Δx и Δy→ 0, выражается формулой: E_x(y)=x/y· dy/dx. Э. ф. является мерой реагирования одной переменной величины на изменения другой.

60. Необход услов экстрем Лок-ный мин(макс) назыв лок экстрем. Необход услов экстрем (Т-ма Ферма): если ф-ция y=f(x) имеет производную в (·)x₀ и достиг в этой (·) лок-го экстремума, то f '(x₀)=0. Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками.

61. Теорема Роля.

Теорема Роля: если y=f(x) непрерывна на [a;b] и дифференцируема на (a;b), приэтом f(a)=f(b), то существует такая (.)ξ, принадлежащая (a;b).

Док-во:

1) пусть f(x) – const. тогда для любой (.)ξ, принадлежащая (a;b) => f’(ξ)=0.

2) пусть f(x) const. тогда [a;b] – замкнутый и ограниченный => по т.Вейерштрасса в силу непрерывности ф-ии f(x)=y, сущ. (.) x₁, x₂, принадлежащие [a;b] такие, что f(x₁) – наименьшее значение ф-ии, а f(x₂) – наибольшее значение ф-ии.

f(x₁) ≠ f(x₂) (иначе f(x) – const.)

(.) x₁, x₂ не могут быть одновременно концами отрезка [a;b], т.к. f(a)=f(b) => какая-то из этих точек (ξ) попадает внутрь (a;b). В (.)ξ f(x)=y достигает локального экстремума => по т.Ферма f’(ξ)=0. ч.т.д.

Замечания:

1) т.Роля сохраняет силу и на (a;b), если f(x)= f(x);

2) т.Роля теряет силу, если хотя бы в одной (.) нарушаются условия дифференцированности;

3) в т.Роля нельзя заменить условия непрерывности на [a;b] на условия непрерывности на (a;b);

4) геометрический смысл т.Роля сводится к тому, что на графике ф-ии y=f(x) сущ.хотя бы одна (ξ , f(ξ)), в которой касательная параллельна оси Ox.

62. Теорема Коши.

Теорема Коши: если f(x)=y и g(x)=y непрерывны на [a;b], дифференцируемы на (a;b), при этом g’(x)≠0 для любого x, принадлежащему (a;b), то сущ. (.)ξ, принадлежащая (a;b), такая, что имеет место равенство:

=

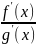
Док-во: g(b) и g(a)≠0, иначе по т. сущ. (.)ξ, принадлежащая (a;b)=g’(ξ)=0

Рассмотрим F(x)= f(x) - f(a) - * (g(x)-g(a)) в силу непрерывности f и g, F(x) непрерывна; F(x) дифференцируема на (a;b).

F(a) = f(a) – f(a) - * (g(a)-g(a)) = 0

F(b) = f(b) – f(b) - * (g(b)-g(a)) = 0 => F(a)=F(b)

тогда сущ. (.)ξ такая, что F’(ξ) = f’(ξ) - * g’(ξ)=0 => = .

Замечание: в т.Коши необязательно считать, что a<b.

63.Теорема Лагранжа.

Теорема Лагранжа: пусть y=f(x) непрерывна на [a;b] и дифференцируема на (a;b), тогда сущ. (.)ξ, принадлежащая (a;b) такая, что f(x)-f(a)=f’(ξ)*(b-a)

Док-во: пусть g(x)=x, тогда = => f(x)-f(a)=f’(ξ)*(b-a) ч.т.д.

64. Правило Лопиталя.

Теорема: если ф-ии f(x) и g(x) определены и дифференцируемы в окрестности (.)a=x (за исключением быть может самой (.)a) и f(x)= g(x)=0, где g(x) и g’(x)≠0 в этой окрестности, то имеет место формула: = [ ] = .

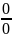Если сущ. , то сущ. .

Следствия:

1) = [ ] = =

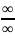2) f(x)*g(x)=[0; ] = =

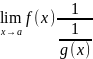3) [f(x)-g(x)] = [ ; ]= - ] = =

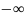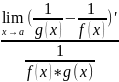
4) [f(x)]^g(x) = {[1^∞]; [0⁰]; [∞⁰]} = ^lnfg = ^glnf = g*limf) = [ ^0∞]

65. Формула Тейлора.

Теорема Тейлора: если y=f(x) определена в некоторой (.) x₀ и имеет в ней производные до (n+1)-порядка включительно, то для любого x из этой окрестности найдётся (.)ξ, принадлежащая (x; x₀), такая, что справедлива формула:

f(x) = f(x₀) + (x-x₀) + (x-x₀)² + (x-x₀)³ +…+ (x-x₀)ⁿ + Rn(ξ), где Rn(ξ) = 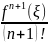(x-x₀)ⁿ⁺¹, а ξ=x₀+θ(x-x₀), где θ принадлежит (0;1).

Замечание: Rn (ξ) называется остаточным членом формулы Тейлора в форме Лагранжа. Иногда формула Тейлора записывается с остаточным членом в форме Пеано:

f(x)=f(x₀)+…+ (x-x₀)ⁿ + 0 (|x-x₀|ⁿ⁺¹), где 0 (|x-x₀|ⁿ⁺¹) – б/м ф-ия при х->x₀ (n+1)-порядка малости.

66. Достаточное условие монотонности.

Теорема: для того, чтобы дифференцируемая ф-ия f(x) была монотонно возрастающей (убывающей) на (a;b), достаточно, чтобы f’(x)>0 для любого x, принадлежащего (a;b).

Док-во: пусть f(x) возрастает на (a;b); докажем, что если f’(x)>0 => для любого x₁<x₂ => f(x₁) ≤ f(x₂), f(x₂) -f(x₁) = f’(ξ)(x₂-x₁), ξ принадлежит (x₁; x₂) => f(x₂)-f(x₁)>0 => f(x₁)<f(x₂) ч.т.д.

Замечание: если f(x) возрастает на [a;b] => f’(x) ≥ 0.

Интервалы, на которых ф-ия возрастает или убывает называются интервалами монотонности.

67. Первое достаточное условие экстремума.

Теорема: пусть f(x) непрерывна в окрестности (.)x₀ и дифференцируема во всех точках этой окрестности за исключением, быть может, самой (.)x₀. Тогда если f’(x) меняет знак с «+» на «-» при переходе через (.)x₀, то (.)x₀ – (.) локального min.

Критическими точками I рода называются точки, в которых f’(x)=0 или не существует.

68. Второе достаточное условие экстремума.

Теорема: если f’(x)=0, f’’(x₀)<0 , тогда (.)x₀ – (.) локального max., f’(x₀)=0, f’’(x₀), тогда (.)x₀ – (.) локального min.

Док-во: пусть f’(x)=0, f’’(x₀)<0.

f’’(x₀)= =

1 случай: ∆x>0, тогда <0 , т.к. ∆x>0, то f’(x₀+∆x)>0

2случай: ∆x<0, тогда >0 , т.к. ∆x<0, то f’(x₀+∆x)<0 =>(.)x₀ – точка локального min.

69. Асимптоты.

Асимптотой кривой y=f(x), имеющей ∞ ветвь, называется прямая ℓ такая, что расстояние от (.) x₀ до ℓ ->0.

Замечание: асимптоты делятся на: вертикальные, горизонтальные и наклонные.

Прямая x=a называется вертикальной асимптотой графика y=f(x), если хотя бы один из пределов f(x), f(x)=±∞

Замечание: вертикальные асимптоты располагаются в точках разрыва II рода.

Если y=f(x) задана при x->M (x<M), то прямая y=kx+b называется наклонной асимптотой, непрерывной кривой y=f(x) при x->±∞, если f(x)=kx+b+α(x), где α(x) – б/м при х->±∞.

70. Общая схема исследования функции.

1) Найти О.О.Ф.

2) Исследовать ф-ия в окрестности разрыва (найти вертикальные асимптоты).

3) Найти область значений функции.

4) Исследовать на чётность/нечётность.

5) Найти точки пересечения с осями координат:

с Оу: x=0 => y=…

c Ox: y=0 => x=…

6) Найти наклонные асимптоты.

7) Исследовать на монотонность extr.

8) Исследовать на выпуклость/вогнутость.

9) Нарисовать график.

71. Неопределённый интеграл. Основные определения и свойства первообразных.

Первообразной ф-ией для f=f(x) на [a;b] называется f=F(x), если она дифференцируема на этом промежутке, причём в точках a и b сущ. односторонние производные и F(x)=f(x) для любого x , принадлежащего (a;b).

Свойства первообразных:

1) Если F(x) первообразна для f(x) на [a;b], то F(x)+с, где с – произвольная постоянная, также является первообразной для этой ф-ии.

Док-во: (F(x)+c)’ = F’(x)+c=f(x)+0=f(x) ч.т.д.

2) Если F₁(x) и F₂(x) – две первообразные для ф-ии f(x), то их разность = const., где с – некоторая произвольная постоянная.

Док-во: φ(x) = F₁(x)-F₂(x)=c

φ’(x) = (F₁(x)-F₂(x))’=F’₁(x)-F’₂(x)=f(x)-f(x)=0

для любого х, принадлежащего [a;b] => φ(x)=c => F₁(x)-F₂(x)=c ч.т.д.

72. Неопределённый интеграл. Основные определения и геометрический смысл.

Первообразная является непрерывной кривой на [a;b].

Неопределённым интегралом f(x) называется семейство первообразных, т.е. выражение вида: F(x)+c.

Обозначения: ∫f(x)dx=F(x)+c, где х – переменная интегрирования, f(x) – подынтегральная ф-ия, f(x)dx – подынтегральное выражение.

Геометрический смысл неопределённого интеграла – семейство параллельных интегральных кривых.

73. Свойства неопределённого интеграла.

1) d(∫f(x)dx)=f(x)dx

Док-во: d(∫f(x)dx)=d(F(x)+c)=dF(x)+dc=F’(x)dx+c’dx=f(x)dx+0 ч.т.д.

2) dF(x)=F(x)+c

Док-во: dF(x)=∫F’(x)dx=∫F(x)dx=F(x)+c ч.т.д.

3) (∫f(x)dx)’=f(x)

Док-во: (∫f(x)dx)’=(F(x)+c)’=F’(x)+c’=f(x) ч.т.д.

4) ∫kf(x)dx=k∫f(x)dx, k-const.

Док-во: ∫kf(x)dx=∫kdF(x)= ∫dkF(x)=kF(x)+c=k∫f(x)dx ч.т.д.

5) ∫[f(x)+g(x)]dx=∫f(x)dx±∫g(x)dx.

74. Основные методы интегрирования. Метод замены переменной.

Теорема: пусть f(x) – непрерывная ф-ия x=φ(t) имеет непрерывную производную и f(φ(x)) имеет смысл, тогда справедлива формула: ∫f(x)dx=∫f(φ(t))* φ’(t)dt

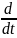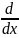Док-во: [∫f(x)dx]=f(x)*x'_t = [∫f(x)dx]* =f(x)*x’_t=f(φ(t))* φ’(t) – левая часть.

(∫(φ(t)* φ’(t)dt)=f(φ(t))* φ’(t) – правая часть.

75. Основные методы интегрирования. Метод заведения под знак дифференциала.

Замечание: если формулы интегрирования по частям прочитать справа налево, то получим метод введения под знак дифференциала.

76. Основные методы интегрирования. Метод интегрирования по частям.

Теорема: если ф-ия u=u(x), v=v(x) непрерывно дифференцируемы, то имеет место формула: ∫udv=uv-∫vdu

Док-во: d(u*v)=du*v+u*dv

∫d(u*v)= ∫(vdu+udv)= ∫v*du + ∫udv

u*v =∫vdu + ∫udv

∫udv=u*v - ∫vdu

C помощью интегрирования по частям берутся интегралы след. типов:

∫Pn(x) (= u) * ∫ {sinx/cosx/e^x/a^x} dx (=dv)

77. Интегрирование дробно-рациональных функций.

Теорема: всякая рациональная дробь представима и при том единственным образом в виде суммы многочленов и правильной рациональной дроби.

Метод разложения правильной рациональной дроби на сумму простейших дробей:

1) разложение знаменателя на простейшие множители:

Q_m(x)=(x-c₁)^k1*…*(x-c₂)^kℓ*(x₂+p₁x+q₁)^S1*…*(x₂+p_tx+q_t)^St+…+2S_t=m

c_{1 ,} c_2…p_1, q_1...p_t, q_t принадлежат R; k₁…k_ℓ, S₁…S_t принадлежат N.

2) выписать слагаемые в искомом разложении соответственно этим множителям:

(x-c)^k  + +…+

x-c 

(x²+px+q) 

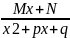
(x²+px+q)^k  + +…+ ,

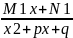3) тогда 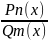будет представлена как сумма следующих простейших дробей:

+…+ +…+ +…+ + +…+ +…+ +…+ (1)

4) приводим правую часть выражения (1) к общему знаменателю и получим в числителе некоторый многочлен S(x) с неопределёнными коэффициентами:

5) сравнивая левые и правые числители, составить систему для определения неопределённых коэффициентов и решить систему:

6) подставляя найденные коэффициенты в разложение (1), получим искомые значения.

78. Интегрирование тригонометрических функций.

Теорема: если подынтегральная ф-ия есть рациональная ф-ия относительно sinx или cosx, то интеграл выражается через элементарные ф-ии путём подстановки.

t=tg (универсальная тригонометрическая подстановка) => sinx= , cosx= .

∫R(sinx,cosx)dx=∫R( ; )*

Частные случаи:

1)подынтегральная ф-ия нечётна относительно sinx:

R(cosx - sinx) - R(cosx , sinx) => делаем замену: t=cosx;

2)подынтегральная ф-ия нечётна относительно cosx:

R(- cosx , sinx) = - R(cosx , sinx) => делаем замену: t=sinx;

3)подынтегральная ф-ия чётна относительно sinx и cosx:

R(- cosx , - sinx) = R(cosx , sinx) => делаем замену: t=tgx;

4)подынтегральная ф-ия содержит только sinx и cosx чётных степеней:

∫sin^2k * cos^2ℓ x dx , (k, ℓ > 0) – в этом случае применяют формулу понижения степени;

5)интегралы вида:

а) ∫sinαx*cosβx dx = ∫[sin(α+β)_x + sin(α-β)_x ] dx;

б) ∫sinαx*sinβx dx = ∫[cos(α-β)_x - sin(α+β)_x ] dx;

в) ∫cosαx*cosβx dx = ∫[cos(α+β)_x + cos(α-β)_x ] dx.

79. Тригонометрические подстановки:

∫R(x)dx:

а) R, (x, ) , x = a sint , dx = a cost dt, x = a/t

б) R, (x, ) , x = a/cost, dx = (a sint)/(cos²t) dt

в) R, (x, ) , x = a tgt, dx = a/(cos²t) dt, x = a/t

80. Интегрирование некоторых иррациональных функций.

интегралы вида ∫ и ∫ dx вычисляются с помощью выделения полного квадрата под корнем.

81. Определение определённого интеграла. Его геометрический смысл.

Определённым интегралом y=f(x) на [a;b] называется предел интегральной суммы Sn = 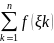*∆x_k (1) , если этот предел существует, конечен и не зависит от способа составления интегральной суммы.

= *∆x_{k ,} где a – нижний предел интеграла, а b – верхний.

Замечание:

1)определённый интеграл не зависит от того, какой буквой обозначено переменное интегрирование:

= =

2)если в качестве (.) ξ_k на [∆x_k-1] выберем (.), соответствующую наименьшему и наибольшему значению y=f(x) на этом промежутке, т.е. m_k ≤ f(ξ_k) ≤ M_k , то согласно суммы (1) получим: s= _k * ∆k , S= _k * ∆x_k , который называется соответственно нижней и верхней интегральной суммой или суммой Дарбу.

Геометрический смысл неопределённого интеграла:

Теорема 1 (усл. сущ. определённого интеграла): для того, чтобы существовал определённый интеграл, необходимо и достаточно, чтобы (S-s)>0, т.е. предел разности суммы Дарбу=0.

Теорема 2: если y=f(x) непрерывна или кусочно-непрерывна на [а;b], то она интегрируема.

Замечания:

1)ф-ия называется кусочно-непрерывной на промежутке, если имеет конечное число точек разрыва I рода;

2)среди разрывных ф-ий есть как интегрируемые, так и неинтегрируемые ф-ии.

82. Свойства неопределённого интеграла.

1) = -

2) 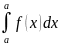= 0

3) = + - аддитивность по области

4) = α + β – линейность

Замечание:

4⁰) = k(b-a)

5) если f(x) ≥ 0 при любом x, принадлежащем [a;b] => ≥ 0

6) если f(x) ≤ g(x) при любом x, принадлежащем [a;b] => ≤

7) если f(x) принимает на [a;b] своё наименьшее и наибольшее значения, то f(x) ≤ M;

f(x) ≥ m => m(b-a) ≤ ≤ M(b-a)

8) | | ≤ |

9) Теорема о среднем: если y=f(x) непрерывна на [a;b], то на этом промежутке найдётся хотя бы одна (.)ξ, что справедливо равенство: = f(ξ)*(b-a)

10) = 0

Если подынтегральная ф-ия нечётная, то интеграл по симметричному промежутку = 0

11) = 2 , если f(-x)=f(x).

83. Теорема Барроу.

Теорема Барроу: производная интеграла с переменным верхним пределом = значению подынтегральной ф-ии на верхнем пределе.

( )’ = f(x)

Док-во: = φ(x), φ’(x) = f(x) , зададим приращение x -> ∆x, тогда ∆x – S криволинейной трапеции с основанием ∆x и высотой f(ξ), где ξ принадлежит [x; x+∆x].

∆φ = f(ξ) ∆x=> f(ξ)= ; перейдём к = φ’(x) = f(x) => φ(x) – первообразная для f(x).

84. Формула Ньютона-Лейбница.

Теорема Ньютона-Лейбница: если y=f(x) определена на [a;b] и имеет первообразную F(x) такую, что F’(x)=f(x), тогда = F(b)-F(a), т.е. определённый интеграл = приращению первообразной подынтегральной ф-ии на промежутке интегрирования.

Док-во: введём y=φ(x) = => φ(x), F(x) – первообразная для f(x)

φ(x) = F(x)+c ; докажем, что φ(b) = F(b) – F(a):

]x=a, φ(a) = = F(a)+c=0 => c = -(a), тогда φ(x) = F(x) – F(a)

]x=b, φ(b) = F(b) – F(a) ч.т.д.

85. Метод интегрирования по частям в определённых интегралах.

Теорема: пусть ф-ии u и v дифференцируемы на [a;b], тогда имеет место формула:

-

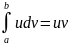Док-во: d(uv) = du*v + d => = +

= –

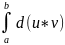= u*v -

86. Метод интегрирования заменой переменной в определённом интеграле.

Теорема: пусть дан , где f(x) непрерывна на отрезке ab.

Введём новую переменную x=φ(t), если:

1) φ(α) = а, φ(β) = b

2) φ(t) и φ’(t) – непрерывны на [α; β]

3) f(φ(t)) – определена и непрерывна на [α; β]

Тогда =

Док-во: см. док-во метода замены переменной в определённом интеграле;

∫f(x)dx = F(x) + c

∫f[φ(t)]* φ’(t)dt = F[φ(t)] + c => = F(b)-F(a)

= F[φ(β)] – F[φ(α)] = F(b) – F(a) ч.т.д.

87. Несобственные интегралы I рода.

Интегралы вида , , , где f(x) – определённая и непрерывная для всех х ф-ия, называются несобственными интегралами I рода или интегралами с бесконечными пределами.

Несобственный интеграл называется сходящимся (или сущ.), если сущ. конкретный предел определённого интеграла на [a;b] при стремлении какого-нибудь конца к бесконечности.

=

=

= + = +

Замечание: для того, чтобы сущ.последний интеграл, необходимо, чтобы оба предела были меньше бесконечности.

Несобственные интегралы I рода называются расходящимися, если предел от определённого интеграла = ∞ или не существует.

88. Несобственные интегралы II рода.

Пусть f(x) терпит разрыв II рода на [a;b].

Несобственные интегралы от ф-ий, терпящих бесконечный разрыв на каком-то конце интервала, либо в какой-то точке внутри интервала интегрирования, называются сходящимися, если существуют пределы от определённых интегралов вида:

= , x=a – разрыв II рода

= , x=b – разрыв II рода

= + = +

Замечания:

1) несобственные интегралы II рода называются интегралами от неограниченных ф-ий;

2) если (.) разрыва находится внутри интервала, то для того, чтобы интеграл сходился, необходимо, чтобы существовали и были конечны оба предела, стоящие с правой стороны;

3) если y=f(x) определена на [a;b] и имеет внутри этого промежутка конечное число (.) разрыва с₁, с₂…с_n, то интеграл от ф-ии представляется в виде:

= + +…+ .

89. Функция нескольких переменных. Основные определения.

Пусть D расположена в области Rⁿ . Если в каждой (.)М(x₁, x₂,…,x_n) принадлежит D в Rⁿ, по некоторому правилу подставить в соответствии с числом u=f(M), принадлежащим E в R¹, то говорят, что на множестве D задана ф-ия нескольких переменных или ф-ия (.).

1) M(x,y) принадлежит D в R²: z=f(x,y)=x²+y² – явно, а x²+y²+z²=1 - неявно

2) M(x,y,z) принадлежит D в R³: u=x+y*z-3 – ф-ия трёх переменных.

90. Предел и непрерывность ф.н.п. Свойства непрерывных функций.

Пусть y=f(M) определена в некоторой окрестности U(M₀) в Rⁿ за исключением, может быть, самой (.)M₀ , число a называется пределом ф-ии f(M) при M-> M₀ , если для любого E>0 сущ. δ>0 такая, что |f(M)-a|<E. =a, f(M) при M->M0  a.

Ф-ия f(M) непрерывна в (.)M0, если выполняются следующие условия:

1) f(M) определена в некоторой окрестность (.)M0;

2) сущ.предел при M->M₀ ф-ии f(M);

3) =f(M₀)

Ф-ия непрерывна в области, если она непрерывна в каждой (.) этой области.

Свойства ф-ий, непрерывных в области:

1)если f(M) и g(M) непрерывны в некоторой окрестности (.)M₀ , то их сумма, разность, произведение и частное при условии, что g(M₀)≠0, также непрерывна в U(M₀);

2) если f(M) непрерывна в (.)M₀ и f(M₀)≠0, то сущ. δ>0 для любого E_uδ(M₀) => f(M)≠0 и имеет тот же знак, что и f(M₀);

3) если f(M) непрерывна в ограниченной и замкнутой области , то она ограничена в этой области, т.е. сущ. N>0 такая, что для каждой M, принадлежащей => |f(M)|≤0;

4) если f(M) непрерывна в ограниченной и замкнутой области , то она принимает в своё наибольшее и наименьшее значения, т.е. сущ. (.)M₁, M₂ , принадлежащие : f(M₁) -> min, f(M₂) ->max;

5) если f(M) непрерывна в ограниченной и замкнутой области и сущ. (.)M₁, M₂ , принадлежащие , в которой ф-ия имеет разные знаки, то сущ. (.)M₀ из такая, что f(M₀)=0.

Множество точек, в которых нарушается условие непрерывности ф-ии, называется множеством точек разрыва ф-ии.

91.Частные производные I порядка ф.н.п.

Частным приращением f(x) в (.)M по переменной x_k с шагом ∆x_k называется величина ∆x_kf = f(M₁)-f(M)=f(x₁, x₂,…,x_k+∆x_k,…,x_n) – f(x₁, x₂,…,x_k+∆x_k,…,x_n).

Частной производной f(x) по переменной x_k называется предел отношения частного приращения ф-ии f(x) по x_k к приращению аргумента ∆x_k при стремлении последнего к нулю произвольным образом.

f’_xk(M) = (M) =

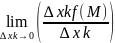
Замечания:

1) частная производная существует, если существует предел, стоящий в правой части равенства;

2) вычисление частной производной сводится к вычислению обычной производной от f(x), если переменные (x₁, x₂,…,x_k-1 , x_k+1,…,x_n) считать const.

Частный случай: z=f(x,y), тогда _∆xz = f(x+∆x,y) – f(x,y)

_∆yz = f (x,y+∆y) - f(x,y)

z’_x = =

z’_y = =

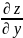92. Частные производные высших порядков ф.н.п.

Частной производной «n»-порядка называется производная по какой-либо переменной от некоторой частной производной n^-1 – порядка. = [ ]

Замечание: если при дифференцировании используется , то такие производные называются смешанными.

Теорема: пусть f=z(y) определена вместе со своими частными производными в (.)M₀ (x₀,y₀) причём и тогда =

Замечание: теорем верна и для производных старших порядков.

93. Полный дифференциал ф.н.п. I порядка.

Полным приращением в (.)M называется выражение вида ∆f(M)-f(M1)-f(M)=f(x₁₊∆x₁, x₂ + ∆x₂,…,x_k + ∆x_k ,…, x_n+∆x_n)

Дифференциалом I порядка y=f(M) называется выражение вида dt(M) = 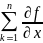(M)dx_k = f’x₁dx₁+f’x₂dx₂+…+f’x_kdx_k+…+f’x_ndx_n

Частные случаи:

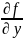n=2 : z=f(x,y) , dz = dx + dy

n=3 : u=f(x,y,z) du = dx + dy + dz

94. Производная по направлению.

Пусть в области Ω в R³ ; u = f(x,y,z) и вектор ℓ = { ℓ_x , ℓ_y , ℓ_z }.

Производной от ф-ии f(x,y,z) в (.)M₀ (x,y,z) в направлении вектора ℓ называется предел отношения при ∆ℓ -> 0, где ∆ℓ = |вектор ∆ℓ|=

= , = *cosα + *cosβ + *cosγ

95. Градиент ф.н.п. и его свойства.

Градиентом ф-ии называется вектор, проекция которого на оси координат равны частным производным этой ф-ии по соответствующей координате. f = grad f = [ … ]

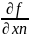Частный случай: z=f(x,y) , z = {f’_x ; f’_y} , u = f(x,y,z), u = {u’_x;u’_y;u’_z}

Замечание: градиент z=f(x,y), который задаёт поверхность в пространстве R³ , является вектором, направленным по нормали (перпендикулярно) к данной точке.

Свойства градиента:

1) Производная по направлению вектора ℓ = скалярному произведению градиента ф-ии на орт этого направления (орт – вектор единичной длины, имеющей то же направление, что и исходящий вектор).

Следствие: производная по направлению = проекции градиента на это направление.

2) Производная по направлению принимает своё наибольшее значение, если это направление совпадает с градиентом этой ф-ии. max = || f||

Док-во: = || f||*||вектор ℓ⁰||*cosφ = || f||*cosφ, max cosφ=1, φ=0 => вектор ℓ= f.

3) Градиент ф-ии f(m) направлен по нормали к поверхности уровня в сторону возрастания ф-ии.

4) Производная по направлению вектора, касательного к поверхности уровня, равна 0.

96. Дифференциалы высших порядков ф.н.п.

d²f = )² f*dx_i*dx_j

Частные случаи: n=2 , d²f )² f*dx*dy = dx² +2 dxdy + dy²

97. Дифференцирование сложных ф.н.п.

98. Дифференцирование неявно заданных ф.н.п.

99. Интеграл по области. Определение.

Интегралом от ф-ии f(M) по области Ω в Rⁿ называется предел интегральной суммы (1) при стремлении к 0, если этот предел существует, конечен и не зависит от способа составления интегральной суммы.

∫f(M)dμ = _i)*∆μ_i

Диаметром области D называется max из расстояний между любыми двумя точками этой области.

100. Интеграл по области. Свойства.

1)

2) = _{1 2} тогда = +

3) = k

4) = +

5) если f(M) ≥ 0 для любой M, принадлежащей Ω, то ≥ 0

6) если f(M) ≤ для любой M, принадлежащей Ω, то ≤

7) если m ≤ f(M) ≤ для любой M, принадлежащей Ω, то m* (Ω) ≤ ≥ (Ω)

8) | | ≤

101. Двойной инт-л. Рассмотрим плоскую обл-ть D и ф-цию f(x,y)-непрерыв в D. 1.разобъем обл-ть произвольным образом на n-непересек частей. D=U_i=1ⁿD_i, 2. в каждой подобласти D_i произв образом выберем (·) M_i (x_i,y_i), 3.i=1,n. f(M_i)=f(x_i,y_i) и f(M_i)·∆s_i, 4.λ=max обознач через λ max из диаметр частич областей. 5. Составим "n"-ую интегр сумму S_n=∑f(M_i) ·∆s_i=∑f(x_i,y_i) ·∆s_i.(1) Перейдем к графику в интегр сумме (1)при λ ,т.е. при стягив max из частич областей в точку. Двойным инт-лом по обл назыв lim инт-ой суммы (1) при λ , если этот lim сущ,конечен и не зависит от способа составления инт суммы . = . Геом смысл:а)если подинтегр ф-ция =1,то =S(D)-площадь обл-ти.б)если f(x,y)≥0,то =V цилиндр поверх

102. Вычисление двойного интеграла в декартовой системе координат. а)рассмотрим обл-ть:D-прямоуг, задаваемый неравенство м, D_i-прямоуг со сторонами ∆x_i и ∆y_j ⇒∆s_ij=∆x_i·∆y_j; S_n=∑f(M_i) ·∆s_i=∑f(x_i,y_j) ·∆s= ∑f(M_k) ·∆s_k=∑_i=1∑_j=1f(x_i,y_j)·∆x_i·∆y_j; введем: λ₁=max ∆x_i 0, λ₂=max ∆y_j 0 поэтому = =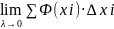 = Вывод: для того чтобы высчитать двойн инт-л по прямоуг надо подинт ф-ию f(x,y) проинт сначала по перемен y от нижнего предела с до верхнего d считая их с константой, а затем получен ф-цию проинт в промеж (a,b) Рисунок

Пример: , D= , = = = dx=26/3 =26/3 =13/3.

Обл-ть назыв правильной в направл иси oy,если:1.проекция обл на ось ox=промеж(a,b);2.любая прямая,провед внутри этой обл || оси oy пересек границу этой обл не боле чем в 2х точках, т.е. обл задается D= Рисунок

Обл-ть назыв правильной если она правильная в направлении обеих осей.

103. Криволин коорд-ты. Пусть на плоск R²(oxy) задана обл-ть D, опред-мая сист нерав (1),рассмотр R² с введён на ней сист корд (oξη).Тогда сист (1) каждой (·)М(x,y) из D поставит в соотв (·)N(ξ,η) из D^~. Если т.М будет перемещ внутри обл D,то в то же время тN будет перемещ в обл D^~⇒D D^~. Если двум различн тМ будут соотв две различ тN то можно утверждать,что сист(1) будет разрешима однознач относительно x,y, т.е. можно рассматр сист: 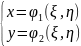(2) при этом D^~ D. При этом между обл D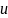^~ D возникает взаимно однозначное соотв и набору корд тМ(x,y) будет соотв единств набор корд (ξ,η) ⇒ корд (ξ,η) можно рассматр как коорд тМ. Рисунок

Линии,на кот одна из корд принимает постоян знач назыв координ линиями.В R² (x,y) это:x=x₀,y=y₀, в R²(ξ,η) это: ξ= ξ₀, η= η₀.

104. Элемент площади в криволин коорд. Рассмотр , R²(oξη) R²(oxy) Рисунок

Рассмотр R²(oξη) ∆s; A₁=(ξ,η)=B₁(x,y)=B₁(x(ξ,η),y(ξ,η)), A₂=(ξ+∆ξ,η)= B₂(x(ξ+∆ξ,η,η),y(ξ+∆ξ,η)), A₃=(ξ+∆ξ,η+∆η)= B₃(x(ξ+∆ξ,η+∆η),y(ξ+∆ξ,η+∆η)), A₄=(ξ,η+∆η)= B₄(x(ξ,η+∆η),y(ξ,η+∆η)). ∆s^~=∆ξ·∆η. J(ξ,η)= -якобиан, сл-но: ∆s^~= |J(ξ,η)|·∆ξ·∆η –геом.смысл якобиана заключ в том,что он=коэф искажен площади.

105. Замена перемен в двойн инт-ле. для того чтобы сделать замену необход:1.в f(x,y)вместо x и y подставить x(ξ,η) и y(ξ,η),2.dxdy заменить на |J(ξ,η)|dξdη,3.заменить обл D на D^~. = . Пример: ,где D=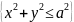 , x=rcosφ,y=xsinφ, f(r,φ)= = ; D^~= ⇒ I= =-1/2 =1/3a² =2πa²/3

106. Тройной инт-л от ф-ции f(x,y,z) по обл Ω – lim инт-ой суммы: ∑f(x_i,y_i,x_i)·∆v_i при λ ,где λ-max из диаметров частич областей (т.е.при стягив частич обл в (·) если этот lim сущ,конечен и не зависит от способа составления интегр суммы): 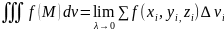. Замеч: если обл-ть Ω разбивать на частичн обл-ти плоскостями ||координ плос-ям,то в кач-ве частичн обл-ей получ элементар параллелепипед,Vкоторого=∆x·∆y·∆z.Геом смысл:исходя из св-в инт-ла по обл-ти,если f(x,y,z)=1 ⇒ = V(Ω)

107. Вычисл тройного инт-ла в декарт координ. Пусть некот простран обл Ω ограничена замкн пов-ю Q=Fr Ω. Простр обл Ω назыв правильной в направлении оси oz,если:1.любая прямая || оси oz пересек поверхн Q не более,чем в 2-х (·),2.вся обл Ω проектир на плоск oxy в правильную плоскую обл-ть D. Простр обл Ω назыв правильной если она правильна в направ всех 3-х осей. Замеч:если обл Ω правильная,то она задаётся след сист двойн неравенств: Ω=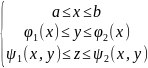 (1), где φ₁(x), φ₂(x)-верх и ниж границы плоской обл-ти D, ψ₁(x,y), ψ₂(x,y)- верх и ниж пов-ти огранич-е Ω. Рисунок

Если простр обл Ω задается сист нерав (1),то 3-ой инт-л ф-ции = .Вывод:чтобы вычислить 3-ой инт-л в дек.коорд надо обл-ть Ω представ в виде нерав (1) и проинт ф-цию f при произв,но фиксир x,y, т.е. считая их const в пределах от (·) входа на нижн пов-ти ψ₁(x,y) до (·) выхода на верх пов-ти ψ₂(x,y). Затем,получ рез-т проинт при произв,но фиксир x от ниж границы φ₁(x) до верх φ₂(x) обл-ти D. Проинт получ рез-т по х в пределах его наиб изменения в обл-ти D.

108. Вычисление 3-го инт-ла в криволин коорд. Пусть (2). Определ взаимнооднознач соотв обл-ти Ω из пр-ва oxyz и обл-ти Ω^~ в пр-ве O'_ξ,η,χ, тогда М(x,y,z) Ω ! (·)M^~( ) Ω^~. Таким образом набор можно рассматр как корд тМ,кот будут являться криволин корд в простр Oxyz. Аналогич рассужд для 2-х мерной обл можно записать,что ∆V=|J( )|∆V^~+O(∆V^~), где ∆V-объем эл-та тела в Oxyz, ∆V^~-\\в O .Модуль якобиана=коэф искаж объема при соотв преобразовании λ=diam(λ_i^~),где λ_i^~ =V(λ_i^~)-диам частич тела. Замена перемен:1.заменить коорд ф-ции по формулам(2)=f(x( )) и тд.,2.эл-т Vdv=dxdydz=|J( )|dξdηdχ,3.обл-ть Ω заменить на обл Ω^~.

109. Числ рядом наз выражение вида a₁+a₂+…+a_n=∑a_n(1), где а₁,а₂-члены ряда,а_n-общий член ряда.Замеч: для того,чтобы задать ряд достаточно записать правило определ общего члена а_n. Сумма первых n-членов ряда наз n-ой частич суммой, Sn=a₁+a₂+…+a_n. Суммой ряда (1)наз конеч или бесконеч lim частич суммы Sn при n ∞: S=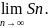 Числ ряз наз сходящимся,если его сумма конечна и расходящ,если его сумма=∞ или не сущ.

110.Свойства сходящ рядов. Т-ма1:если члены сход р - a₁+a₂+…+a_n=∑a_n ,имеющего сумму S умнож на число λ≠0 то получ ряд ∑(λа_n) так же будет сход-ся,при этом его S^~=Sλ.Док-во1: S= , S^~=λa₁+λa₂+λa_n=λ(a₁+a₂+…+a_n)=λSn. ^~= =λ =λS. Т-ма2: пусть ∑a_n-сход и имеет своей суммой число А, ∑b_n-сход,В. Тогда эти два ряда можно склад(вычит) так,что ряд ∑a_n±b_n сх-ся и его сумма=А±В. Док-во2:Sn^~=(a₁±b₁) +( a₂±b₂)+( a_n±b_n)=Аn±Вn. Т-ма3: ряд-a₁+a₂+…+a_n и его остаток (ряд a_n+1+a_n+2+…+a_n-р получ из р(1) отбрас перв n-членов наз n-ым остатком р(1)) сход-ся или расх-ся одноврем.Док-во3:состав n-ую частич сумму р(1):Sn= a₁+a₂+…+a_n=S_k+S^~_n-k.Sk-частич сумма р1, S^~_n-k-частич сумма р 3. = , таким образом на сход част суммы и сход р1 влияет сход частич р3 и наоборот ⇒если сущ ⇒сущ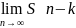 . Т-ма4:если р1 сход-ся,то lim его n-го остатка при 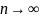=0. Док-во4:∑_k=n+1a_k=R_n,тогда R_n=S-S_n, Rn= S-Sn=S- =S-S=0

111. Необход признак сход-ти рядов. Т-ма:если р a₁+a₂+…+a_n=∑a_n сход-ся,то его общ член a_n стремится к 0 при n ,т.е. ,=0. Док-во:Sn= a₁+a₂+…+a_n-1+a_n. S_n-1= a₁+a₂+…+a_n-1. Тогда можно заметить,что n-ый член представл собой разность a_n=S_n-S_n-1. = = - Sn-1=S-S=0. Следст:достаточ призн расходим р:если общ член р не стремится к 0 при n _{,то р расх=ся.}Пример:∑n²/(5n²+3n), a_n= n²/(5n²+3n) n n²/5n²=1/5≠0-р расх-ся.

112. Признаки сравнения рядов с положительными членами. Ряд a₁+a₂+…+a_n=∑a_n назыв р с положит членами,если для любого n a_n≥0. Т-ма1:признак сравн1: пусть ∑ a₁+a₂+…+a_n (1)и ∑ b₁+b₂+…+b_n (2)если каждый член р(1) не превосх соотв члена р(2),т.е. a_n≤b_n то:а)из сходим р с больш членами(2) следует сход-ть р с меньш членами(1),б)из расх-ти р с меньш членами(1) след расх-ть р с больш членами(2). Т-ма2:признак сравн2:если сущ конеч и отлич от 0 =k (≠0,<∞) то р(1)и(2) сход-ся и расх-ся одновремен. Следст:если общ члены сравнив рядов эквивал при n _, то оба ряда ведут себя одинаково. Замеч:сравнение исслед р проводится со след эталон р:∑1/n^p-обобщ гармон р (р Дирихле) про кот известно,что если p>1-р сх-ся, p≤1-р расх-ся;∑1/n-гарм р,расх т.к. p=1

113. Достат признаки сход р с полож членами.а)признак Даламбера:(использ при a_n=n!,/ и· n^p,aⁿ).Т-ма:если в р с положит членами ∑а_n(a_n≥0)(1) отношение (n+1)-члена к n-му члену при имеет конеч lim d (lima_n+1/a_n=d), то р сход-ся если d<1, р расх-ся если d>1.Замеч:если d=∞ р расх-ся,если d=1 треб доп исслед,т.е. применить другой признак.б)радикал признак Коши:Т-ма:если для р с положит членами величина при имеет конеч lim –d (lim =d),то если d<1-р сх-ся,если d>1-р расх-ся.Замеч:1)такое же,2)этот признак удобно применять в тех случ,если общий член р явл степенью какого-нить выражения.в)интегр признак Коши:Т-ма:пусть общ член р с положит членами (1) а_n=f_n.Если ф-ция f(x),принимающая в (·)х=n хнач f(n),монотон убывает на промеж (1,∞) то р(1) и несобств инт-л сход или расх одновремен.Замеч:1)чтобы получить ф-цию f(x) надо в общем члене заменить перемен n на х.2)этот признак удобно применять в тех случ,когда выраж а_n легко инт-ся,в частности методом завед под знак диф-ла.

114. Знакочеред р наз р вида а₁-а₂+а₃-а_n+…+(-1)ⁿ⁺¹a_n=∑(-1)ⁿ⁺¹a_n+1,где a_n+1>0 (1). Признак Лейбница: если в знакочеред р(2) начин с некотор места члены р по абсолют величине монотон убыв-ие и общ член стремится к 0,тоеть 1.lima_n=0,2.a_n>a_n+1 то р сх-ся,его сумма положит и непревосх абсолют велич 1-го члена,т.е. S≤a₁. Док-во:S_2m=(а₁-а₂)+(а₃-а₄)+(а_2m-1-a_2m)>0, S_2m=а₁-(а₂-а₃)-(а₄-a₅)-…-(а_2m-1-a_2n)-a_2m⇒S_2m<a₁, S= lima_n+1S_2m⇒0<S<a₁, S_2m+1= S_2m+a_2n+1, S=lim(S_2m+a_2m)=lim S_2m+lim a_2m=S+0=S Объед рассужд для S_{2m и} S_2m+1 ⇒0<S<a₁

115. Р вида а₁+а₂+а₃+а_n+…=∑a_n(1) где a_n-общ член р может принимать как полож так и отриц знач наз знакоперемен. Достат призн сход знакоперем р:Т-ма:если р |а₁|+|а₂|+|а₃|+|а_n|+…=∑|a_n|(2) составл из абсолют величин,членов р(1), сход-ся то и р(2)сх-ся,при этом говорят,что р(1) сход абсолютно. Пример:∑sinnα/n², ∑|sinnα/n²|=∑|sinnα|/n²≤∑1/n²(p=2>1⇒р сход-ся⇒∑|sinnα|/n²-сх-ся⇒∑sinnα/n²-сх-ся абсолютно.Замеч:знакочеред р явл-ся частн случаем знакоперемен р,поэтому его исслед провод в два этапа:1.-абсолют сх-ть исслед,если её нет переходят ко 2 этапу-исслед сх-ти по Лейбницу,сход по Лейбн наз условная сход.Пример:∑(-1)ⁿ⁺¹/n, 1этап(абсолют сх-ть): ∑|(-1)ⁿ⁺¹/n|=∑1/n-гармонич р,т.к.р=1-р рас-ся⇒абсолют сход-ти нет,2 этап(услов сх-ть): ∑(-1)ⁿ⁺¹/n-сх-ся(см призн Лейбница)

116. Р вида u₁(x)+u₂(x)+u₃(x)+…+u_n(x)=∑u_n(x) (1) где u_n(x) –некотор ф-ция наз функцион рядом. Замеч:если аргумент х приним конкрет знач x₀,то функцион р становится числовым рядом ∑u_n(x₀) (2) и может бытьисследован с помощью признаков сход-ти числ рядов. Если р(2) сх-ся,то (·)х₀ наз (·)сх-ти для р(1);если р(2) рас-ся,то (·)х₀ наз (·)расх-ти. Множество всех знач х,для кот функцион р(1) сх-ся наз обл-ю сход-ти этого р. N-ой частич суммой р(1) наз выражение вида S_n(x)= u₁(x)+u₂(x)+u₃(x)+…+u_n(x); R_n(x)= u_n+1(x)+u_n+2(x)+ …=∑_k=n+1u_k(x) наз n-ым остатком р(1). Если функц р имеет нанекотор множ-ве своей суммы ф-цию S(x),то говорят,что функцион р сх-ся на этом множ-ве к ф-ции S(x):S(x)=limS_n(x). Степен р наз функцион р вида ∑c_n(x-a)ⁿ,где c_n-коэф р, а R.

117. Т-ма Абеля. Замеч:y=x-a,то получ р ∑с_nyⁿ(3) кот также явл степен р,но прост при изуч. Т-ма Абеля:1)если степен р ∑с_nхⁿ-сх-ся при x=x₀≠0,то он абсолютно сх-ся для всех x:|x|<|x₀| Рис 2)если р рас-ся при х=х₁≠0,то он расх-ся х: |x|>|x₀| Рис. Следств:для степен р(3) сущ симметрич относит нач коорд интервал –R<y<R,для всех (·)кот,степен р сход-ся абсолютно,а для |y|>R-р расх-ся.

118. Св-ва степ р: инт-л сходим степен р-инт-л (-R;R)такой,что для всех y,лежащ внутри инт-ла р сх-ся,а для всех y,лежащ вне инт-ла р расх-ся. Радиус сх-ти R степен р-число=половине длины инт-ла сход-ти с центром в нач коорд. Замеч: Рис 1)если степен р сх-ся только при х=0,то счит R=0;если р сх-ся всюду,то R=∞.2)т.к. т-ма Абеля не дает ответа на вопрос о сх-ти на концах инт-ла сх-ти,то исслед-ния в (·)х=R и х=-R провод для каждого конкрет р с использ признак сход-ти числ р отдельно.

119.Р Тейлора и Маклорена. Пусть ф-ция f(x) задана на некот инт-ле,содерж (·)А и бесконеч диф-ма в окрестности этой (·).Тогда степен р вида ∑(f⁽ⁿ⁾(a)/n!)(x-a)ⁿ(1) наз р Тейлора ф-ции f(x)и записыв f(x)~ ∑(f⁽ⁿ⁾(a)/n!)(x-a)ⁿ. Замеч:к бесконеч диф-мым ф-ям относятся степен,тригоном и остальные элемент ф-ции. Если р Тейлора сх-ся на инт-ле зад ф-ции f(x) и в каждой (·)этого инт-ла его сумма=соответ знач ф-ции,то имеет место рав-во: f(x)= ∑(f⁽ⁿ⁾(a)/n!)(x-a)ⁿ,кот наз разлож ф-ции в р Тейлора. Замеч:р Тейлора явл степен,при этом коэф разлож вычисл по ф-ле c_n=f⁽ⁿ⁾(a)/n!. Частн случай р Тейлора соотв-ий знач a=0 наз р Маклорена: ∑(f⁽ⁿ⁾(0)/n!)(x)ⁿ.

120. Степенные ряды применяются в приближенных вычислениях: для вычисления ф-ций, определ интегралов, численного интегрир диф-ных уравнений и т. п. При этом полезно знать разложение в степенной ряд Тейлора некоторых функций; в скобках указан интервал сходимости ряда.

1. 2.

3. 4.

5. 6.

Пример. Вычислить с точностью до 0,0001 , разложив подынтегральную функцию в ряд и затем проинтегрировав почленно. Воспользуемся разложением функции , положив .

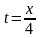Получили знакочередующийся ряд Лейбница. Для оценки остатка ряда используем признак Лейбница: . При вычислении интеграла необходимо обеспечить точность 0,0001, т. е. , следовательно, начиная с четвертого члена (0,00002), можно все члены ряда отбросить, вычисления ведем с одним запасным знаком, округляем до 0,0001: .

121. Локальный экстремум ф.н.п. (·)М₀(x₀,y₀) наз лок min(max) ф-ции z=f(x,y),если (·)М(x,y) U(M₀)⇒f(x₀,y₀)≤f(x,y)( f(x₀,y₀)≥f(x,y)). (·)лок extr наз (·) лок min(max). Т-ма1(необход услов лок extr):для того,чтобы ф-ция z=f(x,y) имела в (·)М₀(x₀,y₀) лок extr необход,чтобы в этой (·) она была 2-диф-ма и её частные произв 1-го порядка= в этой(·) 0. (·) в которых частн произв 1-го порядка обращ в 0 наз стационарными (·) этой ф-ции. Т-ма2(достат услов лок extr ф-ции 2-х перемен):пусть ф-ция z=f(x,y) 2-ды диф-ма в окрест (·)М₀(x₀,y₀) и имеет в этой(·) нулевые частные произв 1-го порядка. Обознач через А=z_xx''(x₀,y₀),B= z_xy''(x₀,y₀),C= z_yy''(x₀,y₀) и через ∆:определитель . Тогда (·)М₀(x₀,y₀) будет явл (·) лок extr,если ∆>0 при этом:если А<0,то(·)М₀-(·)лок max, если А>0,то(·)М₀-(·)лок min.Если же ∆<0, то в (·)М₀-лок extr нет,а при ∆=0 необход провести доп исслед.Пример:z=x²+y² 1.найти стац(·) ⇒ М₀(0,0)-cтац(·). А= z_xx''=2, B= z_xy''=2, C= z_yy''=2. ∆= =4>0⇒сущ extr т.к. А>0⇒(0,0)-лок min.

122. Условный экстремум ф.н.п. Пусть ф-ция z=f(x,y) определена в некот обл-ти D изR² и в этой же обл-ти задана кривая уравнением φ(x,y)=0(ур связи). Услов extr ф-ции 2-х перемен z=f(x,y) наз её extr при условии,что (·) берутся на задан кривой.Для нахожд условн extr использ 2 метода:1)мет подстановки-если из уравнения связи можно ярко выделить y=y(x) то задача о нахожд усл extr сводится к задаче о нахожд extr ф-ции одной перемен,2)мет множителей Лагранжа-вопрос о существ и хар-ке условн extr решается на основании изучения знака диф-ла 2-го порядка ф-ции Лагранжа: d²F=F_xx''dx²+2F_xy''dxdy+F_yy''dy² при условии,что диф-л уравнения связи=0:4x'dx+4y'dy=0 tckb d²F<0-min,если d²F>0-max.