
- •Аннотация
- •Методические указания для студентов
- •Глава 1. Уравнение прямой и кривые второго порядка на плоскости
- •Блок самопроверки:
- •Список литературы:
- •Глава 2. Понятие вектора и операции над векторами
- •Блок самопроверки:
- •Список литературы:
- •Глава 3. Уравнения прямой и плоскости, поверхности второго порядка в пространстве
- •Блок самопроверки:
- •Список литературы:
- •Глава 4. Матрицы и операции над ними. Определитель и ранг матрицы, их свойства
- •Блок самопроверки:
- •Список литературы:
- •Глава 5. Системы линейных уравнений, способы их решения
- •Блок самопроверки:
- •Список литературы:
- •Глава 6. Теория пределов, непрерывные функции, разрывы
- •Часть 1. Пусть ограниченны сверху, т.Е. Такое, что . Тогда, согласно теореме о существовании супремума мы можем утверждать, что .
- •Часть 2. Пусть теперь неограниченна сверху. Это значит, что .
- •Блок самопроверки:
- •Список литературы:
- •Глава 7. Производная, порядок и свойства производной, исследование функций
- •Блок самопроверки
- •Список литературы
- •Глава 8. Интеграл, его свойства, вычисление площадей и объемов фигур
- •Блок самопроверки
- •Список литературы
- •Глава 9. Ряды, виды рядов, сходимость рядов
- •Блок самопроверки
- •Список литературы
- •Глава 10. Дифференциальные уравнения, их виды и решение
- •Блок самопроверки
- •Список литературы
- •Глава 11. Комбинаторика. События, действия с ними, вероятность, виды, основные теоремы и формулы
- •Блок самопроверки
- •Список литературы
- •Глава 12. Случайные величины, их виды, законы и функции распределения. Закон больших чисел
- •Блок самопроверки
- •Список литературы
- •Глава 13. Математические модели видов и процессов в системе социальной работы
- •Блок самопроверки
- •Список литературы
- •Глава 14. Математические методы исследования в социальной работе
- •Блок самопроверки
- •Список литературы
- •Глоссарий
Блок самопроверки:
Пример 1.
Пределы не содержащие неопределенности:
![]() ,
аналогично решаются остальные примеры
,
аналогично решаются остальные примеры
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Пределы
с неопределенностью вида
![]()
Пример 2.
![]() Разделим
числитель и знаменатель на
Разделим
числитель и знаменатель на
![]()
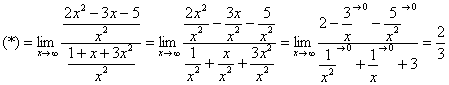
Пример 3.
![]() Разделим
числитель и знаменатель на
Разделим
числитель и знаменатель на
![]()
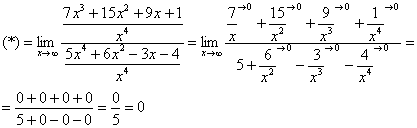
Пример 4.
![]() Разделим
числитель и знаменатель на
Разделим
числитель и знаменатель на
![]()
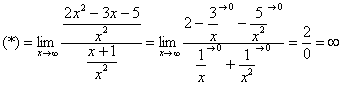
Пределы
с неопределенностью вида
![]()
Пример 5.
![]()
Разложим числитель на множители.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 6.
![]()
Разложим числитель и знаменатель на множители.
Числитель:
![]()
Знаменатель:
![]()
![]()
![]()
![]() ,
,
![]()
![]()
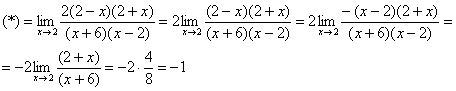
Пример 7.
![]()
Умножим числитель и знаменатель на сопряженное выражение.
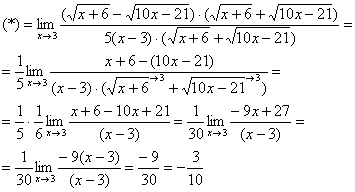
Пример 8.
![]()
Разложим числитель на множители:
![]()
![]()
![]()
![]()
![]()
![]()
Умножим числитель и знаменатель на сопряженное выражение

Список литературы:
Балдин, К.В. Краткий курс высшей математики / К.В.Балдин, Ф.К.Балдин, В.И.Джеффаль – М.: Дашков и Ко, 2009 (электронный ресурс «Университетская библиотека»);
Малыхин, В.И. Высшая математика: Учебное пособие / В.И.Малыхин – М.: Инфра-М, 2009 (электронный ресурс «Университетская библиотека»);
Самарин, Ю.П. Высшая математика / Ю.П.Самарин, Г.А.Сахабиева, В.А.Сахабиев – М.: Машиностроение, 2006 (электронный ресурс «Университетская библиотека»).
Глава 7. Производная, порядок и свойства производной, исследование функций
Определение и геометрический смысл производной
Пусть
функция
f(x) непрерывна
в точке
![]() .
.
Определение.
Производной от функции
![]() в
точке
называется
величина
в
точке
называется
величина
![]()
Дадим некоторые расшифровки этого важнейшего понятия математического анализа.
а)
Вспоминая определение предела можно
записать определение
![]() через
кванторы .
через
кванторы .
б)
Величина
![]() называется
приращением аргумента, а величина
называется
приращением аргумента, а величина
![]() приращением
функции. Тогда
приращением
функции. Тогда
в)
Обозначая
![]() ,
можно записать
,
можно записать
![]()
Понятие
производной впервые появилось в физике
в связи с понятием скорости. Пусть
некоторая материальная точка движется
по оси
![]() так
что
так
что
![]() есть
координата точки в момент времени
есть
координата точки в момент времени![]() .
Спустя время dt координата точки будет
.
Спустя время dt координата точки будет
![]() ,
т.е. за время
,
т.е. за время
![]() точка
пройдет путь
точка
пройдет путь
![]() .
Поэтому средняя скорость точки за
интервал времени
будет
равна
.
Поэтому средняя скорость точки за
интервал времени
будет
равна![]() .
Чтобы найти мгновенную скорость точки
в момент времени
надо
устремить
кнулю, т.е.
.
Чтобы найти мгновенную скорость точки
в момент времени
надо
устремить
кнулю, т.е.
![]()
Таким
образом, производная от координаты
точки определяет ее мгновенную скорость.
Поэтому и производную функции
![]() в
некоторой точке
можно
трактовать как скорость изменения
функции.
в
некоторой точке
можно
трактовать как скорость изменения
функции.
Дадим
еще геометрический смысл производной.
В определение производной входят две
операции: деление
![]() и
предельный переход при
и
предельный переход при
![]() .
Что же это дает?
.
Что же это дает?
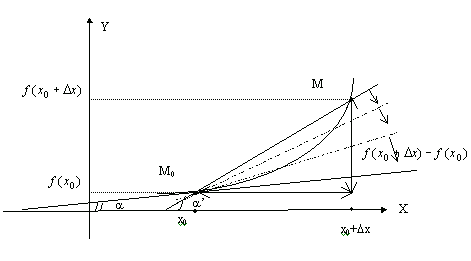
Нанося
на график точки с координатами (![]() ,
,
![]() )
и (
)
и (![]() ,
,
![]() )
мы получим фигуру изображенную на
рисунке. Проведем через эти точки линию,
которая называется секущей. Тогда дробь
есть
не что иное как
)
мы получим фигуру изображенную на
рисунке. Проведем через эти точки линию,
которая называется секущей. Тогда дробь
есть
не что иное как
![]() ,
где
,
где
![]() есть
угол наклона секущей к оси OX.
есть
угол наклона секущей к оси OX.
Но,
в определении производной есть еще
предельный переход при
![]() .
Что же дает этот предельный переход?.
.
Что же дает этот предельный переход?.
При
точка
M начинает двигаться к точке M0.
При этом вся секущая будет поворачиваться
около точки M0
и в пределе она превратиться в касательную
к точке M0.
Угол
при
этом перейдет в угол
![]() ,
который эта касательная образует с осью
OX. Поэтому можно утверждать, что
,
который эта касательная образует с осью
OX. Поэтому можно утверждать, что
![]()
где
угол,
образованный касательной к кривой в
точке
![]() и
осью OX.
и
осью OX.
Алгебра производных
Выведем
важнейшие формулы, касающиеся вычисления
производных. В дальнейшем
![]() и
и
![]() -
некоторые функции, у которых существуют
-
некоторые функции, у которых существуют
![]() и
и
![]() ,
а C - некоторая константа (число).
,
а C - некоторая константа (число).
1.
![]()
Доказательство
![]()
2.
![]()
Доказательство
![]()
![]()
Аналогично
выводится формула для
![]() .
.
3.
![]()
Доказательство
![]()
В
числителе дроби прибавим и вычтем
комбинацию
![]()
![]()
![]()
![]()
![]()
4.
Доказательство
![]()
![]()
прибавляем
и вычитаем в числителе комбинацию
![]()
![]()
![]()
![]()
5.
![]()
В
выражении
![]() подразумевается,
что производная от функции
подразумевается,
что производная от функции
![]() берется
так, как будто
берется
так, как будто
![]() является
единым целым (аргументом).
является
единым целым (аргументом).
Доказательство
Пусть
аргумент
получил
приращение
![]() .
Тогда функция >
.
Тогда функция >![]() получила приращение
получила приращение![]() так что
так что
![]() .
Поэтому
.
Поэтому
![]()
делим
и умножаем дробь на
![]()
![]()
Все эти формулы сведены в следующую таблицу, которую следует запомнить (кроме последней формулы).
Таблица 1.
-
Функция
Производная
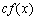

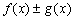
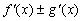
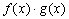
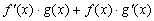
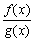
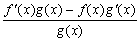
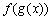
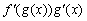
Таблица производных
Выведем теперь таблицу производных от элементарных функций
1.
![]()
Действительно,
если
![]() ,
то
,
то
![]()
2.
![]()
Имеем
![]()
вынесем вверху за скобки

Сделаем
“замену переменных”
![]() .
Тогда
.
Тогда
![]() и
и
![]()
Так как мы получили один из замечательных пределов. Рекомендуется запомнить некоторые частные случаи этой функции этой формулы
а)
![]()
б)
![]()
3.
![]()
Имеем
![]()
так как мы снова имеем один из замечательных пределов.
Особенно
простой результат получается при
![]()
![]()
4.
![]()
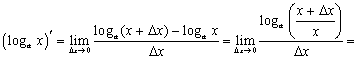
сделаем
“замену переменных”
![]() .
Тогда
.
Тогда
![]() и
и
![]()
Особенно простой результат получается при
![]()
5.
![]()
Имеем
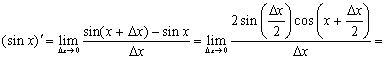
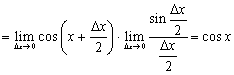
где так же использован замечательный предел.
6.
![]()
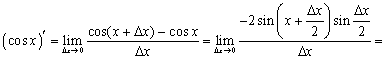
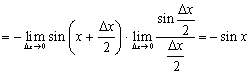
7.
![]()
Так
как
![]() ,
то
,
то
![]()
![]()
8.
![]()
Вывод аналогичен
9.
![]()
В
данном случае
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
Поэтому
.
Поэтому
![]()
10.
![]()
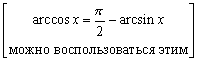
Вывод аналогичен
11.
![]()
В
данном случае
![]() и
и![]() ,
т.е.
,
т.е.
![]() .
Поэтому
.
Поэтому
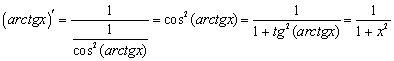
12.
![]()
Вывод аналогичен
Все эти формулы сведены в таблицу, которую следует заучить
Таблица 2
-
функция
производная
1.
2.
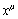
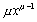
2а.
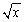
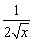
2б.
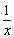
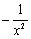
3.
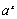
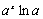
3а.
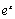
4.
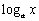
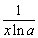
4а.
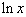
5.


6.
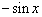
7.
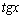
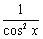
8.


9.
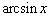
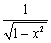
10. arccos x
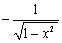
11.
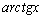
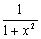
12.
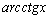
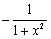
Особые случаи
То,
что в точке
![]() функция
функция
![]() непрерывна
не означает, разумеется, что в этой точке
у нее обязательно существует производная.
Функция может быть непрерывной, а
производной может и не существовать.
Что же там может быть?
непрерывна
не означает, разумеется, что в этой точке
у нее обязательно существует производная.
Функция может быть непрерывной, а
производной может и не существовать.
Что же там может быть?
А. Односторонние производные
Назовем
![]()
производной от функции в точке слева, а
![]()
производной
в той же точке справа.
Разумеется, если
![]() ,
то это означает, что в точке
существует
,
то это означает, что в точке
существует
![]() .
Но могут быть случаи, когда
.
Но могут быть случаи, когда
![]() и
и
![]() существуют,
но не равны друг другу. В этом случае не
существует и
.
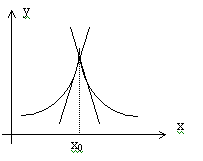
График функции
имеет
в точке
в
этом случае “излом”, и в этой точке к
графику можно провести две касательные
.
существуют,
но не равны друг другу. В этом случае не
существует и
.
График функции
имеет
в точке
в
этом случае “излом”, и в этой точке к
графику можно провести две касательные
.
Б. Бесконечная производная
Рассмотрим
функцию
![]() определенную
для
определенную
для
![]() и
потребуем найти
и
потребуем найти
![]() .
Имеем
.
Имеем
![]()
и производная равна .
Рассматривая
график функции
![]() легко
увидеть, что это означает просто то, что
в точке
легко
увидеть, что это означает просто то, что
в точке
![]() касательная
к графику параллельна оси OY.
касательная
к графику параллельна оси OY.
В. Несуществование производной
Наконец,
может быть ситуация, когда
![]() ,
фигурирующий в определении производной,
не существует.
,
фигурирующий в определении производной,
не существует.
Рассмотрим
для примера,
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Поэтому полагая
.
Поэтому полагая
![]() получим
получим

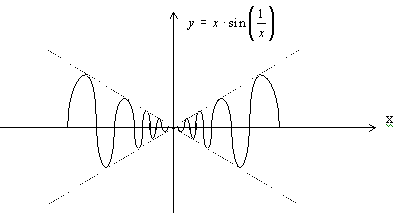
и этот предел просто не существует.
Из графика функции видно, что с приближением к точке касательная колеблется, не стремясь ни к какому определенному положению.
В математике построены даже примеры функций, которые являются непрерывными, но ни в одной точке не имеют производной.
Теоремы Ферма и Ролля
Теорема
Ферма. Пусть функция
определена и непрерывна на промежутке
![]() и
в некоторой внутренней точке
этого
промежутка достигает своего наибольшего
или наименьшего значения, если в этой
точке существует производная, то она
равна нулю:
и
в некоторой внутренней точке
этого
промежутка достигает своего наибольшего
или наименьшего значения, если в этой
точке существует производная, то она
равна нулю:
![]() .
.
Доказательство
Пусть, для определенности, в точке функция достигает своего наибольшего.
По
условию теоремы эта точка внутренняя,
т.е.
![]() ,
и поэтому к этой точке можно подойти и
слева и справа.
,
и поэтому к этой точке можно подойти и
слева и справа.
Пусть мы подходим к слева. Тогда
![]() (т.к.
(т.к.
![]() -
наибольшее значение)
-
наибольшее значение)
![]()
![]() (т.к.
мы подходим слева)
(т.к.
мы подходим слева)
![]()
![]()
Делая
предельный переход
![]() получим
получим
![]()
Пусть мы подходим к точке справа. Тогда
(т.к. - наибольшее значение)
![]() (т.к.
мы подходим слева)
(т.к.
мы подходим слева)
![]()
![]()
Делая предельный переход получим
![]()
Совместить два полученных неравенства можно только в одном случае: . ч.т.д.
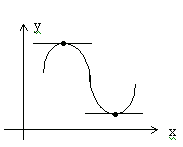
Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX.
Существование ограничений
В
теореме Ферма по сути дела два ограничения:
а) точка
расположена
внутри отрезка
и
б)
![]() .
Покажем, что оба ограничения являются
существенными, т.е. отказ от любого из
них приводит к тому, что утверждение
теоремы становится неверным.
.
Покажем, что оба ограничения являются
существенными, т.е. отказ от любого из
них приводит к тому, что утверждение
теоремы становится неверным.
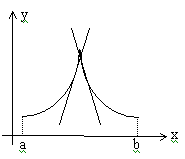
а) “внутренность” точки .

Если максимум или минимум функции достигается на границе отрезка, то утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке только с одной стороны и поэтому не получится второго, противоположного неравенства.
б) существование производной.
Пусть
в точке
существуют
только односторонние производные.
Тогда, как это видно из рисунка, теорема
Ферма неверна. При доказательстве это
проявиться в том, что получаться
неравенства
![]() и
и
![]() ,
которые нельзя будет объединить в одно
равенство, т.к. теперь
,
которые нельзя будет объединить в одно
равенство, т.к. теперь
![]()
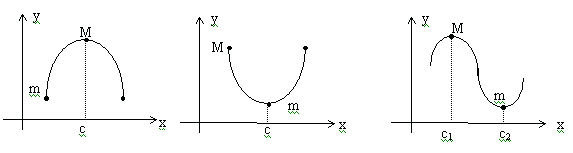
Теорема Ролля. Пусть функция
а) определена и непрерывна на ;
б)
![]() ;
;
в)
![]()
Тогда
существует точка
![]() в
которой
в
которой
![]() .
.
Доказательство этой теоремы следует из такой логической цепочки рассуждений:
1.
Так как
определена
и непрерывна на
,
то, по первой теореме Вейерштрасса, она
ограничена на
,
т.е. существуют конечные
![]() и
и
![]() .
.
2.
Если
![]() ,
то
есть
константа, т.е.
,
то
есть
константа, т.е.
![]() и
поэтому
и
поэтому
![]()
![]() .
В качестве точки c можно взять любую
точку из
.
.
В качестве точки c можно взять любую
точку из
.
3.
Если
![]() ,
то, в силу условия
и
второй теоремы Вейерштрасса, хотя бы
одно из значений
,
то, в силу условия
и
второй теоремы Вейерштрасса, хотя бы
одно из значений![]() или
или
![]() достигается
во внутренней точке промежутка
,по
теореме Ферма, в этой точке (их может
быть и две) производная равна нулю.
достигается
во внутренней точке промежутка
,по
теореме Ферма, в этой точке (их может
быть и две) производная равна нулю.
ч.т.д.
Формулы Коши и Лагранжа
Теорема. Пусть функции и
а) определены и непрерывны на ;
б)
![]() и
и
![]() ;
;
в)
![]()
Тогда существует точка такая, что
![]() .
.
Эта формула носит название формулы Коши.
Доказательство.
Прежде всего отметим, что![]() ,
иначе, по Теореме
Ролля, существовала
бы точка
,
иначе, по Теореме
Ролля, существовала
бы точка
![]() ,
где
,
где
![]() ,
что противоречит ограничению “в”.
,
что противоречит ограничению “в”.
Рассмотрим функцию
![]()
Она
а) определена и непрерывна на , т.к. и функции и непрерывны на
б)
![]()
![]()
в)
![]()
Таким
образом, для
![]() выполнены
все условия Теоремы Ролля. Поэтому
выполнены
все условия Теоремы Ролля. Поэтому
![]() такая,
что
такая,
что
![]() ,
,
но тогда в этой точке
что и дает формулу Коши.
Формула Лагранжа
Рассмотри
частный случай, когда
![]() .
Тогда формула Коши приобретает вид
.
Тогда формула Коши приобретает вид
![]()
или
![]()
где . Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
Заметим, что точка c не обязательно единственная: может быть несколько точек c, удовлетворяющих формулам Коши или Лагранжа.
Рассмотрим
еще вопрос о геометрическом смысле
формулы Лагранжа. Пусть мы имеем график
.
Проведем через точки
![]() и
и
![]() секущую.
Она образует с осью OX угол
секущую.
Она образует с осью OX угол
![]() и
и
![]() .
Но
.
Но
![]() есть
тангенс угла, который касательная к
кривой в точке
есть
тангенс угла, который касательная к
кривой в точке
![]() образует
с осью OX. Поэтому формулу Лагранжа можно
трактовать так: существует точка
,
касательная в которой параллельна
секущей, соединяющей точки
и
.
образует
с осью OX. Поэтому формулу Лагранжа можно
трактовать так: существует точка
,
касательная в которой параллельна
секущей, соединяющей точки
и
.
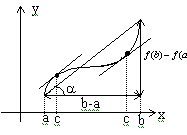
Дифференциал
Рассмотрим важное для дальнейшего понятие дифференциала.
Напомним,
что величина
![]() называется
приращением функции.
называется
приращением функции.
Определение 1. Функция называется дифференцируемой в точке , если ее приращение можно представить в виде
![]()
Определение
2. Линейная часть приращения функции,
т.е.
![]() называется
дифференциалом функции
и
обозначается
называется
дифференциалом функции
и
обозначается
![]()
![]()
Чтобы
точно уяснить эти определения функции
рассмотрим пример. Пусть
![]() .
Тогда
.
Тогда
![]()
Заметим,
что
![]() содержит
слагаемое, линейное по
содержит
слагаемое, линейное по
![]() ,
слагаемые с
,
слагаемые с
![]() и
и
![]() .
Так вот, только слагаемое, линейное по
дает
дифференциал, т.е.
.
Так вот, только слагаемое, линейное по
дает
дифференциал, т.е.
![]()
Теорема о дифференцируемости функций
Для
того, чтобы функция
была
дифференцируемой в точке
,
необходимо и достаточно, чтобы в этой
точке существовала производная
.
При этом
![]() .
.
Доказательство
Необходимость. Пусть дифференцируема в точке . Это значит, что
Деля на
![]()
и
переходя к пределу
![]() ,
получим
,
получим
![]()
Достаточность. Пусть в точке существует производная
![]()
Это, по определению, означает, что
![]()
где - бесконечно малая величина. Отсюда следует, что
![]()
Но
![]() и
поэтому
и
поэтому
![]()
что и требовалось доказать.
Выражение для дифференциала
Итак, мы получили, что для дифференцируемой функции . Это означает, что
![]() .
.
Но
если взять
![]() ,
то мы получим, что
,
то мы получим, что
![]() ,
т.е. дифференциал независимой переменной
равен ее приращению. Поэтому окончательно
,
т.е. дифференциал независимой переменной
равен ее приращению. Поэтому окончательно
![]()
Отсюда следует, что
![]()
т.е.
производная есть отношение дифференциала
функции к дифференциалу независимой
переменной. Заметьте, что
![]() есть
обычная дробь и с ней можно обращаться
как с обычной дробью.
есть
обычная дробь и с ней можно обращаться
как с обычной дробью.
Геометрический смысл дифференциала
Вспомним,
что
есть
тангенс угла наклона касательной к оси
OX. Поэтому, если провести касательную
к кривой в точке
,
то
![]() будет
катетом, который противолежит углу
в
треугольнике, гипотенуза которого
образована касательной, а другой катет
есть приращение
будет
катетом, который противолежит углу
в
треугольнике, гипотенуза которого
образована касательной, а другой катет
есть приращение
![]() На
рисунке нарисован и отрезок
На
рисунке нарисован и отрезок
![]() ,
так что видно отличие
и
.
,
так что видно отличие
и
.

Правила дифференцирования
Пользуясь
формулой
![]() выведем
несколько важных формул, касающихся
дифференциалов.
выведем
несколько важных формул, касающихся
дифференциалов.
1.
![]()
Действительно
![]()
2.
![]()
Имеем
![]()
![]()
3.
![]()
Имеем
![]()
![]()
4.
![]()
Имеем
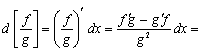
![]() .
.
5.
![]()
Имеем
![]()
В качестве приложения понятия дифференциала выведем формулу для производной от функций заданных параметрически.
Параметрическое
задание функции заключается в том, что
и
и
задаются
как функции некоторого параметра
![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
Значение параметра определяет одновременно и и , и, тем самым, некоторую точку на плоскости. Меняя мы двигаем точку на плоскости и она описывает некоторую кривую, определяющую зависимость от . Параметрическое задание функции считается самым общим способом задания кривых на плоскости.
Имеем
![]()
![]()
Отсюда производная от по имеет вид
![]()
![]()
Сокращая
на
![]() получим
окончательно
получим
окончательно
![]()
Производные и дифференциалы высших порядков.
Пусть
имеется функция
,
от которой мы вычислили первую производную
.
Но
снова
является функцией и от нее можно тоже
вычислить производную. Производная от
первой производной т.е.
![]() называется
второй производной и обозначается
называется
второй производной и обозначается
![]() :
:
![]()
Аналогично, производная от второй производной называется третьей производной
![]() .
.
Аналогично
определяются производные более высоких
порядков. Отметим только, что производные
более высоких порядков отмечаются не
штрихами (их было бы слишком много) а
цифрами, заключенными в скобки -
![]() ,
,
![]() и
т.д.
и
т.д.
Итак, производная n-го порядка определяется как производная от производной (n-1)-го порядка
![]()
Основные формулы, касающиеся производных высших порядков, следующие:
1.
![]()
2.
![]()
3.
![]()
Первые
две формулы очевидны. Третью формулу,
носящую название формулы Лейбница, мы
доказывать не будем. При ее применении
следует только иметь ввиду, что производной
нулевого порядка считается сама функция,
т.е.
![]() .
.
Аналогично этому, дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.
![]()
Выведем
формулу для
![]() .
Имеем
.
Имеем
![]()
При
дальнейшем преобразовании следует
иметь в виду, что
![]() ,
совпадающее с приращением аргумента
,
есть величина, совершенно не зависимая
от
,
т.к. мы
можем
взять каким угодно. Поэтому по отношению
к
,
совпадающее с приращением аргумента
,
есть величина, совершенно не зависимая
от
,
т.к. мы
можем
взять каким угодно. Поэтому по отношению
к
![]() .
.
Скобки
у
![]() обычно
не пишут
обычно
не пишут
![]()
Отсюда
![]()
Аналогично, дифференциал третьего порядка определяется как дифференциал от второго дифференциала
![]()
Имеем
![]()
![]()
так что
![]() ;
;
![]()
В общем случае
![]()
Легко показывается по индукции, что
![]() ;
;
![]() .
.
Функции нескольких переменных
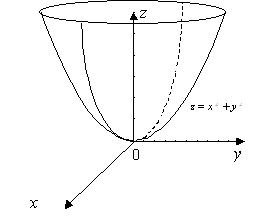
Определение. Переменная z называется функцией переменных х и у, если каждой паре значений х и у в некоторой области их изменения поставлено в соответствие одно значение z. Функциональную зависимость z от х и у записывают в виде: z=f(x,у). Это уравнение определяет некоторую поверхность в пространстве R3.
Геометрическим
образом функции z=x2+y2
является параболоид. Пусть z=a,
тогда x2+y2=a,
т.е. линия пересечения плоскости z=
a с поверхностью
z=x2+y2
есть окружность x
2+
y 2=
a радиуса
![]() .
Пусть у=0,
тогда z=x2
и, следовательно, при пересечении
плоскости Oхz
с поверхностью получается парабола.
Метод сечений дает возможность лучше
представить себе геометрический образ
данной функции.
.
Пусть у=0,
тогда z=x2
и, следовательно, при пересечении
плоскости Oхz
с поверхностью получается парабола.
Метод сечений дает возможность лучше
представить себе геометрический образ
данной функции.
Определение. Число А называется пределом функции z=f(x,у) в точке М0(х0, у0), если для каждого числа ε>0 найдется такое число β>0, что для всех точек М(х,у), для которых выполняется неравенство |ММ0|<β, будет выполняться неравенство | f(x,у)– A|< ε
Обозначим
![]() .
.
Определение.
Функция z=f(x,у)
называется непрерывной в точке М0(х0,у0),
если имеет место равенство
![]() .
.
5. Частные производные и полный дифференциал 1-го порядка
Определение.
Производная от функции z=f(x,у)
по х,
найденная в предложении, что у
остается постоянным, называется частной
производной от z
по х
и обозначается
![]() или
f'x
(x,у).
Аналогично определяется и обозначается
частная производная z
по у.
или
f'x
(x,у).
Аналогично определяется и обозначается
частная производная z
по у.
Если функция z=f(x,у) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть представлено в виде:
![]() ,
(7.1)
,
(7.1)
где
![]() при
при
![]() .
.
Определение.
Выражение
![]() является
главной частью полного приращения Δz
и называется полным дифференциалом
функции z=f(x,у)
и обозначается dz:
является
главной частью полного приращения Δz
и называется полным дифференциалом
функции z=f(x,у)
и обозначается dz:
![]() .
(7.2)
.
(7.2)
Полагая
в формуле (2) z
равным х,
найдем
![]() ,
а при z=y
,
а при z=y
![]() .
Поэтому
.
Поэтому
![]() .
(7.3)
.
(7.3)
Из
(7.1) следует, что
![]() .
.
Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.
6. Градиент функции. Производная по направлению
Определение.
z=f(x,у)
дифференцируемая функция двух переменных.
Тогда вектор
![]() называется
градиентом функции z=f(x,у).
называется
градиентом функции z=f(x,у).
Он обладает следующими свойствами:
![]()
![]()
![]()
Пусть
![]() –
направляющие косинусы некоторого
вектора
–
направляющие косинусы некоторого
вектора
![]() ,
т.е.
,
т.е.
![]() .
Тогда
.
Тогда
![]() –
производная функции z=f(x,у)
в данном направлении
.
–
производная функции z=f(x,у)
в данном направлении
.
7. Экстремум функции двух переменных
Определение. Функция z=f(x,у) имеет в точке М0(х0,у0) максимум, если в окрестности этой точки выполняется равенство f(x,у)<f(x0,у0).
Аналогично определяется минимум функции z=f(x,у) в точке М0(х0, у0).
Необходимый признак экстремума
Если М (х0,у0) – точка экстремума дифференцируемой функции z=f(x,у)), то
![]() то
есть
то
есть
![]()
Достаточный признак экстремума
Пусть
z=f(x,у)
– функция, для которой существуют
производные первого и второго порядка
в точке М(х0,у0):
![]()
![]()
![]() .
Составим выражение Δ=АС–В2.
.
Составим выражение Δ=АС–В2.
Если Δ>0, то М(х0, у0) – точка экстремума, а именно: точка максимума при A<0 (если C<0), точка минимума при A>0 (или С>0). Если Δ<0, то в точке М нет экстремума.
