Блок самопроверки

Пример 1.

Найти производную функции

Пример 2.

Найти производную функции

Пример 3.

Найти производную функции

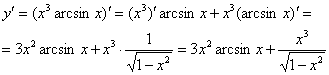
Пример 4.

Найти производную функции

Пример 5.

Найти производную функции

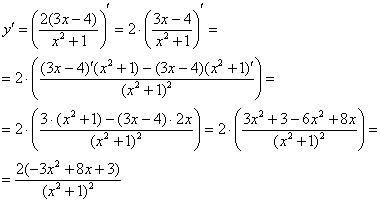
Пример 6.

Найти производную функции

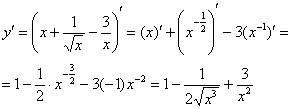
Пример 7.

Найти производную функции

Пример 8.

Найти производную функции

Пример 9.

Найти производную функции

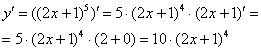
Пример 10.

а) Найти производную функции

б) Найти производную функции

Пример 11.

Найти производную функции

Пример 12.

Найти производную функции

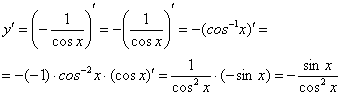
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила 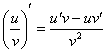, ответы должны совпасть.

Пример 13.

Найти производную функции

Пример 14.

Найти производную функции

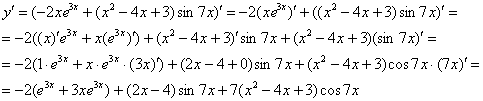
Пример 15.

Найти полный дифференциал функции .

Решение. Сначала найдем частные производные

Производная  найдена в предположении, что у постоянна, а  найдена в предположении, что х постоянна. По формуле (7.3):

Ответ. dz=(10 x–6xy³) dx+(9 x² y²+6) dy.

Список литературы

1. Балдин, К.В. Краткий курс высшей математики / К.В.Балдин, Ф.К.Балдин, В.И.Джеффаль – М.: Дашков и Ко, 2009 (электронный ресурс «Университетская библиотека»);

2. Малыхин, В.И. Высшая математика: Учебное пособие / В.И.Малыхин – М.: Инфра-М, 2009 (электронный ресурс «Университетская библиотека»);

3. Самарин, Ю.П. Высшая математика / Ю.П.Самарин, Г.А.Сахабиева, В.А.Сахабиев – М.: Машиностроение, 2006 (электронный ресурс «Университетская библиотека»).

Глава 8. Интеграл, его свойства, вычисление площадей и объемов фигур

Основные методы интегрирования

Функция F( x ), дифференцируемая в данном промежутке X, называется первообразной для функции f ( x ), или интегралом от f ( x ), если для всякого x Î X справедливо равенство:

F ¢ (x) = f(x).                                              (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f ( x ) на данном промежутке Х называется множество всех первообразных функций для функции f ( x ); обозначение -

ò f( x) dx .

Если F( x ) - какая-нибудь первобразная для функции f ( x ), то

ò f( x) dx = F(x) + C,                                         (8.2)

где С - произвольная постоянная.

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

d ò f(x)=f(x) dx ,

ò df ( x)=f(x)+C,

ò af ( x) dx =a ò f(x) dx (a=const),

ò ( f( x)+g(x)) dx = ò f(x) dx + ò g(x) dx .

Список табличных интегралов

ò x ^m dx = x ^{m +1} /( m + 1) +C ( m ¹ -1).

= ln ê x ê +C.

ò a ^x dx = a ^x / ln a + C (a>0, a ¹ 1).

ò e ^x dx = e ^x + C.

ò sin x dx = cos x + C.

ò cos x dx = - sin x + C.

= arctg x + C.

= arcsin x + C.

= tg x + C.

= - ctg x + C.

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f ( z ) непрерывна на [ a , b ], функция z=g ( x ) имеет на [ a,b ] непрерывную производную и a £ g ( x ) £ b , то

ò f( g(x)) g ¢ (x) dx = ò f(z) dz ,                                   (8.3)

причем после интегрирования в правой части следует сделать подстановку z=g ( x ).

Для доказательства достаточно записать исходный интеграл в виде:

ò f( g(x)) g ¢ (x) dx = ò f(g(x)) dg(x).

Например:

;

.

Пусть u = f ( x ) и v = g ( x ) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,

d ( uv )= udv + vdu или udv = d ( uv ) - vdu .

Для выражения d ( uv ) первообразной, очевидно, будет uv , поэтому имеет место формула:

ò udv = uv - ò vdu .                                                       (8.4)

Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx .

Пусть, например, требуется найти ò x cosx dx . Положим u = x , dv = cos x dx , так что du=dx , v=sinx . Тогда

ò x cos x dx = ò x d(sin x) = x sin x - ò sin x dx = x sin x + cos x + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

ò x ^k ln ^m x dx , ò x ^k sin bx dx , ò x ^k cos bx dx , ò x ^k e ^ax dx

и другие, которые вычисляются именно с помощью интегрирования по частям.

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке [ a , b ] определена функция f ( x ). Разобьем отрезок [ a , b ] на n частей точками a = x ₀ < x ₁ <...< x _n = b . Из каждого интервала ( x _{i - 1} , x _i ) возьмем произвольную точку x _i и составим сумму f ( x _i ) D x _{i ,} где

D x _i = x _i - x _{i - 1} . Сумма вида f ( x _i ) D x _i называется интегральной суммой, а ее предел при l = max D x _i ® 0, если он существует и конечен, называется определенным интегралом функции f ( x ) от a до b и обозначается:

  f( x _i ) D x _i.                                           (8.5)

Функция f ( x ) в этом случае называется интегрируемой на отрезке [ a , b ], числа a и b носят название нижнего и верхнего предела интеграла.

Для определенного интеграла справедливы следующие свойства:

;

;

- ;

, (k = const, k Î R );

;

;

f( x )(b-a) ( x Î [ a,b ]).

Последнее свойство называется теоремой о среднем значении.

Пусть f ( x ) непрерывна на [ a , b ]. Тогда на этом отрезке существует неопределенный интеграл

ò f( x) dx = F(x) + C

и имеет место формула Ньютона-Лейбница, c вязывающая определенный интеграл с неопределенным:

  F( b) - F(a).                                                 (8.6)

Геометрическая интерпретация: определенный интеграл  представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f ( x ), прямыми x = a и x = b и отрезком оси Ox .

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:

.                                          (8.7)

Если этот предел существует и конечен, то  называется сходящимся несобственным интегралом от f ( x ) на интервале [ а,+ ¥ ), а функцию f ( x ) называют интегрируемой на бесконечном промежутке [ а,+ ¥ ). В противном случае про интеграл  говорят, что он не существует, или расходится.

Аналогично определяются несобственные интегралы на интервалах (- ¥ , b ] и (- ¥ , + ¥ ):

.

Определим понятие интеграла от неограниченной функции. Если f ( x ) непрерывна для всех значений x отрезка [ a,b ], кроме точки с , в которой f ( x ) имеет бесконечный разрыв, то несобственным интегралом II рода от f ( x ) в пределах от a до b называется сумма:

,

если эти пределы существуют и конечны. Обозначение:

 = .                               (8.8)