1. Проективная прямая.

Пусть a и a – две пересекающиеся прямые, а S – точка, лежащая вместе с ними в одной плоскости, S  a, S  a. Рассмотрим проецирование прямой a на прямую a из точки S. Пусть A  a, SA  a . Тогда точка A не имеет проекции.

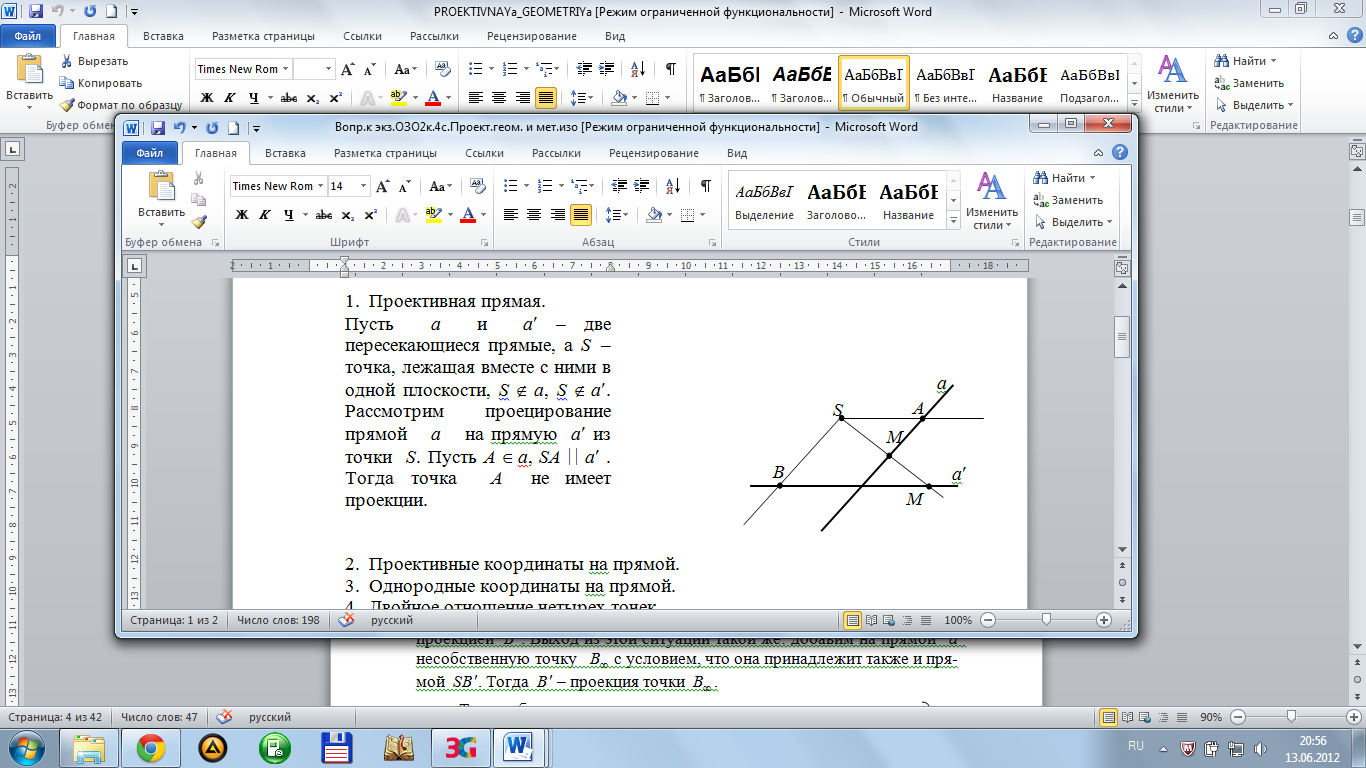
На a(несобственная a и SA) добавляется новая точка A_ , которая одновременно принадлежит прямой SA . A_ будет проекцией точки A . Аналогично, если B  a и SB  a , то на a не существует точки с проекцией B . Добавим на прямой a несобственную точку B_ и принадлеж. SB . Тогда B  – проекция точки B_ .

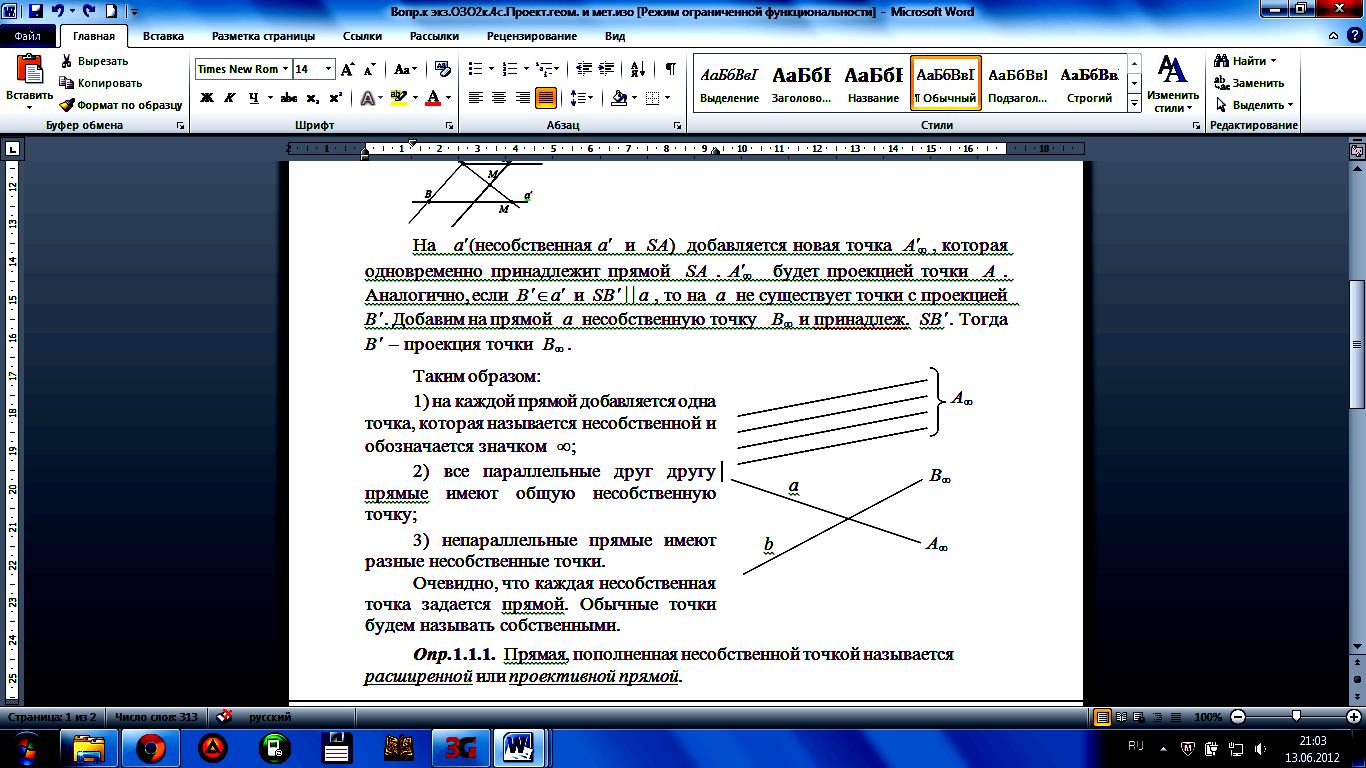
Таким образом:

1) на каждой прямой добавляется одна точка, которая называется несобственной и обозначается значком ;

2) все параллельные друг другу прямые имеют общую несобственную точку;

3) непараллельные прямые имеют разные несобственные точки.

Очевидно, что каждая несобственная точка задается прямой. Обычные точки будем называть собственными.

Прямая, пополненная несобственной точкой называется расширенной или проективной прямой. Прямую a, расширенную несобственной точкой A_ , будем обозначать a; ¯ ; a; ¯ = a  A_ . Центральное проецирование расширенной прямой на расширенную прямую – взаимнооднозначное отображение.

2. Проективные координаты на прямой.

Проективной системой координат (проективным репером) на проективной прямой a; ¯ называется произвольная упорядоченная тройка точек этой прямой.

Проективный репер обычно обозначается буквой R , а точки, из которых он состоит – A₁, A₂ , E . Причем E называется единичной точкой репера. Однородные координаты на прямой.

Говорим, что вектор x;\s\up8(( порождает точку M на прямой a; ¯если x;\s\up8(( лежит на прямой OM.

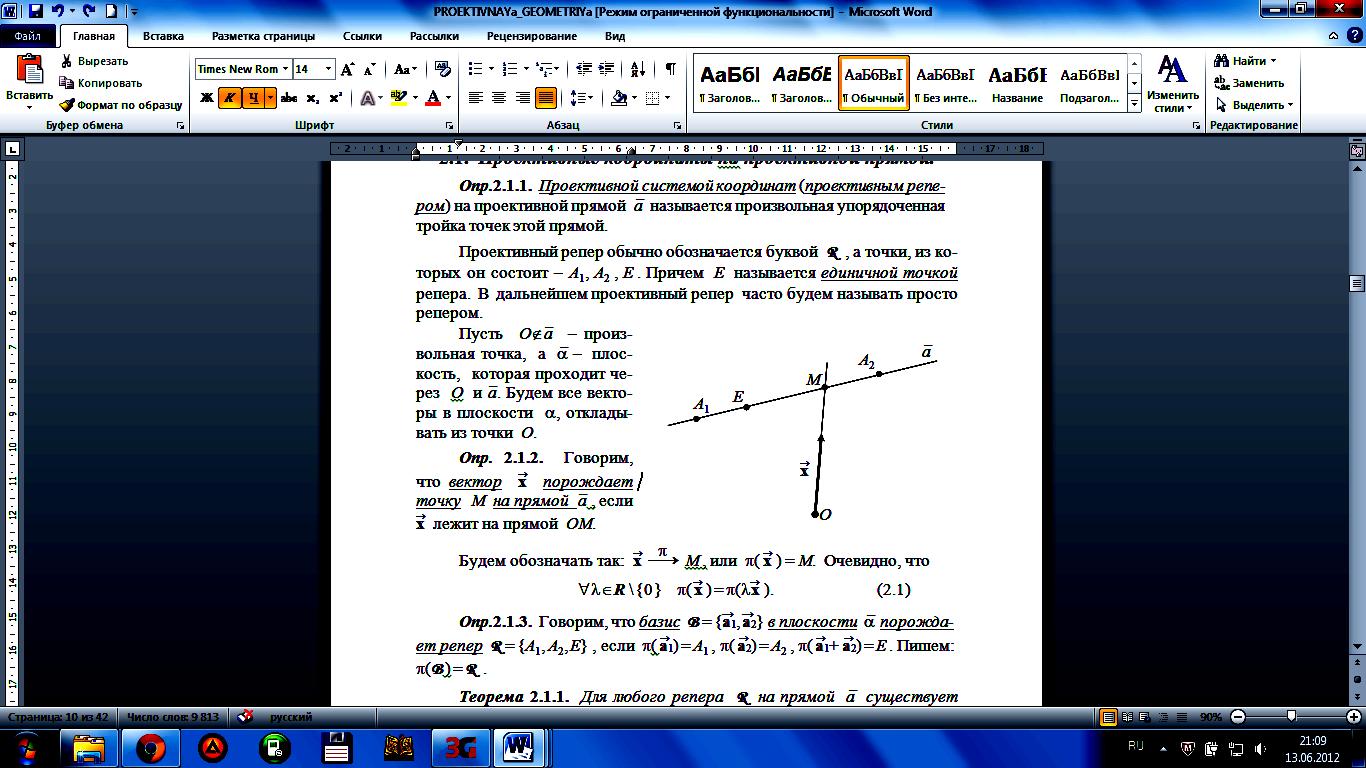
x;\s\up8(( ((;\s\up8(( M , или ( x;\s\up8(( ) = M. Очевидно, что

R \{0} ( x;\s\up8(( ) = (x;\s\up8(( ).

базис B = {a1;\s\up8(–( , a2;\s\up8(–( } в плоскости (; ¯ порождает репер R = {A₁, A₂, E} , если ( a1;\s\up8(( ) = A₁ , ( a2;\s\up8(( ) = A₂ , ( a1;\s\up8(( + a2;\s\up8(( ) = E . Пишем: (B ) = R .

Теорема. Для любого репера R на прямой a; ¯ существует единственный с точностью до гомотетии с центром O базис B, который порождает репер R .

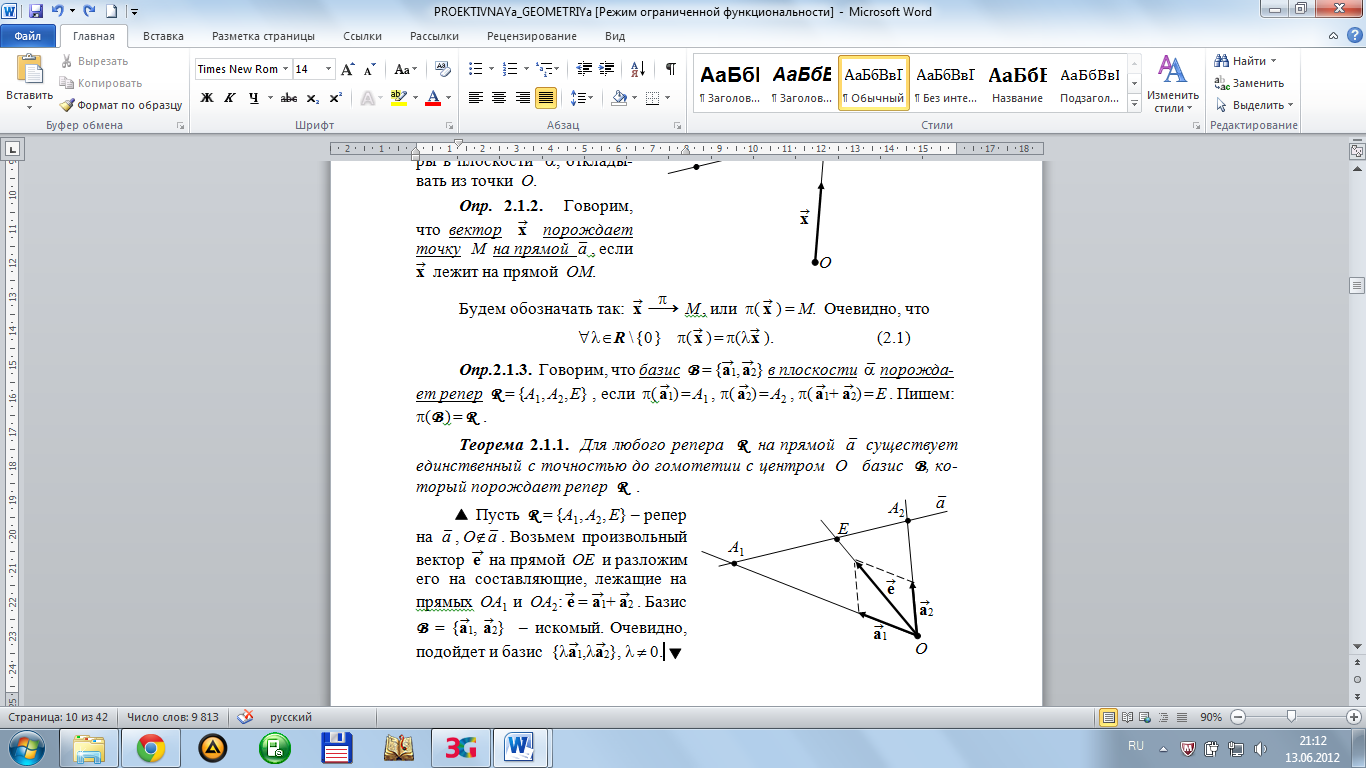Пусть базис B порождает репер R , а вектор x;\s\up8(( – точку M. Проективными координатами точки M на прямой a; ¯ в репере R называются координаты вектора x;\s\up8(–( относительно базиса B .

Данная точка в данном репере имеет не одну пару координат (x₁, x₂), а множество пар, пропорциональных друг другу.

Таким образом, для того, чтобы найти координаты (x₁, x₂) точки Ma; ¯ в репере R , необходимо:

1. выбрать собственную точку Oa; ¯;

2. выбрать базис B , который порождает R ;

3. выбрать вектор x;\s\up8(( на прямой OM ;

4. найти координаты (x₁, x₂) этого вектора в базисе B (они и будут

проективными координатами точки M, т.е. M(x₁: x₂)).

Проективные координаты в репере, одна точка которого несобственная, называются однородными аффинными координатами на прямой.

3. Однородные координаты на прямой.

Очень простой смысл имеют проективные координаты в репере, первая точка которого несобственная. Пусть R = {A_1 , A₂, E} – такой репер

и M – произвольная собственная точка на прямой a; ¯ . Тогда прямая OA_1 a; ¯ . Обозначим

e;\s\up8(( = OE;\s\up10( –(, e1;\s\up8(( = A2E;\s\up10( –( , e2;\s\up8(( = OA2;\s\up10( –( , x;\s\up8((= OM;\s\up10( –( .

Тогда A2M;\s\up10( –( e1;\s\up8(( , т.е. xR: A2M;\s\up10( –(= xe1;\s\up8(( .

Поэтому

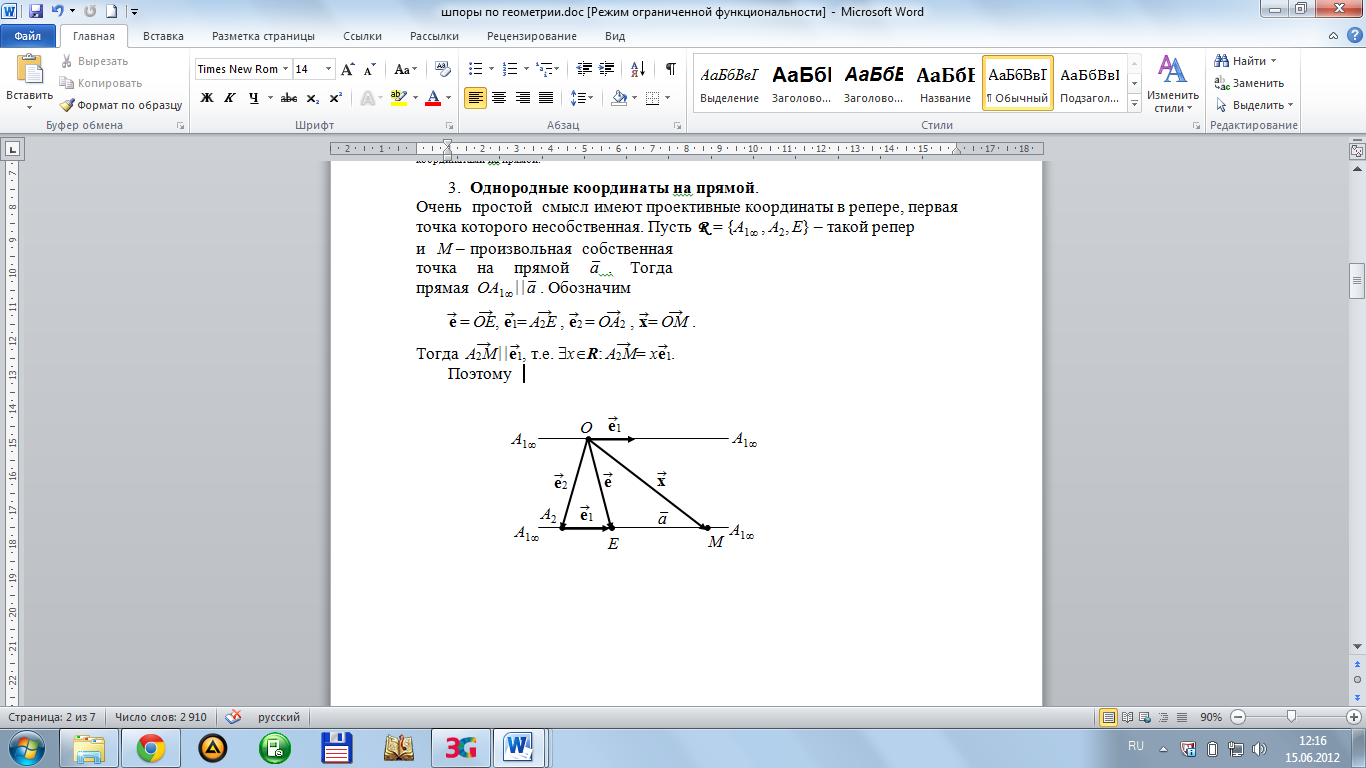
x;\s\up8(( = OA2;\s\up10( –( + A2M;\s\up10( –( = xe1;\s\up8(( + e2;\s\up8(( .

Значит, проективные координаты x₁: x₂ точки M в таком репере будут x:1, где x – обычная координата точки M в аффинной системе координат на прямой a; ¯ с началом A₂ и единичной точкой E . На рисунке M(3:1).

Проективные координаты в репере, одна точка которого несобственная, называются однородными аффинными координатами на прямой.