9. Свойства сходящихся рядов.

• Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

• Е 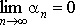сли ряд сходится, то

• Если ряд сходится, то сходится ряд и имеет место равенство.

.

10. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость ряда.

Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков. Знакочередующиеся ряды

Переходя к рассмотрению рядов, члены которых уже не обязательно положительны, остановимся сначала на одном важном частном типе этих рядов - на рядах знакочередующихся, теория которых сравнительно проста.

Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.

Несколько изменяя употреблявшуюся выше символику, будем обозначать через an не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме a1 - a2 + a3 - a4 + a5 - ... (36... a1 + (-a2) + a3 + (-a4) + ...)

Признак Лейбница: Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.Или в два пункта:

1) Ряд является знакочередующимся. 2) Члены ряда убывают по модулю. То есть,

Абсолютной сходимости.Говорят, что ряд an - сходится абсолютно, если ряд an сходится.

В случае, когда an - знакоположительный ряд, имеем /an/  an при всех n , и поэтому в таком случае абсолютная сходимость совпадает с обычной.

условной сходимости. Говорят, что ряд аn сходится условно, если он сходится, но не абсолютно.

Примером условно сходящего ряда является знакочередующийся гармонический ряд.

Следующая теорема утверждает, что обратная ситуация невозможна.

11. Понятие о функциональных рядах. Степенные ряды. Радиус сходимости степенного ряда.

Ф ункциональный ряд

Пусть – функции комплексной переменной z. Ряд

носит название функционального ряда.

С тепенные ряды являются частным случаем функциональных рядов. Степенным рядом называется функциональный ряд вида где an - коэффициенты степенного ряда,x0 - центр ряда.

Теорема о радиусе сходимости.

Для каждого степенного ряда существует 0=<R=<бесконечности, удовлетворяющее свойствам:

Если R=0, то ряд сходится только при x=0 .

Если R=бесконечности, то ряд сходится при любых x€(-бесконечности;+бесконечности).

Если 0<R<бесконечности, то ряд сходится при x€(-R;R) и расходится при х непринадлежащем[-R;R].

Сходимость на любом отрезке внутри интервала (-R;R)равномерная.

Число R - радиус сходимости степенного ряда.