
- •Глава I. Аналитическая геометрия………………………………………….……4
- •Карточка.
- •Глава I. Аналитическая геометрия.
- •1.1 Векторы
- •1.2 Прямая и плоскость.
- •1.3 Задачи на нахождение уравнения прямой/плоскости.
- •Делаем чертеж:
- •1.4 Задачи на угол м/у прямыми, плоскостями, прямой и плоскостью.
- •1.5 Задачи на точку пересечения прямых, прямой и плоскости.
- •1.6 Задачи на проекцию.
- •1.7 Задачи на симметрию.
- •Глава II. Матрицы
- •2.1 «Тривиальные» действия
- •2.2Ранг матрицы
- •2.3 Определитель матрицы.
- •2.4 Обратная матрица.
- •2.5 Совместность. Зависимость. Базис
- •2.6 Системы уравнений.
- •2.7 Собственные векторы.
- •Глава III. Пределы.
- •Глава IV. Производные и дифференциалы.
- •4.1 «Тривиальные» производные.
- •4.2 Уравнения касательной и нормали к графику функций.
- •1) Производная в точке, заданная неявно.
- •Уравнение касательной к графику функций в точке.
- •Уравнение нормали к графику функций.
- •4.3 Производная функции нескольких переменных.
- •4.4 Градиент. Производная по направлению.
- •4.5 Первый и второй дифференциал.
- •4.6 Касательная плоскость.
- •4.7 Формулы Тейлора и Маклорена.
- •Глава V. Интегралы.
- •5.1 Свойства интегралов и таблица первообразных.
- •5.2 Метод частичной замены переменной.
- •5.3 Метод замены переменной.
- •5.4 Определенный интеграл.
- •5.5 Двойные интегралы.
- •Глава VI. Точки экстремума функции нескольких переменных.
- •6.1 Локальный экстремум функции.
- •6.2 Локальный условный экстремум.
- •6.3 Метод Лагранжа.
2.6 Системы уравнений.
4.2
(а)
Найдите фундаментальную систему решений:

Алгоритм решения:
Записать в виде матрицы и привести к треугольному виду (при этом стоит над каждым столбцом подписывать соответствующую переменную, чтобы избежать путаницы):

 .
.
Начиная с нижней строки, начинаем находить переменные, записывая строку в виде уравнения. Если в уравнении больше одной переменной, то берем одну из переменных за t (если в одном уравнении три переменных, то вводим 2 переменные). Берем за t ту переменную, перед которой стоит наибольший по модулю коэффициент (в данном примере этот коэффициент -2, а значит, обозначаем за доп. переменную
 ):
):

Записываем ответ в формате:
Ответ:
 .
.
4.6.(а)
Представьте общее решение в виде суммы
частного решения и общего решения
соответствующей однородной системы:

Решение:
Записываем в виде матрицы и приводим к треугольному виду:
 .
.
Начиная с нижней строки, начинаем решать. В нижней строке у нас три переменных (при одном уравнении), значит нужно заменить 2 переменные: и
 (т.к. перед ними наибольшие коэффициенты):
(т.к. перед ними наибольшие коэффициенты):


Записываем ответ в формате:
Ответ:
 .
.
P.S. в первых строках мы пишем элементы из , во вторых из и т.д.
2.7 Собственные векторы.
 .
Где
.
Где
 -
исходная матрица,
-
исходная матрица,
 - собственный ненулевой вектор,
- собственный ненулевой вектор,

 -
собственное значение, Е – единичная
матрица
-
собственное значение, Е – единичная
матрица

 .
.
Нахождение соб. вектора делается в два шага:
Нахождение собственного значения. Для этого
 ,
т.е.
,
т.е.
 =0
=0
Нахождения соб. вектора. Для этого в матрицу вида:

Подставляем собственное значение (если их несколько находим для каждого соб. вектор) и находим вектор .
Пример:
5.3(а)
Найдите
собственные векторы и собственные
значения матрицы:
 .
.
Решение:
 P.S.
Определитель нашли через метод миноров
и алгебраических дополнений.
P.S.
Определитель нашли через метод миноров
и алгебраических дополнений.А)


 .
.
P.S.
т.к. у нас во всем примере нет ни одного
коэффициента при ,
это не значит, что он равен нулю, поэтому
его необходимо записать через новый
параметр
,
это не значит, что он равен нулю, поэтому
его необходимо записать через новый
параметр .
.
Б)


 5.4.
При
каком значении параметра
5.4.
При
каком значении параметра
 матрица
матрица
 имеет собственный вектор
имеет собственный вектор
 ,
соответствующий собственному значению
,
соответствующий собственному значению
 ?
?
Совет:
В
задачах подобных этой мы не используем
первый шаг. Мы сразу записываем матрицу
 и если у нас есть
и если у нас есть
 ,
то подставляем его, записываем матрицу
в виде системы и подставляем координаты
иксов.
,
то подставляем его, записываем матрицу
в виде системы и подставляем координаты
иксов.
P.S. если не дано, то все равно подставляем иксы и решаем системы с двумя неизвестными ( и а).
Решение:
На самом деле этот пример легче предыдущего, т. к. нам не нужно искать соб. значение – оно нам уже дано. Запишем сразу второй шаг:
 .
Записываем нашу матрицу в виде системы
и подставим
:
.
Записываем нашу матрицу в виде системы
и подставим
:


Теперь, вместо иксов подставим их значения из вектора, данного в условии:
 Ответ:
а=3.
Ответ:
а=3.
Глава III. Пределы.
Для
начала напомним, что:

 ;
; ;
;
 - неопределенности. Для того, чтобы
определить какого типа перед нами
неопределенность (если она вообще есть),
необходимо для начала подставить
значение
- неопределенности. Для того, чтобы
определить какого типа перед нами
неопределенность (если она вообще есть),
необходимо для начала подставить
значение
 ,
к которому стремится х.
,
к которому стремится х.
Условно можно разбить способы нахождения пределов на несколько типов, относительно неопределенности:
Неопределенность типа
 .
.
Для того чтобы найти пределы подобного вида, необходимо вынести из числителя и знаменателя х в наибольшей степени, а затем сократить и подставить значение .
Примеры:
6.3
 .
.
Решение:

6.8 .
.
Решение:
Видно,
что максимальная степень, которую можно
вынести из числителя -
 (при вынесении из-под корня
(при вынесении из-под корня
 образуется
как
образуется
как
 ).
).
Максимальная степень, которую можно вынести из знаменателя - (при одновременном вынесении из-под корня и из скобки n образуется ).

Неопределенность типа
 .
.
Почти
всегда неопределенность данного вида
имеет вид разности корней. Для решения
необходимо домножить выражение на
сопряженное (т.е. разность корней умножить
на их сумму) по правилу: .
.
Пример:
6.20
 .
.
Решение:


 .
.
Неопределенность типа
 .
.
Для
решения данного типа неопределенности
необходимо из числителя и знаменателя
вынести
 через деление столбиком, затем сократить
и, подставив
через деление столбиком, затем сократить
и, подставив
 ,
найти предел.
,
найти предел.
Пример:
7.1(б)
 .
.
Решение:



Второй замечательный предел.
Обычно
второй замечательный предел после
упрощений выглядит так:
 ,
где k
стремится к бесконечности, а
,
где k
стремится к бесконечности, а
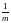 к нулю. Раскрывается он следующим
образом:
к нулю. Раскрывается он следующим
образом:
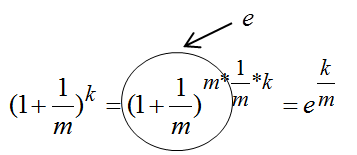 .
.
Пример:
6.32 .
.
Решение:



 .
.
Правило Лопиталя.
Для
раскрытия неопределенностей типа
 или
или
 ,
можно использовать правило Лопиталя:
,
можно использовать правило Лопиталя:
 ,
при условии, что
,
при условии, что
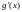
 и
и
 -
дифференцируемы в окрестности
-
дифференцируемы в окрестности
 .
.
Пример:
7.1(в)
 .
.
Решение:
 .
.
