
- •Глава I. Аналитическая геометрия………………………………………….……4
- •Карточка.
- •Глава I. Аналитическая геометрия.
- •1.1 Векторы
- •1.2 Прямая и плоскость.
- •1.3 Задачи на нахождение уравнения прямой/плоскости.
- •Делаем чертеж:
- •1.4 Задачи на угол м/у прямыми, плоскостями, прямой и плоскостью.
- •1.5 Задачи на точку пересечения прямых, прямой и плоскости.
- •1.6 Задачи на проекцию.
- •1.7 Задачи на симметрию.
- •Глава II. Матрицы
- •2.1 «Тривиальные» действия
- •2.2Ранг матрицы
- •2.3 Определитель матрицы.
- •2.4 Обратная матрица.
- •2.5 Совместность. Зависимость. Базис
- •2.6 Системы уравнений.
- •2.7 Собственные векторы.
- •Глава III. Пределы.
- •Глава IV. Производные и дифференциалы.
- •4.1 «Тривиальные» производные.
- •4.2 Уравнения касательной и нормали к графику функций.
- •1) Производная в точке, заданная неявно.
- •Уравнение касательной к графику функций в точке.
- •Уравнение нормали к графику функций.
- •4.3 Производная функции нескольких переменных.
- •4.4 Градиент. Производная по направлению.
- •4.5 Первый и второй дифференциал.
- •4.6 Касательная плоскость.
- •4.7 Формулы Тейлора и Маклорена.
- •Глава V. Интегралы.
- •5.1 Свойства интегралов и таблица первообразных.
- •5.2 Метод частичной замены переменной.
- •5.3 Метод замены переменной.
- •5.4 Определенный интеграл.
- •5.5 Двойные интегралы.
- •Глава VI. Точки экстремума функции нескольких переменных.
- •6.1 Локальный экстремум функции.
- •6.2 Локальный условный экстремум.
- •6.3 Метод Лагранжа.
Глава IV. Производные и дифференциалы.
4.1 «Тривиальные» производные.

Таблица сложных производных



Примеры на нахождение производной:
8.3

Решение:

8.12

Решение:

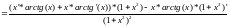

8.21
 .
.
Решение:
Проблема
этого примера в том, что мы не знаем
производной функции типа:
 ,
поэтому необходимо сделать следующие
преобразования:
,
поэтому необходимо сделать следующие
преобразования:
 .
.
P.s. это основное логарифмическое тождество.
 =
=

 .
.
4.2 Уравнения касательной и нормали к графику функций.
1) Производная в точке, заданная неявно.
Пример:
8.26
Найдите
значение производной
 функции
функции
 ,
заданной неявно уравнением
,
заданной неявно уравнением
 ,
в точке М(0; 1).
,
в точке М(0; 1).
Решение:
Для
решения данного примера необходимо
взять производную по х из выражений,
стоящих слева и справа от знака равенства,
а затем подставить значения
 вместо
х и у. при этом нужно учитывать, что у –
сложная функция и производная от нее
так и останется
вместо
х и у. при этом нужно учитывать, что у –
сложная функция и производная от нее
так и останется
 :
:


Уравнение касательной к графику функций в точке.
Уравнение
касательной имеет вид:
 ,
где
,
где
 ,
,
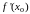 -
значение производной в точке,
-
значение производной в точке,
 ,
,
 - координаты точки касания.
- координаты точки касания.

Алгоритм нахождения уравнения касательной:
Найти , если не дано, подставив в уравнение графика функции, заданной явно.
Найти
 ,
а затем, подставив
и
,
найти
.
,
а затем, подставив
и
,
найти
.Подставить все необходимые значения в формулу касательной.
Пример:
8.30
Напишите
уравнение касательной, проведенной в
точке (1;1) к графику функции
 ,
заданной неявно
,
заданной неявно
 .
.
Решение:
=1 (Из условия).

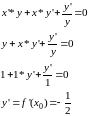
Ответ:
 .
.
Уравнение нормали к графику функций.
Уравнение
нормали к графику функций имеет следующий
вид:
Поэтому алгоритм решения точно такой же как и для касательной.
Пример:
8.36
Напишите
уравнение нормали, проведенной в точке
M(2;1)
к графику функции
,
заданной неявно
 .
.
Решение:
=1
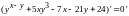
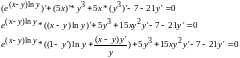


Ответ:

4.3 Производная функции нескольких переменных.
Производная
по переменной берется как обычно, но с
одним отличием: все остальные переменные
считаются константами, т.е. если мы берем
производную по х, то
 и т.д..
и т.д..
Примеры:
Найдите частные производные первого порядка от следующих функций:
13.4.
 .
.
Решение:


13.16. .
.
Решение:
 ;
;
 ;
;
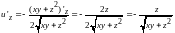 .
.
13.26.
Проверьте,
что функция
 удовлетворяет уравнению
удовлетворяет уравнению
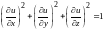 .
.
Решение:


13.39.
Найдите
 и
и
 ,
если
,
если
 и
и
 ,
,
 .
.
Решение:
Для
начала необходимо объяснить разницу
между
и
.
- производная
 ,
с учетом, что все остальные переменные
константы.
=
,
с учетом, что все остальные переменные
константы.
=
 =
= .
Итак:
.
Итак:
= ;
;
=

13.44.
Найдите
производные
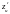 и
и
 функции
функции
 ,
где
,
где
 и
и
 :
: ,
,
 ,
,
 .
.
Решение:
 ;
;
 .
.
13.49.
Найдите
в указанной точке первые частные
производные функции
,
заданной неявно уравнением:
 ,
,
 .
.
Решение:
Аналогично
случаю, когда у нас функция от одной
переменной, берем производную от обеих
частей уравнения сначала по одной
переменной, считая, что z
– сложная функция и ее производная так
и остается
 ,
а затем подставляем значения
,
а затем подставляем значения
 и находим производную. Повторяем с
другими переменными.
и находим производную. Повторяем с
другими переменными.
Для
начала найдем
 ,
подставив в исходное уравнение
,
подставив в исходное уравнение
 :
:

А
теперь найдем
 :
:

А
теперь найдем
 :
:



