
- •Глава I. Аналитическая геометрия………………………………………….……4
- •Карточка.
- •Глава I. Аналитическая геометрия.
- •1.1 Векторы
- •1.2 Прямая и плоскость.
- •1.3 Задачи на нахождение уравнения прямой/плоскости.
- •Делаем чертеж:
- •1.4 Задачи на угол м/у прямыми, плоскостями, прямой и плоскостью.
- •1.5 Задачи на точку пересечения прямых, прямой и плоскости.
- •1.6 Задачи на проекцию.
- •1.7 Задачи на симметрию.
- •Глава II. Матрицы
- •2.1 «Тривиальные» действия
- •2.2Ранг матрицы
- •2.3 Определитель матрицы.
- •2.4 Обратная матрица.
- •2.5 Совместность. Зависимость. Базис
- •2.6 Системы уравнений.
- •2.7 Собственные векторы.
- •Глава III. Пределы.
- •Глава IV. Производные и дифференциалы.
- •4.1 «Тривиальные» производные.
- •4.2 Уравнения касательной и нормали к графику функций.
- •1) Производная в точке, заданная неявно.
- •Уравнение касательной к графику функций в точке.
- •Уравнение нормали к графику функций.
- •4.3 Производная функции нескольких переменных.
- •4.4 Градиент. Производная по направлению.
- •4.5 Первый и второй дифференциал.
- •4.6 Касательная плоскость.
- •4.7 Формулы Тейлора и Маклорена.
- •Глава V. Интегралы.
- •5.1 Свойства интегралов и таблица первообразных.
- •5.2 Метод частичной замены переменной.
- •5.3 Метод замены переменной.
- •5.4 Определенный интеграл.
- •5.5 Двойные интегралы.
- •Глава VI. Точки экстремума функции нескольких переменных.
- •6.1 Локальный экстремум функции.
- •6.2 Локальный условный экстремум.
- •6.3 Метод Лагранжа.
4.4 Градиент. Производная по направлению.
Производная
функция в точке
 функции
функции
 по
направлению
по
направлению
 вычисляется как:
вычисляется как:
 ,
где
,
где
 - градиент функции f
в точке
.
- градиент функции f
в точке
.
Градиент
функции представляет собой вектор,
координатами которого являются значения
производных по х, по у и по другим
переменным (если они есть) в точке, т.е.
 .
.
Пусть
вектор
имеет
координаты
 ,
тогда
,
тогда
 =
= .
.
Кроме
того,
можно записать как
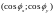 ,
где
,
где
 - косинус угла между вектором
и осью ОХ, а
- косинус угла между вектором
и осью ОХ, а
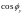 -
косинус угла между вектором
и осью ОУ.
-
косинус угла между вектором
и осью ОУ.
Примеры:
13.56.
Найдите
производную функции
 ,
по направлению
,
по направлению
 в точке
в точке
 .
.
Решение:
 ;
;

 .
.

 .
.
13.57.
Найдите
производную функции
 в точке
в точке
 по направлению
по направлению
 ,
где
,
где
 .
.
Решение:


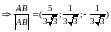 .
.
 .
.
13.60.
Найдите
производную функции
 в точке
в точке
 по направлению луча, образующего с осью
по направлению луча, образующего с осью
 угол
угол
 .
.
Решение:


 .
.
14.10(а)
Найдите
точки, в которых
 если
если


единственная
точка
 .
.
4.5 Первый и второй дифференциал.
Формула
первого дифференциала:

Формула
второго дифференциала:

Примеры:
14.4(а)
Найдите
первый дифференциал функции
Решение:

14.9(а)
Найдите
вторые дифференциалы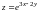
Решение:


 .
.
14.6.
Покажите,
что если
 ,
то
,
то
 .
.
Решение:
Запишем
по-другому, что нам нужно доказать:
 .
А теперь докажем равенство:
.
А теперь докажем равенство:
 .
.
4.6 Касательная плоскость.
Уравнение
касательной плоскости к графику функции
имеет вид:
 ,
кроме того это уравнение можно записать
как:
,
кроме того это уравнение можно записать
как: .
Отсюда можно получить уравнение нормали
к поверхности:
.
Отсюда можно получить уравнение нормали
к поверхности:
 .
.
P.S.
если у нас уравнение задано явно, то мы
считаем, что

Примеры:
14.15.
Напишите
уравнение касательной плоскости и
нормали к поверхности
 в точке
в точке
 .
.
Решение:

 -
уравнение касательной плоскости.
-
уравнение касательной плоскости.
 -
уравнение нормали к поверхности.
-
уравнение нормали к поверхности.
14.21.
Напишите
уравнение касательной плоскости и
нормали к поверхности
 в
точке
в
точке
 .
.
Решение:
Для
начала найдем
 как раньше:
как раньше:
 ;
;
 ;
;


 -
уравнение касательной плоскости
-
уравнение касательной плоскости
 -
уравнение нормали к поверхности.
-
уравнение нормали к поверхности.
4.7 Формулы Тейлора и Маклорена.
Формулы Тейлора и Маклорена для функций одной переменной:
Формула
Тейлора:

Формула
Маклорена:

Формула Тейлора для функций нескольких переменных:
Формула
Тейлора:
 или также можно записать:
или также можно записать:


Глава V. Интегралы.
5.1 Свойства интегралов и таблица первообразных.
Свойства интегралов:




 Стандартная
таблица первообразных:
Стандартная
таблица первообразных:



Расширенная таблица первообразных:

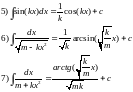
Примерный алгоритм решения интегралов:
Смотрим: если можно решить по таблицам – решаем.
Если нельзя – пробуем метод частичной замены, если можно что-то взять за u – решаем.
Если нельзя – используем метод замены переменной.
P.S. Старайтесь мыслить следующим образом: от чего мне нужно взять производную, чтобы получить подынтегральное выражение?
Примеры:
11.2
 =
=
11.3
 =
=
11.5
 =
=
5.2 Метод частичной замены переменной.
Алгоритм решения:
Мы должны разбить подынтегральное выражение на u и dv. Выбрав, что-то за u, все оставшееся (с dx) считаем за dv.
Приоритет обозначения u:
1
-
 ,
при условии, что они умножается на
выражение, состоящее из х в степени.
,
при условии, что они умножается на
выражение, состоящее из х в степени.
2
– х в степени (встречается чаще всего),
при условии, что умножается на
 и степени положительные.
и степени положительные.
3 - - никогда не берутся за u.
Находим du и v по формулам:
 и
и

Подставляем все известные данные в формулу:

При необходимости повторить.
Примеры:
11.35
 .
.
Решение:
Определяем: u=x, dv=sin(3x)dx
du=1*dx; v=

=

11.42

Решение:
Определяем: u=
 ,
dv=
,
dv=

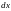
du=2xdx; v=


Повторяем:




 .
.
11.47
 .
.
Решение:
Определяем: u=
 и
и

 ;
;
 .
. =
=
 .
.
