
- •1.Комплексные числа в алгебраической, тригонометрической и показательной
- •2.Многочлены и их делимость. Теорема Безу. Основная теорема алгебры.
- •3. Рациональные дроби и их разложение на сумму простейших дробей. Методы нахождения коэффициентов разложения.
- •4. Первообразная. Неопределенный интеграл и его свойства.
- •9. Интегрирование иррациональных функций.
- •10. Понятие определенного интеграла и его геометрический смысл.
- •11. Свойства определенного интеграла.
- •12. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •13. Замена переменной в определенном интеграле.
- •14. Интегралы от четных, нечетных и периодических функций. Интегрирование по частям в определенном интеграле.
- •15. Вычисление площадей плоских фигур (в т.Ч. Площади фигуры, ограниченной кривой, заданной в параметрическом виде, и площади плоской фигуры в полярной системе координат).
- •16. Вычисление длины дуги с помощью определенного интеграла.
- •18. Несобственные интегралы первого рода, их свойства и вычисление.
- •19. Несобственные интегралы второго рода
- •21. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
- •22. Частные производные
- •23 . Дифференцируемость функции нескольких переменных. Необходимые
- •24. Частные производные сложной функции. Дифференциал сложной функции. Инвариантность формы полного дифференциала.
- •25. Неявные функции и их дифференцирование.
- •26. Геометрический смысл полного дифференциала. Касательная плоскость и
- •27. Частные производные высших порядков. Теорема о равенстве смешанных производных. Дифференциалы высших порядков. Матрица Гессе.
- •28. Формула Тейлора для функции нескольких переменных.
- •29. Локальный экстремум функции нескольких переменных. Необходимое
- •30. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в
- •31. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения
- •32. Криволинейный интеграл первого рода
- •33. Двойной интеграл. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
- •34. Тройной интеграл. Вычисление тройного интеграла в декартовой системе координат. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической и сферической системах координат.
- •Замена переменных в тройном интеграле.
- •35. Поверхностный интеграл первого рода.
- •36. Интегралы по ориентированной фигуре от векторной функции и их свойства.
- •37. Криволинейный интеграл второго рода, его механический смысл, скалярная
- •Скалярная форма кри-2
- •38. Формула Грина.
- •39. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
- •40. Поверхностный интеграл второго рода, его физический смысл, скалярная
- •41. Скалярные поля. Производная скалярного поля по направлению. Градиент.
- •42. Векторные поля. Поток векторного поля. Дивергенция. Формула
- •43. Циркуляция и ротор векторного поля. Формула Стокса. Условия независимости криволинейного интеграла второго рода от пути в пространстве.
- •43. Операторы Гамильтона и Лапласа.
- •45 Потенциальное векторное поле и его свойства.
- •46.Соленоидальное векторное поле. Гармоническое векторное поле.
1.Комплексные числа в алгебраической, тригонометрической и показательной
формах. Действия над комплексными числами, извлечение корня из
комплексного числа. Формула Эйлера.
Число z=x+iy,
где x,y![]()
![]()
![]() называется комплексным числом. Число
i
называется
называется комплексным числом. Число
i
называется
мнимой единицей, x-действительная часть, y-мнимая часть.
Комплексное число z=x-iy называется сопряженным комплексному числу z.
Модулем комплексного
числа z=x+iy
называется |z|=![]()
Представление комплексного числа с помощью формулы z=x+iy называется алгебраической формой комплексного числа.
Тригонометрические
и показательные формы комплексного
числа. Обозначаются через угол
![]() ,
угол между осью OX
и радиус
вектором, изображающим число z.
,
угол между осью OX
и радиус
вектором, изображающим число z.
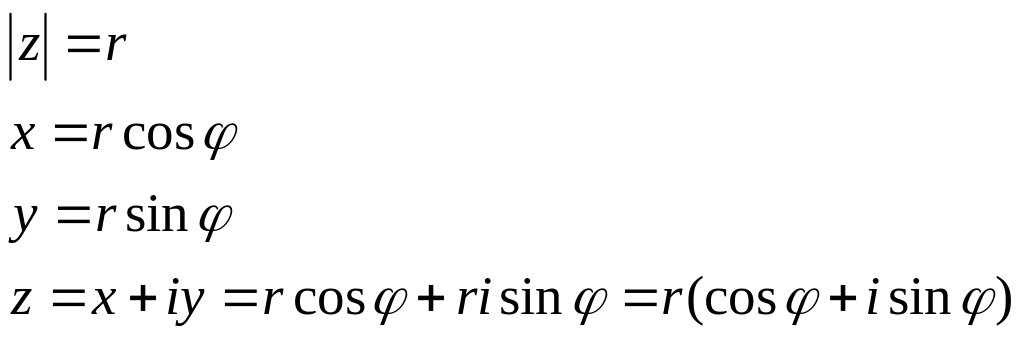
Множество углов
вида
![]() обозначается argz.
обозначается argz.
argz
=
![]()
Представление
комплексного числа формулой
![]() называется
показательной формой комплексного
числа.
называется
показательной формой комплексного
числа.
1.Сложение
![]()
2.Вычитание
![]()
3. Умножение
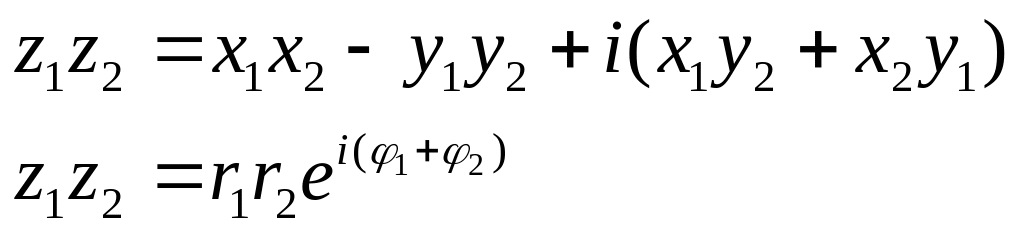
z1*z2 =
r1*r2(cos(![]() 1+
2)
+ isin(
1+
2)
1+
2)
+ isin(
1+
2)
4.Деление
![]()
![]()
![]()
![]() - Формула Муавра
(!)
- Формула Муавра
(!)![]()
![]() -
Формула Эйлера
-
Формула Эйлера
2.Многочлены и их делимость. Теорема Безу. Основная теорема алгебры.
Разложение многочлена на множители. Критерий тождественности двух
многочленов.
Многочлены.
Многочлен (полином)
относительно переменной z
- это![]()
2z4-5z3+2z=(z2-1)(2 z2-5z+2)+(-3z-2)
Qm(z) Tk(z) Rc(z)
Значит Pn(z) = Qm(z) Tk(z) + Rc(z) (*), где m<=n m+k=n, l<n;
Если Rc(z) = 0, то Pn(z) делится на Qm(z).
Назовем компл. число z1 корнем многочл. Pn(z), если Pn(z1).
Теор. БЕЗУ: многочлен не нулевой степени Pn(z) делится на двучлен z-z1, тогда и только тогда, когда z1 является корнем Pn(z).
Запишем (*) для Pn(z) и z-z1: Pn(z) = (z-z1)Tn-1(z)+ Rc(z) => z:=z1.
Основная теорема алгебры(Гаусса): всякий многочлен Pn(z) не нулевой степени имеет по крайней мере 1 комплексный корень.
Компл. число z1 наз. корнем кратности к1 многочл. Pn(z), если
Pn(z) = (z-z1)к1Тn-k1(z)
Следствие: Многочл. Pn(z) имеет n комлексных корней с учетом их кратности:
Pn(z) = an(z-z1)к1(z-z2)к2…
Пусть z1
– корень Pn(z)
с действ. коэф-ми, тогда
![]() корень
Pn(z)
корень
Pn(z)
Pn(
)=![]() =
=![]() =0
=0
Комплексно-сопряж. корни входят в разложение многочлена парами.
(z-z1)(z- )=z2+p1z+q1
Pn(x) – с действ. коэф.
Pn(x)=an(x-x1)k1(x-x2)k2*…*(x-xl)kl(x2+p1x+q1)R1(x2+p2x+q2)R2*…*(x2+pmx+qm)Rm
x1, x2,…,xn – действ. корни
k1, k2,…,kn – их кратности
P1, P2,…,Pn, q1, q2,…,qn – действ. числа
k1+k2+…+kl+2R1+2R2+…+2Rm = n
Два многочлена одинаковой степени тождественно равны друг другу тогда и только тогда, когда равны коэффициенты при одинаковых степенях.
3. Рациональные дроби и их разложение на сумму простейших дробей. Методы нахождения коэффициентов разложения.
Опр.
![]() ,
где Pn(z),
Qm(z)
–
многочлены, наз. рациональной дробью.
,
где Pn(z),
Qm(z)
–
многочлены, наз. рациональной дробью.
n>=m – дробь неправильная; n<m – правильная.
Разложение правильной рац. дроби с комплексными коэф. на сумму простейших дробей.
Если
![]() - правильная дробь, то
- правильная дробь, то
![]() ,
где
,
где
z1, z2,…, zl – разл. компл. корни
k1, k2,…, kl – их кратности
то сущ. Такие компл. числа Aik, где i=1,2,…,l; k=1,2,…,ki, то тогда
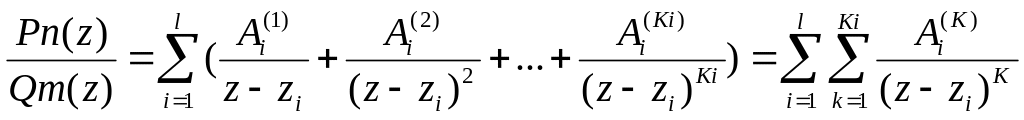
Разложение простой рац. дроби с действ. коэф. на сумму простейших дробей с действ. коэф.
Пусть
- правильная дробь,
![]()
x1, x2,…, xl – разл. компл. корни
k1, k2,…, kl – их кратности
pi2-4qi<0 для i=1…s
R1, R2,…,Rs – кратности пар корней, тогда
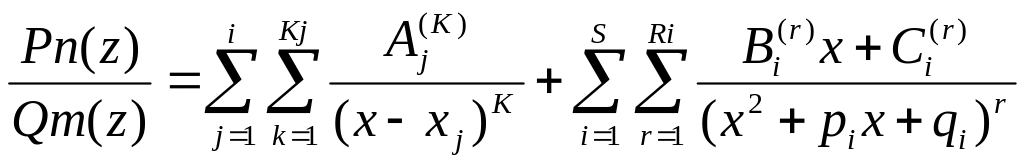
Метод неопределённых коэффициентов.
Метод частных значений.
