
- •1.Комплексные числа в алгебраической, тригонометрической и показательной
- •2.Многочлены и их делимость. Теорема Безу. Основная теорема алгебры.
- •3. Рациональные дроби и их разложение на сумму простейших дробей. Методы нахождения коэффициентов разложения.
- •4. Первообразная. Неопределенный интеграл и его свойства.
- •9. Интегрирование иррациональных функций.
- •10. Понятие определенного интеграла и его геометрический смысл.
- •11. Свойства определенного интеграла.
- •12. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •13. Замена переменной в определенном интеграле.
- •14. Интегралы от четных, нечетных и периодических функций. Интегрирование по частям в определенном интеграле.
- •15. Вычисление площадей плоских фигур (в т.Ч. Площади фигуры, ограниченной кривой, заданной в параметрическом виде, и площади плоской фигуры в полярной системе координат).
- •16. Вычисление длины дуги с помощью определенного интеграла.
- •18. Несобственные интегралы первого рода, их свойства и вычисление.
- •19. Несобственные интегралы второго рода
- •21. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
- •22. Частные производные
- •23 . Дифференцируемость функции нескольких переменных. Необходимые
- •24. Частные производные сложной функции. Дифференциал сложной функции. Инвариантность формы полного дифференциала.
- •25. Неявные функции и их дифференцирование.
- •26. Геометрический смысл полного дифференциала. Касательная плоскость и
- •27. Частные производные высших порядков. Теорема о равенстве смешанных производных. Дифференциалы высших порядков. Матрица Гессе.
- •28. Формула Тейлора для функции нескольких переменных.
- •29. Локальный экстремум функции нескольких переменных. Необходимое
- •30. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в
- •31. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения
- •32. Криволинейный интеграл первого рода
- •33. Двойной интеграл. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
- •34. Тройной интеграл. Вычисление тройного интеграла в декартовой системе координат. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической и сферической системах координат.
- •Замена переменных в тройном интеграле.
- •35. Поверхностный интеграл первого рода.
- •36. Интегралы по ориентированной фигуре от векторной функции и их свойства.
- •37. Криволинейный интеграл второго рода, его механический смысл, скалярная
- •Скалярная форма кри-2
- •38. Формула Грина.
- •39. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
- •40. Поверхностный интеграл второго рода, его физический смысл, скалярная
- •41. Скалярные поля. Производная скалярного поля по направлению. Градиент.
- •42. Векторные поля. Поток векторного поля. Дивергенция. Формула
- •43. Циркуляция и ротор векторного поля. Формула Стокса. Условия независимости криволинейного интеграла второго рода от пути в пространстве.
- •43. Операторы Гамильтона и Лапласа.
- •45 Потенциальное векторное поле и его свойства.
- •46.Соленоидальное векторное поле. Гармоническое векторное поле.
41. Скалярные поля. Производная скалярного поля по направлению. Градиент.
Пусть V
– некоторая область в пространстве.
Говорят, что в этой области задано
скалярное поле, если каждой т.
![]() поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
поставлено
в соответствие некоторое число U(M)
(пример – поле температур, освещенности).
Скалярное поле не зависит от выбора
системы координат. Поверхность или
линия, на которой U(M)
принимает постоянное значение называется
поверхностью уровня скалярного поля.
Пусть U(M)
– некоторое скалярное поле.
![]() -
единственный фиксированный вектор.
-
единственный фиксированный вектор.
![]() -фиксированая
точка.
-фиксированая
точка.
![]() ;
;
![]() ;
;
![]()
Если
![]() ,
то он называется производной скалярного
поля U(M)
по направлению
,
то он называется производной скалярного
поля U(M)
по направлению
![]() в точке
.
в точке
.
![]()
lnH-скорость изменения ф-ции U(m) по направлению в точке .
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() принимает наибольшее
значение при
принимает наибольшее
значение при
![]() ,
т.е. в направлении вектора gradU
в т.
,
т.е. в направлении вектора gradU
в т.
gradU указывает направление наибольшего роста поля в данной точке. | gradU| - скорость роста ф-ции U в данном направлении. Вектро gradU не зависит от выбора системы координат. Grad направлен по поверхности уровня в данной точке.
42. Векторные поля. Поток векторного поля. Дивергенция. Формула
Остроградского.
Векторные поля и их основные характеристики.
Говорят, что в V
занадо векторное поле, если каждой т.
поставлен
в соответствие некоторый вектор
.
Физ. Векторные поля не зависят от выбора
СК.
![]()
Векторная линия – кривая, в каждой точке M которой направлен по касательной к кривой. Векторная трубка – часть пространства, состоящая из целых векторных линий, каждая ВЛ или целиком лежит внутри этой трубки или находится вне ее.
Поток векторного поля. Дивергенция.
![]()
Дивиргенцией
векторного поля
![]() называется
скалярная ф-ция
называется
скалярная ф-ция
![]() .
.
Формула Остроградского:
![]()
![]() характеризует
плотность источников поля в данной
точке. Не зависит от выбора СК.
характеризует
плотность источников поля в данной
точке. Не зависит от выбора СК.
Циркуляция и ротор векторного поля.
Ротором (или вихрем)
векторного поля
называется вектор-функция

Ротор характеризует завихренность поля в данной точке.
Ротор является постоянным вектором, направленным вдоль оси вращения OZ. Его модуль равен удвоенной угловой скорости вращения тела.
Рассмотрим
.
С- кусочно гладкая пов-ть. КРИ-2
![]() называется циркуляцией
называется циркуляцией
![]() вдоль кривой L
в направлении
вдоль кривой L
в направлении
![]() .
Если
-силовое
поле, то его циркуляция – работа вдоль
пути L.
.
Если
-силовое
поле, то его циркуляция – работа вдоль
пути L.
![]()
(формула Стокса).
43. Циркуляция и ротор векторного поля. Формула Стокса. Условия независимости криволинейного интеграла второго рода от пути в пространстве.
Ротором (или вихрем) векторного поля называется вектор-функция
Ротор характеризует завихренность поля в данной точке.
Ротор является постоянным вектором, направленным вдоль оси вращения OZ. Его модуль равен удвоенной угловой скорости вращения тела.
Рассмотрим . С- кусочно гладкая пов-ть. КРИ-2 называется
циркуляцией вдоль кривой L в направлении . Если -силовое поле, то его циркуляция – работа вдоль пути L.
(формула Стокса).
43. Операторы Гамильтона и Лапласа.
Опера́тор Лапла́са (Лапласиан) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом Δ. Функции F он ставит в соответствие функцию

В сферических координатах:

или
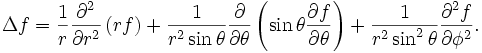
Оператор Лапласа часто записывается следующим образом , то есть скалярное произведение оператора набла на себя.
Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом (набла) Под этим оператором подразумевается вектор с компонентами
![]()
в n-мерном пространстве.
Для трёхмерного декартового пространства оператор набла определяется следующим образом
![]() Свойства оператора
набла
Свойства оператора
набла
Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, на которую он умножается.
Если умножить вектор набла а скаляр φ, то получится вектор
![]() который представляет
собой градиент функции φ.
который представляет
собой градиент функции φ.
Если вектор набла скалярно умножить на вектор , получится скаляр:
![]() то есть дивергенция
вектора
то есть дивергенция
вектора
![]() .
.
Если
![]() умножить на
векторно, то получится ротор вектора
.
умножить на
векторно, то получится ротор вектора
.
Также, произведение
![]() есть оператор Лапласа, и обозначается
Δ. В декартовых координатах оператор
Лапласа определяется следующим образом:
есть оператор Лапласа, и обозначается
Δ. В декартовых координатах оператор
Лапласа определяется следующим образом:

Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:
![]()
![]()
