
- •1.Комплексные числа в алгебраической, тригонометрической и показательной
- •2.Многочлены и их делимость. Теорема Безу. Основная теорема алгебры.
- •3. Рациональные дроби и их разложение на сумму простейших дробей. Методы нахождения коэффициентов разложения.
- •4. Первообразная. Неопределенный интеграл и его свойства.
- •9. Интегрирование иррациональных функций.
- •10. Понятие определенного интеграла и его геометрический смысл.
- •11. Свойства определенного интеграла.
- •12. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •13. Замена переменной в определенном интеграле.
- •14. Интегралы от четных, нечетных и периодических функций. Интегрирование по частям в определенном интеграле.
- •15. Вычисление площадей плоских фигур (в т.Ч. Площади фигуры, ограниченной кривой, заданной в параметрическом виде, и площади плоской фигуры в полярной системе координат).
- •16. Вычисление длины дуги с помощью определенного интеграла.
- •18. Несобственные интегралы первого рода, их свойства и вычисление.
- •19. Несобственные интегралы второго рода
- •21. Понятие функции нескольких переменных. Предел функции нескольких переменных в точке, повторные пределы. Непрерывность.
- •22. Частные производные
- •23 . Дифференцируемость функции нескольких переменных. Необходимые
- •24. Частные производные сложной функции. Дифференциал сложной функции. Инвариантность формы полного дифференциала.
- •25. Неявные функции и их дифференцирование.
- •26. Геометрический смысл полного дифференциала. Касательная плоскость и
- •27. Частные производные высших порядков. Теорема о равенстве смешанных производных. Дифференциалы высших порядков. Матрица Гессе.
- •28. Формула Тейлора для функции нескольких переменных.
- •29. Локальный экстремум функции нескольких переменных. Необходимое
- •30. Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в
- •31. Интегралы по фигуре от скалярной функции, их свойства, геометрические и физические приложения
- •32. Криволинейный интеграл первого рода
- •33. Двойной интеграл. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
- •34. Тройной интеграл. Вычисление тройного интеграла в декартовой системе координат. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической и сферической системах координат.
- •Замена переменных в тройном интеграле.
- •35. Поверхностный интеграл первого рода.
- •36. Интегралы по ориентированной фигуре от векторной функции и их свойства.
- •37. Криволинейный интеграл второго рода, его механический смысл, скалярная
- •Скалярная форма кри-2
- •38. Формула Грина.
- •39. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
- •40. Поверхностный интеграл второго рода, его физический смысл, скалярная
- •41. Скалярные поля. Производная скалярного поля по направлению. Градиент.
- •42. Векторные поля. Поток векторного поля. Дивергенция. Формула
- •43. Циркуляция и ротор векторного поля. Формула Стокса. Условия независимости криволинейного интеграла второго рода от пути в пространстве.
- •43. Операторы Гамильтона и Лапласа.
- •45 Потенциальное векторное поле и его свойства.
- •46.Соленоидальное векторное поле. Гармоническое векторное поле.
32. Криволинейный интеграл первого рода
Криволинейный интеграл 1го рода.
![]() 1).
1).
![]() ;
;
![]() - диф-ма на [a,b];
- диф-ма на [a,b];
![]()
![]() ;
L:
x=g(y);
;
L:
x=g(y);
![]()
![]() ;
;
2).
![]() ;
x(t),y(t)
– непрерывно диф-ма на
;
x(t),y(t)
– непрерывно диф-ма на
![]() ;
L:
;
L:
![]()
![]() ;
;
3).
![]() ;
;![]() ;
L:
;
L:
![]()

4).
;
![]() ;L:
;L:
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
33. Двойной интеграл. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.
Двойной интеграл, его вычисление в декартовой прямоугольной системе координат.
![]() ;
;
![]() ;
;
y-трапецевидная
область Д.
![]()
x-трапецевидная
область Д
![]()
Пусть в основании цилиндрического тела лежит y-трапецевидная область.
![]() ;
;
 ;
;
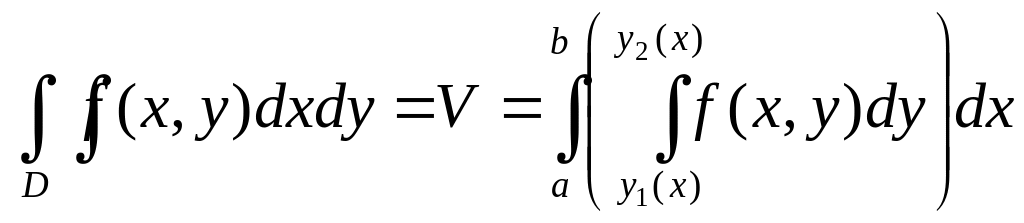
 для y-трапецевидной
области
для y-трапецевидной
области
 для x-трапецевидной
области
для x-трапецевидной
области
Замечание: области более сложного вида разбиваются на сумму трапецевидных областей.
Замена переменной в двойном интеграле.
![]() (
(
 *)
*)
Свойства
x(u,v), y(u,v) – взаимно однозначны
x(u,v), y(u,v) – непрерывные, непр. частн. пр-е 1-го порядка

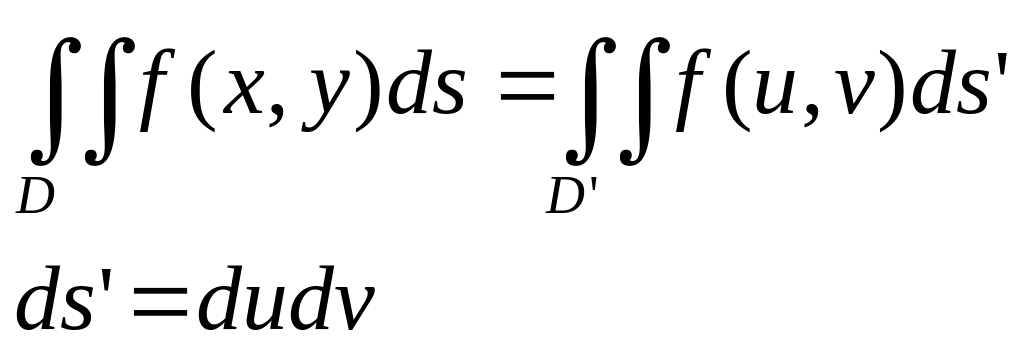
![]()
P1: x(u,v), y(u,v)
P2: x(u+∆u,v), y(u+∆u,v)
![]()
![]()
![]()

![]()
I – Якобиан(Якоби)
Модуль I – коэффициет растяжения площади в т. с координатами u и v при отображении D на D’.
![]()
Вычисление в полярной сист координат.
,
![]()
![]()

a)

b )
)
![]()

c)
![]()
34. Тройной интеграл. Вычисление тройного интеграла в декартовой системе координат. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрической и сферической системах координат.
Тройной интеграл.
![]() :
:
 ,
z
меняется от поверхности до поверхности.
,
z
меняется от поверхности до поверхности.
Замечание: Области более сложного вида надо разбить на области более простого вида. Проектирование области V можно производить и на другую плоскость.
Замена переменных в тройном интеграле.
![]() ,
где |I|
- модуль Якобина.
,
где |I|
- модуль Якобина.
 Геометрический
смысл: |I|
-коэффициент растяжения объёма при
отображении области V
на область V’
Геометрический
смысл: |I|
-коэффициент растяжения объёма при
отображении области V
на область V’
В цилиндрических координатах:
![]()
В сферических координатах:

35. Поверхностный интеграл первого рода.
Поверхностный интеграл1-го рода (ПОВИ-1).
![]() ,
,
![]() -гладкая(в
каждой точке существует касательная
плоскость). Пусть
такова, что прямая параллельная OZ
пересекает её не более чем в 1-ой точке.
Тогда z=f(x,y);
-гладкая(в
каждой точке существует касательная
плоскость). Пусть
такова, что прямая параллельная OZ
пересекает её не более чем в 1-ой точке.
Тогда z=f(x,y);
![]() ;
;

Примечание: Можно проецировать и не на поверхность XOY. Например: x= (y,z);
36. Интегралы по ориентированной фигуре от векторной функции и их свойства.
Интеграл по ориентированной фигуре от векторной ф-ции.
![]()
Векторная
ф-ция 3х переменных x,y,z,
определенной на фигуре Ф. Ф-ции P,Q,R
называются координатами
![]() .
Фигура Ф называется ориентированной,
если в каждой ее точке М задан некоторый
вектор
.
Фигура Ф называется ориентированной,
если в каждой ее точке М задан некоторый
вектор
![]() ,
характеризующий эту фигуру. Диния
,
характеризующий эту фигуру. Диния
![]() называется ориентированной, если на
ней выбрано направление перемещения.
называется ориентированной, если на
ней выбрано направление перемещения.
Гладкая поверхность называется двусторонняя, если нормаль к ней при обходе по замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, возвращается к своему первоначальному положению.
1).
;
2).
![]() ;
3).
;
3).
![]() ; 4).
; 4).
![]()
5).
![]() ; n-я
интегральная сумма для векторной ф-ции
a(M)
по ориентированной с помощью вектора
P(n)
фигуре Ф. ; 6).
; n-я
интегральная сумма для векторной ф-ции
a(M)
по ориентированной с помощью вектора
P(n)
фигуре Ф. ; 6).
![]() (*)
(*)
Если (*) существует, конечен и не зависит от способа построения интегральной суммы , то он называется интегралом по орентированной фигуре Ф от векторной ф-ции a(M).
![]()
![]()
P(x,y,z) Q(x,y,z) R(x,y,z) a=(P,Q,R)
Если ф-ции P,Q,R непрерывны на гладкой, ограниченной, содержащей граничные точки ориентированной фигуре Ф, то интеграл существует.
Частные случаи интегралов по ориентированной фигуре.
Свойства интеграла по фигуре от векторной ф-ции.
1).
![]() ;
2).
;
2).
![]() ,
c=const
,
c=const
3).
![]() ; 4).
; 4).
![]()
