Задачи и содержание работы по изучению элементов наглядной геометрии.

Основные задачи изучения геометрического материала в 1-4 классах заключаются в том, чтобы создать у детей четкие и правильные геометрические образы, развить пространственные представления, вооружить их навыками черчения и измерения, имеющими большое жизненно – практическое значение, и тем самым подготовить учеников к успешному изучению систематического курса геометрии.

В содержании начального геометрического образования должны найти свое отражение – пусть в самой элементарной и доступной детям форме – основные геометрические идеи – движения преобразования, инвариантности основных свойств геометрических фигур. Уже на первой ступени приобщения к геометрическим знаниям дети должны получить первоначальную ориентировку во взаимном расположении фигур, в умении выделять изучаемые фигуры как элементы тел. Арифметические и геометрические знания должны тесно сочетаться и находиться в органическом единстве.

В соответствии с программой начальных классов дети знакомятся с прямой линией, отрезком, измерением и вычерчиванием отрезков, с их разностным и кратким сравнением, с углами (прямой, тупой, острый), с прямоугольником, квадратом и их свойствами, с вычислениями их периметров и площадей, с геометрическими телами: кубом и прямоугольным параллелепипедом; с их некоторыми свойствами, с вычислением их объемов. Программой предусмотрено провешивание и измерение прямой линии, проведение измерительных работ на местности.

2. Особенности восприятия:

В осприятие – это психический процесс, позволяющий отражать предметы, явления в целом. Ещё в дошкольном возраст учащиеся учат различать и , и , поэтому в начальной школе необходимо сформировать у учащихся способность выявлять существенные признаки геометрических объектов и способность различать их друг от друга, квадрат от прямоугольника, плоскую фигуру от объёмной, так же находить общие признаки.

Особенности восприятия таковы, что:

1. Опредмечивание незнакомых форм

куб – кубик, конус – пирамида, шар – мячик. Правильность обозначения фигур 55 %

2. Плоскостные знают лучше чем объёмные, и путают объёмные тела с плоскими формами.

круг – шарик

3. «Привязаны» к определенному распространению фигуры на плоскости.

Методические приёмы, с учётом особенностей восприятия:

1. различное расположение фигур на плоскости

отрезки

квадраты

углы

2. Вылепливание и разрезание объёмных фигур

3. Изготовление развёрток объёмных фигур

4. Классификация

3. Варианты игры.

• Загадывание фигуры и ответы на вопросы

• Уберите лишнюю фигуру

• Дана геометрическая фигура, придумайте предметы с этой геометрической фигурой, встречающиеся в жизн

• Нарисуй что хочешь. Составь геометрическое описание своего рисунка.

• Надень волшебные очки, через которые мы видим всё вокруг нас только в виде треугольников (квадратов и т.д.), нарисуй, что у тебя получилось.

• Дорисуй так, чтобы получился какой-то предмет. Игра «Давай пофантазируем». Даются различные фигуры или несколько фигур. 

Игра «Внимание»

• Сколько на рисунке треугольников? (других геометрических фигур?).

• Чем отличаются картинки?

• Раскрась участки, на которых ты встретишь такие фигуры (даются образцы различных фигур и большой рисунок, который составляют эти фигуры). 

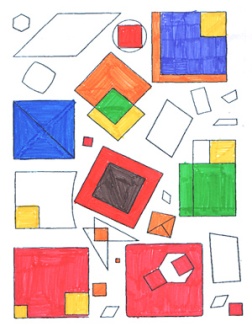
• Продолжи линию, Дорисуй рисунки, чтобы они были одинаковыми и т.д.

20.

1. Деятельность, которую выполняют учащиеся в процессе обучения, может быть репродуктивной и продуктивной. Репродуктивная деятельность характеризуется тем, что ученик получает готовую информацию, воспринимает её, понимает, запоминает, затем воспроизводит. Продуктивная деятельность связана с активной работой мышления, и находит своё отражение в таких мыслительных операциях, как анализ и синтез, сравнение, классификация, аналогия, обобщение. Эти мыслительные операции в психолого – педагогической литературе принято называть логическими приёмами мышления или приёмами умственных действий. Включение этих операций в процесс усвоения математического содержания – одно из важных условий построения развивающего обучения, так как продуктивная деятельность оказывает положительное влияние на развитие всех психических функции «… организация развивающего обучения предполагает создание условий для овладения школьниками приёмами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но даёт существенные сдвиги в умственном развитии ребенка. Овладев этими приёмами, ученики становятся более самостоятельными в решении учебных задач, могут рационально строить свою деятельность по усвоению знаний».

Анализ и синтез.

Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое. Способность к аналитико – синтетической деятельности находит своё выражение не только в умении выделять элементы того или иного объекта, его различные признаки или соединять элементы в единое целое, но и в умении включать их в новые связи, увидеть их новые функции.

Формированию этих умений может способствовать:

1. рассмотрение данного объекта с точки зрения различных понятий;

2. постановка различных заданий к данному математическому объекту

Для первого предлагают такие задания: Прочитайте по - разному выражения 16 – 5 (16 уменьшили на 5 или разность чисел 16 и 5 или из 16 вычесть 5).

1) по каким признакам можно разложить пуговицы в 2 коробки?

2) Разгадайте правило, по которому составлена таблица и дополни данные.

3)Сколько отрезков на чертеже? Сколько треугольников? Сколько многоугольников?

Для второго: По какому правилу записан первый ряд? Разбейте числа на две группы, так, чтобы в них были похожие между собой? Какая пара лишняя?

Приём сравнения.

Формирование умения пользоваться этим приёмом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания. Целесообразно, например, ориентироваться на такие этапы:

• Выделение признаков или свойств одного предмета;

• Установление сходства и различия между признаками двух объектов;

• Выявление сходства между признаками трёх, четырёх и более объектов.

Так как работу по формированию у детей логического приёма сравнения лучше начать с первых уроков математики, то в качестве объектов можно сначала использовать предметы или рисунки с изображением предметов, хорошо им знакомых, в которых они могут выделить те или иные признаки, опираясь на имеющиеся у них представления.

Для организации деятельности учащихся, направленной на выделение признаков того или иного объекта, можно сначала предложить такой вопрос:

- Что вы можете рассказать о предмете?

В процессе работы учитель знакомит детей с понятиями «размер», «форма» и предлагает им следующие вопросы: Что вы можете сказать о размерах предметов?

Для выявления признаков или свойств какого-то предмета учитель обычно обращается к детям с вопросами:

-В чём сходство и различие этих объектов?

-Что изменилось?

Возможно, познакомить их с термином «признак» и использовать его при выполнении задания: «Назови признаки предмета или Назови сходные и различные признаки предметов».

Умение выделять признаки и, ориентируясь на них, сравнивать предметы ученики переносят на математические объекты.

Назовите признаки:

выражения 3+2 (числа 3,2 и знак «+»)

выражения 6 – 1 ( числа 6,1 и знак «-»)

Приём сравнения можно использовать при знакомстве учеников с новыми понятиями

Чем похожи между собой все:

1) числа 50,60,70,80 (разрядные десятки);

2) геометрические фигуры (четырёхугольники);

Показатель сформированности приёма сравнения – умение детей самостоятельно использовать его для решения различных задач, без указания «сравни..., укажи признаки.., в чём сходство и развитие…»

Приём классификации.

Умение выделять признаки предметов и устанавливать между ними сходство и различие – основа приёма классификации. Из курса математики известно, что при разбиении множества на классы необходимо выполнять следующие условия:

1. ни одно из подмножеств не пусто;

2. подмножества попарно не пересекаются;

3. объединение всех подмножеств составляет данное множество;

Предлагая детям задание на классификацию, эти условия необходимо учитывать.

Умение выполнять классификацию формируется у школьников в тесной связи с изучением конкретного содержания. Например, для упражнений в счёте им часто предлагаются иллюстрации, к которым можно подставить вопросы, начинающиеся со слова «Сколько…?»

-Сколько больших кругов? Сколько маленьких? Красных? Синих? Больших красных? Маленьких синих?

Упражняясь в счёте, учащиеся овладевают логическим приёмом классификации. Задания, связанные с приёмом классификации, обычно формулируются в таком виде: «Разбейте все круги на две группы по какому – то признаку».

Приём аналогии.

Понятие «аналогичный» в переводе с греческого языка означает «сходный», «соответственный», понятие аналогия – сходство в каком –либо отношении между предметами, явлениями, понятиями, способами действий.

Формируя у младших школьников умение, выполнять умозаключения по аналогии, необходимо иметь в виду следующее:

• Аналогия основывается на сравнении, поэтому успех её применения зависит от того, насколько ученики умеют выделять признаки объектов и устанавливать сходство и различие между ними

• Для использования аналогии необходимо иметь два объекта, один из которых известен, второй сравнивается с ним по каким – либо признакам.

• Для ориентации школьников на использование приёма аналогии необходимо в доступной форме разъяснить им суть приёма, обратив их внимание на то, что в математике нередко новый способ действий можно открыть по догадке, вспомнив и проанализировав известный способ действий и данное новое задание.

• Для правильных действий по аналогии сравниваются признаки объектов, существенные в данной ситуации.

Приём обобщение.

Выделение существенных признаков математических объектов, их свойств и отношений – основная характеристика такого приёма умственных действий, как обобщение.

Следует различать результат и процесс обобщения. Результат фиксируется в понятиях, суждениях, правилах. Процесс же обобщения может быть организован по – разному. В зависимости от этого говорят о двух типах обобщения – теоретическом и эмпирическом.

В курсе начальной математики наиболее часто применяется эмпирический тип, при котором обобщение значения является результатом индуктивных рассуждений.

Для получения правильного обобщения индуктивным способом необходимо:

1. продумать подбор математических объектов и последовательность вопросов для целенаправленного наблюдения и сравнения;

2. рассмотреть как можно больше частных объектов, в которых повторяется та закономерность, которую ученики должны подметить;

3. варьировать виды частных объектов, т. е. использовать предметные ситуации, схемы таблицы, выражения;

4. помогать детям словесно формулировать свои наблюдения, задавая наводящие вопросы, уточняя и корректируя те формулировки, которые они предлагают.

2.

3+2 4+2 3+6 4+5 5+3

2+3 2+4 6+3 5+4 3+5

Выясняется, чем похожи и чем отличаются равенства в каждом столбике. Ответы могут быть такими: «Слагаемые одинаковые, они переставлены», «Суммы одинаковые», «Слагаемые одинаковые, они переставлены, суммы одинаковые». Учитель помогает с помощью наводящего вопроса формулировать свойство: «Если слагаемые переставить, то что можно сказать о сумме?»

Вывод: « Если слагаемые переставить, то сумма не изменится» или «От перестановки мест слагаемых сумма не меняется».

3. Индукция (лат. inductio — наведение) — процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления.^[1]

Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.

Различают полную индукцию — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности, и неполную индукцию — наблюдения за отдельными частными случаями наводят на гипотезу, которая, конечно, нуждается в доказательстве. Также для доказательств используется метод математической индукции.

При изучении этой темы необходимо обеспечить усвоение детьми рациональных вычислительных приемов сложения в пределах первого десятка; сформировать прочные вычислительные навыки; добиться запоминания наизусть результатов сложения, а также состава чисел из слагаемых. С переместительным свойством сложения можно ознакомить детей так. Учащимся предлагают, например, положить 4 синих треугольника и придвинуть к ним 3 красных треугольника. Сколько всего треугольников? Как узнать? (Записывают 4+3=7) Затем дается задание поменять местами синие и красные треугольники и к трем красным треугольникам придвинуть четыре синих треугольников. Записывают, какой пример теперь решили (3+4=7). Читаю оба примера с названием чисел при сложении. Сравнивают примеры, т.е. находят, чем примеры отличаются и чем они похожи (слагаемые переставлены, их поменяли местами, а сумма получилась одинакова). Затем показывают. Как использовать прием перестановки при решении примеров и задач на сложение в пределах 10. В процессе упражнений у детей формируется умение применять прием перестановки слагаемых. После этого составляется краткая таблица сложения в пределах 10, зная которую можно решать все примеры на сложение в пределах первого десятка:

2+2=4

3+2=5

4+2=6

5+2=7 и т.д.

 Материал многочисленных наблюдений учитель должен использовать для посильных детям обобщений, которые помогают рационально выполнять вычисления. Так, наблюдая и сравнивая пары примеров вида 4+5, 5+4, дети приходят к выводу, что сумма не зависит от порядка, в котором складываются числа, и используют это свойство сложения, когда к меньшему числу нужно прибавить большее.

 В результате изученной темы ученики должны знать:

1. Сознательное усвоение детьми того, что, если при сложении двух чисел поменять их местами, то результат от этого не изменится.

2. Понимание того, что прием перестановки чисел при сложении облегчает вычисление в тех случаях, когда к меньшему числу прибавить большее.

3. Формирование у детей умений применять в практике вычислений не только рассматривавшийся ранее прием прибавления числа по частям, но и, когда это целесообразно, прием перестановки слагаемых.

 Задания.

1. Учитель берет в одну руку 3 карандаша, а в другую - 5. (Дети делают запись:3+5) А затем учитель скрещивает руки. (Дети записывают 5+3) Как можно узнать, сколько всего карандашей? (8)Сравните записи. Чем они отличаются? Почему получился один и тот же ответ? (складывали те же самые числа, только переставляли их)

2 . Чем похожи фишки домино, чем отличаются?

   

 

3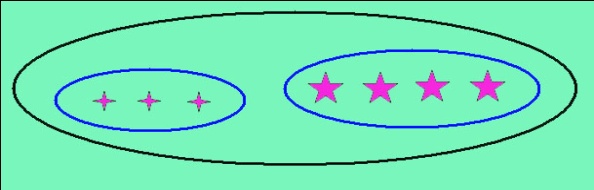 . Выбери равенство, которые соответствуют рисунку.

4+3=7 5+2=7 1+6=7 3+4=7

4. Вставь пропущенные числа:

3+5=…+3 4+2=…+4 2+1=1+… 5+1=1+… 6+2=2+…

5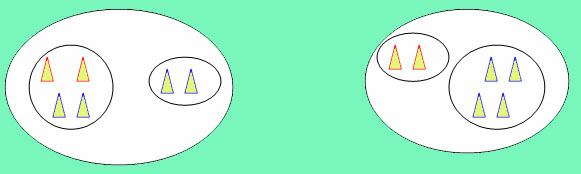 . Выбери равенства, которые соответствуют данным рисункам. Объясни, что обозначает каждое число в этих равенствах. ;

3+2=5 4+2=6 2+4=6

5+1=6 3+3=6 4+1=5

6. Догадайся! По какому правилу таблица?

Запомни пустые клетки и запиши верные равенства.

 7. Можно ли утверждать, что значения выражений в каждом столбике одинаковы?

а) 1+2+2+1

1+4+1

1+2+3

1+5;

б) 2+1+1+1

2+2+1

2+1+2

2+3;

в) 2+1+1+1+1

2+2+1+1

2+3+1

2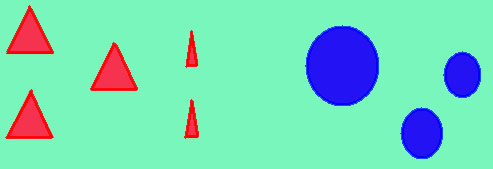 +4.

8. По каким признакам можно разбить все фигуры на две группы?

Выполни рисунки, которые соответствуют равенствам 4+4=8; 6+2=8

 9. Чем похожи рисунки?

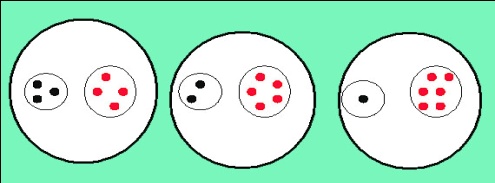
 Какому рисунку соответствует каждое равенство.

6+1=7

5+2=7

3+4=7

1+6=7

2+5=7

4+3=7?

1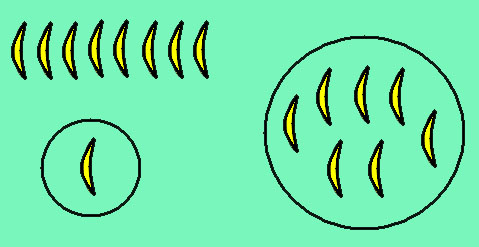 0. Как разложить 8 бананов на 2 тарелки?

Объясни, что обозначает данное равенство:1+7=8.

Можно ли разложить 7 огурцов на 2 тарелки по-другому?

25. Различные методические подходы к формированию умения решать задачи. Вопрос о том, как научить детей устанавливать связи между данными и искомыми в текстовой задаче и в соответствии с этим выбрать, а затем выполнить арифметические действия, решается в методической науке по-разному.

Тем не менее, все многообразие методических рекомендаций, связанных с обучением младших школьников решению задач, целесообразно рассматривать с точки зрения двух принципиально отличающихся друг от друга подходов.

Один подход нацелен на формирование у учащихся умения решать задачи определенных типов (некоторые методисты употребляют термин «видов»).

При одном походе дети сначала учатся решать простые задачи, а затем составные, включающие в себя различные сочетания простых задач.

Процесс обучения решению простых задач является одновременно процессом формирования математических понятий. В связи с этим, в зависимости от тех понятий, которые рассматриваются в курсе математики начальных классов, простые задачи делятся на три группы:

• первая группа включает простые задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий (сложение, вычитание, умножение, деление);

• вторая группа включает простые задачи, при решении которых учащиеся усваивают связь между компонентами и результатами арифметических действий. Это простые задачи на нахождение неизвестного компонента (8 видов);

• третья группа - простые задачи, при решении которых раскрываются понятия разностного сравнения (6 видов) и кратного отношения (6 видов);

Научить детей решать задачи — значит, научить их устанавливать связи между данными и искомым и в соответствии с этим выбирать, а затем и выполнять арифметические действия.

Центральным звеном в умении решать задачи, которым должны овладеть учащиеся, является усвоение связей между данными и искомым. От того, насколько хорошо усвоены учащимися эти связи, зависит их умение решать задачи. Учитывая это, в начальных классах ведется работа над группами задач, решение которых основывается на одних и тех же связях между данными и искомым, а отличаются они конкретным содержанием и числовыми данными. Группы таких задач будем называть задачами одного вида. Работа над задачами не должна сводиться к натаскиванию учащихся на решение задач сначала одного вида, затем другого и т. д. Главная ее цель — научить детей осознанно устанавливать определенные связи между данными и искомым в разных жизненных ситуациях, предусматривая постепенное их усложнение. Чтобы добиться этого, учитель должен предусмотреть в методике обучения решению задач каждого вида такие ступени:

1)подготовительную работу к решению задач;

2)ознакомление с решением задач;

3)закрепление умения решать задачи.

Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к расчленению ее на ряд простых задач и к последовательному их решению. Таким образом, для решения составной задачи надо установить систему связей между данными и искомым, в соответствии с которой выбрать, а затем выполнить арифметические действия.

 Методика работы с каждым новым видом составных задач, согласно данному подходу, ведется также в соответствии с тремя ступенями: подготовительная, ознакомительная, закрепление. Процесс решения каждой составной задачи осуществляется поэтапно:

1.Ознакомление с содержанием задачи.

2.Поиск решения задачи.

3.Составление плана решения.

4.Запись решения и ответа.

5.Проверка решения задачи.

Сначала задачу читает учитель или кто-то из учеников (первое прочтение). Затем учащимся предлагается прочитать задачу про себя, так как не все могут сосредоточиться на ее содержании, когда один из учеников читает вслух (второе прочтение).

-Кто может повторить задачу? (Дети воспроизводят текст по памяти - третье прочтение).

-Выделите условие и вопрос задачи (четвертое прочтении). Фактически опять воспроизводится текст.

-Что нам известно? (пятое прочтение, ученики воспроизводит условие).

-Что неизвестно? (Воспроизводится вопрос.)

Как видно, действия школьников сводятся к тому, что они пять раз воспроизводят текст: сначала читают вслух, затем про себя, потом по частям (условие и вопрос), выделяют известное и неизвестное.

Результатом этой работы, должно явиться осознание текста, т.е. представление той ситуации, которая нашла в нем отражение. Но практика показывает, что многократное воспроизведение текст задачи не всегда эффективно для его осознания. Ученики читают задачу, воспроизводят ее, выделяют условие и вопрос, утвердительно отвечают на вопрос: «Понял ли ты задачу?», но самостоятельно приступить к ее решению не могут.

В этом случае учитель пытается помочь детям, дополняя фронтальную беседу выполнением краткой записи.

Используя такую запись, он организует целенаправленный поиск решения, применяя один из способов разбора задачи: синтетический или аналитический.

Используя при решении каждой задачи аналитический или синтетический способ разбора, учитель в конечном итоге добивается, что дети сами задают себе эти вопросы в определенной последовательности и выполняют рассуждения, связанные с решением задачи.

Основным методом обучения решению составных задач при этом подходе является показ способов решения определенных видов задач и значительная, порой изнурительная практика по овладению ими, т.е. используется объяснительно-иллюстративный и репродуктивный методы обучения (классификация И.Я. Лернера - М.Н.Cкаткина). Поэтому многие учащиеся решают задачи лишь по образцу.

Цель другого подхода, (по мнению его сторонников: Истоминой Н.Б., Фридмана Л.М., Александровой Э.А., Аргинской И.И. и др.) - научить детей выполнять семантический, логический и математический анализ текстовых задач, выявлять взаимосвязи между условием и вопросом, данными и искомыми и представлять эти связи в виде схематических и символических моделей.

Процесс решения задач (простых и составных) рассматривается как переход от словесной модели к модели математической или схематической. В основе осуществления этого перехода лежит семантический анализ текста (установление особенности словесной формулировки этих задач, выявление, какими языковыми средствами выражаются в них отдельные элементы, как можно на основе анализа словесной формулировки задачи распознать отдельные значения величин и их виды, а так же соотношения, связывающие значения величин и т.д.) [15, 89] и выделение в нем математических понятий и отношений (математический анализ текста). Естественно, учащиеся должны быть подготовлены к этой деятельности. Отсюда следует, что знакомству младших школьников с текстовой задачей должна предшествовать специальная работа по формированию математических понятий и отношений, которые они будут использовать при решении текстовых задач. Так как процесс решения задач связан с выделением посылок и построением умозаключений, необходимо также сформировать у младших школьников (до знакомства с задачей) те логические приемы мышления (анализ и синтез, сравнение, обобщение), которые обеспечивали бы их мыслительную деятельность в процессе решения задач.

Таким образом, готовность школьников к знакомству с текстовой задачей предполагает сформированность:

1)   умения описывать предметные ситуации и переводить их на язык схем и математических символов;

2)   представлений о смысле действий сложения и вычитания, и взаимосвязи;

3)   понятий «увеличить (уменьшить) на», разностного сравнения;

4)   навыков чтения;

5)   умения переводить текстовые ситуации в предметные и схематические модели и обратно и др.

Именно второй подход позволяет в большей степени формировать общее умение решать текстовые задачи.

Чтобы научить ребёнка решать текстовые задачи, учитель должен в разумном сочетании использовать оба подхода. А всё многообразие методических рекомендаций, связанных с обучением младших школьников решению задач, целесообразно рассматривать преимущественно с точки зрения второго подхода.

2.