
- •Свойства определителей
- •Алгоритм вычисления обратной матрицы.
- •Элементарные преобразования матрицы:
- •Метод обратной матрицы.
- •Условие совместимости линейных уравнений. Теоремы о числе решений (без доказательств).
- •14. Методы Гаусса решения слау.
- •Пример. Методом Гаусса решить систему:
- •15. Однородные системы линейных уравнений.
- •16. Виды числовых множеств.
- •17. Понятия отображения и функции. Способы задания функции.
- •Понятие функции одной переменной
- •Способы задания функций:
- •Понятие функции одной переменной
- •Способы задания функций:
- •19. Понятия абсолютной величины. Свойства.
- •20. Монотонные и ограниченные функции. Четные и нечетные. Периодические функции. Сложная и обратная функции.
- •21. Предел функции х→∞и при х→х0. Односторонние пределы. Свойства пределов.
- •Свойства пределов функции
- •22. Числовые последовательности и их пределы. Свойства пределов.
- •23. Бесконечно малые величины. Сравнение бесконечно малых. Бесконечно малые величины
- •Связь бесконечно малых величин с пределами функций
- •Свойства бесконечно малых величин
- •Сравнение бесконечно малых
- •24. Замечательные пределы: число е. Следствия из 2-го замечательного предела. Второй замечательный предел.
- •25. Непрерывность функции. Точки разрыва 1-го и 2-го рода.
- •26. Понятие производной. Геометрический и механический смысл. Определение производной
- •27. Дифференцируемость и непрерывность.
- •28. Правила дифференцирования. Производная сложной функции. Производная линейной функции. Производная суммы, произведения, частного. Производная логарифма.
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •29. Правила дифференцирования. Производная от обратной функции. Производная степенной и показательной функции. Логарифмическое дифференцирование.
- •30. Правила дифференцирования. Производные тригонометрических и обратных тригонометрических функций.
- •Производная сложной функции
- •31. Дифференциал функции. Геометрический смысл. Свойства. Инвариантность формы.
- •Инвариантность формы дифференциала
- •32. Производные высших порядков.
- •33. Дифференциалы высших порядков.
- •34. Правило Лопиталя.
Билет 1. Матрицы. Основные понятия
Определение.
Матрицей размера
![]() называется прямоугольная таблица,
содержащая m
строк и n
столбцов. Матрицы обозначают прописными
(заглавными) буквами A,
B,
C,
…, элементы матрицы – строчными буквами
с двойной индексацией aij,
где i
- номер строки, j
- номер столбца.
называется прямоугольная таблица,
содержащая m
строк и n
столбцов. Матрицы обозначают прописными
(заглавными) буквами A,
B,
C,
…, элементы матрицы – строчными буквами
с двойной индексацией aij,
где i
- номер строки, j
- номер столбца.
3)
Нулевая
матрица:
![]() ;
;
4)
Квадратная
матрица
– если
![]()
5)
Диагональная
матрица
(напр. 3-го порядка, где
![]() любые числа
любые числа
![]() ):
):
6) Единичная матрица, где все элементы, кроме главной диаг=0, а эл-ты глав диаг=1
7) Треугольная матрица – квадратн матр, у которой все элементы, расположенные по одну сторону от главной диагонали = 0. Бывают верхние и нижние 3угольные матрицы.
8) Матрицы произвольного размера называют квази3угольной, ступенчатой или трапециевидной.
9) Матрицы равны, если имеют одинаковые размер.
Билет 2. Действия над матрицами. Их св-ва.
1.Умножение матрицы на число.
Произведением матрицы A на число λ называется матрица B= λ *A ,элементы которой bij= λ*Aij для i=1,2..m, j=1,2..n. Если λ=0, то A*0=0 (нулевая матрица того же размера).
2.Сложение матриц.
Суммой матриц A и B одинакового размера m*n называется матрица C=A+B, элементы которой cij=aij+bij для i=1,2..m, j=1,2..n.
3.Вычитание матриц.
Разность матриц одинакового размера определяется как A-B=A+(-1)*B.
4.Умножение матриц.
Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц Am*k*Bk*n называется матрица C, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:
![]() ,
где
,
где
![]()
Свойства операций сложения и умножения матриц
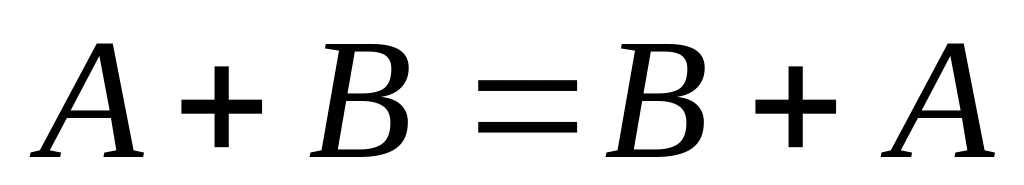 . 5)
. 5)
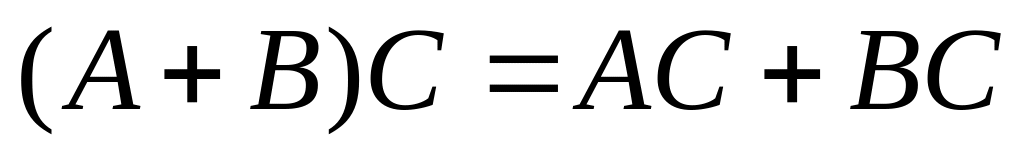 .
.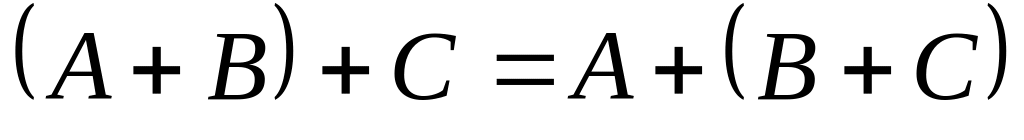 . 6)
. 6)
 .
.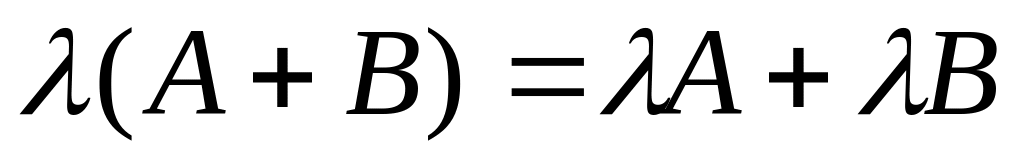 . 7)
. 7)
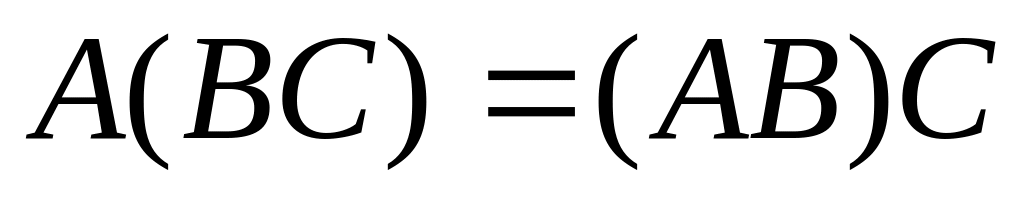 .
.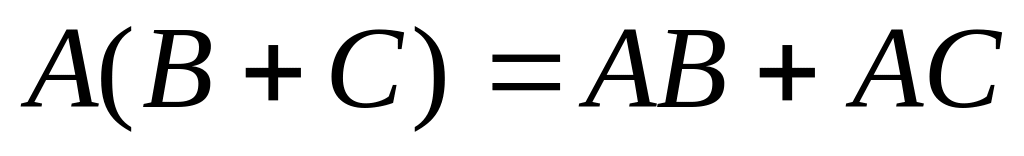 .
.
8)
![]() (в общем случае). Кроме того, если
(в общем случае). Кроме того, если
![]() существует, то
существует, то
![]() может вообще не существовать.
может вообще не существовать.
9)
![]()
![]() ,
где
,
где
![]() - единичная квадратная матрица.
- единичная квадратная матрица.
10)
Произведение двух ненулевых матриц
может равняться нулевой матрице, т.е.
если
![]() ,
то не следует, что
,
то не следует, что
![]() или
или
![]() .
.
5.Возведение в степень.
Целой
положительной степенью
![]() квадратной матрицы
квадратной матрицы
![]() называют
произведение
называют
произведение![]() матриц, равных
,
т.е.
матриц, равных
,
т.е.
![]() .
.
6.Транспонирование матриц.
Транспонирование
матрицы есть переход матрицы
к матрице
![]() ,
в которой строки и столбцы поменялись
местами с сохранением порядка. т.е. если
имеет размер
,
в которой строки и столбцы поменялись
местами с сохранением порядка. т.е. если
имеет размер
![]() ,
то
имеет размер
,
то
имеет размер
![]() .
.
Свойства операции транспонирования.
![]() .,
.,![]() ,
,![]() .,
.,![]()
Билет 3. Определители 2-го и 3-го порядков. Определения. Свойства.
Опред-ль 2-го порядка=минор, опред-ль 3-го пор-ка=алгебр дополн
Понятие определителя - число, характеризующее квадратную матрицу , необходимо для решения систем линейных алгебраических уравнений.
Определитель
матрицы
обозначают
![]() ,
дельта
(треугольник) ,det
A.
,
дельта
(треугольник) ,det
A.
1) Определителем матицы
1-го
порядка
![]() , называется элемент
, называется элемент
![]() :
:
![]() ;
;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
![]() .
Произведения
.
Произведения
![]() называются членами определителя 2-го
порядка.
называются членами определителя 2-го
порядка.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
Данная формула получила название правила треугольников или правило Сарруса.
При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:п
.
Свойства определителей
Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.
Если все элементы какой-либо строки (столбца) матрицы умножить на число ,то ее определитель умножится на это число .
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
При транспонировании матрицы ее определитель не изменяется:
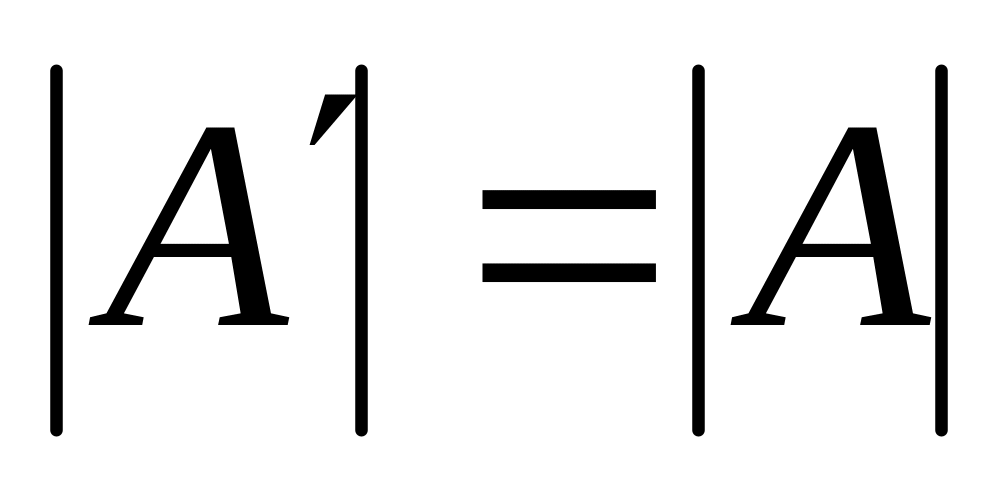 .
.При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
Если каждый элемент какого-либо столбца (строки) определителя – есть сумма двух слагаемых, то этот определитель – сумма двух определителей, причем в первом из них соответственно столбец (строка) состоит из первого слагаемого, а в другой – из второго.
Если элементы какого-либо столбца (строки) = 0, за исключением одного, то такой определитель равен этому, неравному 0, элементу, умноженному на его алгебраическое дополнение.
Сумма произведений произвольных чисел
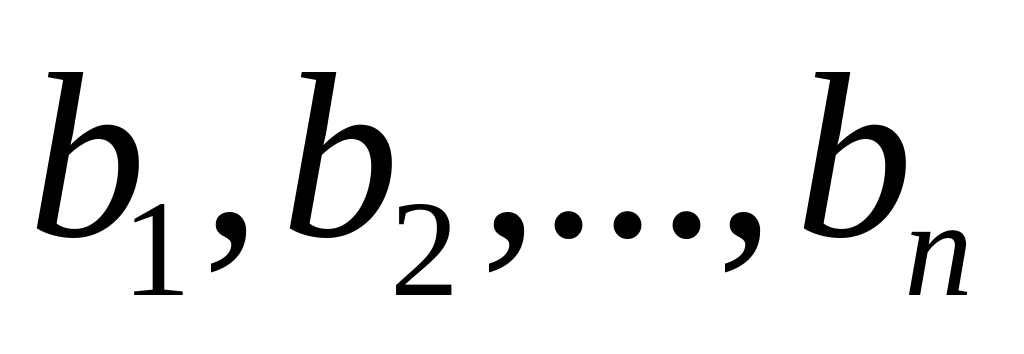 на алгебраические дополнения любой
строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на
числа
.
на алгебраические дополнения любой
строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на
числа
.
12.
Определитель произведения двух
квадратных матриц равен произведению
их определителей:
![]() ,
где
,
где
![]() ,
а
и
,
а
и
![]() - матрицы
- матрицы
![]() -го
порядка.
-го
порядка.
Перечисленные свойства определителей позволяют существенно упростить их вычисления для определителей высоких порядков. При этом с помощью свойств 1-9 желательно преобразовать исходную матрицу таким образом, чтобы она имела строку (столбец), содержащую как можно больше нулей, а потом вычислить определитель, разложенный по этой строке (столбцу).
Билет 4. Определители n-ного порядка. Вычисление. Свойства.
По той же формуле, что и определители 3-го определителя. 2 Метода: как и опред 3-го порядка, продолжая понижать///или приведение к треугольному виду: в этом случае опред-ль = произведению чисел на главн диагонали.
Билет 5. Обратная матрица. Определение. Вычисление.
Для
каждого числа
![]() существует обратное число
существует обратное число
![]() такое, что произведение
такое, что произведение
![]() .
Для квадратных матриц тоже вводится
аналогичное понятие.
.
Для квадратных матриц тоже вводится
аналогичное понятие.
Определение.
Матрица
![]() называется обратной по отношению к
квадратной матрице
,
если при умножении этой матрицы на
данную как справа, так и слева получается
единичная матрица: А-1*А=А*
А-1=Е.Только
квадратная матрица может иметь обратную,
однако не каждая квадратная матрица
имеет обратную.
называется обратной по отношению к
квадратной матрице
,
если при умножении этой матрицы на
данную как справа, так и слева получается
единичная матрица: А-1*А=А*
А-1=Е.Только
квадратная матрица может иметь обратную,
однако не каждая квадратная матрица
имеет обратную.
Определение.
Матрица
является
невырожденной
(неособенной),
если |A|≠0, в противном случае при
![]() матрица
называется вырожденной
(особенной).
матрица
называется вырожденной
(особенной).
Теорема
(необходимое
и достаточное условие существования
обратной матрицы).
Обратная матрица
существует (и единственна) тогда и
только тогда, когда исходная матрица
является невырожденной (неособенной)
и вычисляется по формуле: А-1=1/|A|
*A^,
где A^
- присоединенная матрица, состоящая из
алгебраических дополнений элементов
транспонированной матрицы, т.е.
![]() .
.
