
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 8
- •Вопрос 9
- •Формальные свойства алгоритмов
- •Вопрос 10
- •Виды алгоритмов
- •Вопрос 12
- •Вопрос 13
- •3.2 Графический способ записи алгоритмов
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Вопрос 20
- •Вопрос 21
- •Вопрос 62
- •Вопрос 22
- •Вопрос 23
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 37
- •Вопрос 39
- •Вопрос 40
- •Visual Basic. Типы данных в языке.
- •Вопрос 41
- •Вопрос 42
- •Вопрос 43
- •Вопрос 44
- •Вопрос 45 Математические функции
- •Функции преобразования данных
- •Функции даты и времени
- •Вопрос 46
- •Вопрос 47 Строковые функции
- •Вопрос 48
- •Visual Basic. Основные операторы.
- •Вопрос 49
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Вопрос 53
- •Вопрос 54
- •Вопрос 55
- •Вопрос 57
- •Вопрос 59
- •Вопрос 60
- •Вопрос 61
- •Вопрос 62
- •Вопрос 63
- •1) Функция uBound служит для определения верхней границы (индекса самого последнего элемента) массива по заданному измерению.
- •2) Функция lBound (Lower Bound) служит для определения нижней границы (индекса самого первого элемента) массива по заданному измерению.
- •3) IsArray Служит для проверки, является ли переменная массивом. Применение функции IsArray особенно полезно для переменных типа Variant, содержащих массивы.
- •4) Функция Array служит для обработки массивов.
- •Вопрос 64
- •Характерные ошибки программирования
Вопрос 26
Числа Фибоначчи — элементы числовой последовательности
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного какФибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более
формально, последовательность чисел
Фибоначчи ![]() задается линейным
рекуррентным соотношением:
задается линейным
рекуррентным соотношением:
![]()
Иногда
числа Фибоначчи рассматривают и для
отрицательных номеров n как
двусторонне бесконечную последовательность,
удовлетворяющую тому же рекуррентному
соотношению. При этом члены с отрицательными
индексами легко получить с помощью
эквивалентной формулы «назад»: ![]() :
:
-
n
−10
−9
−8
−7
−6
−5
−4
−3
−2
−1
0
1
2
3
4
5
6
7
8
9
10
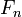
−55
34
−21
13
−8
5
−3
2
−1
1
0
1
1
2
3
5
8
13
21
34
55
Легко
заметить, что ![]() .
.
Свойства:
Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е.
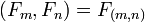 .
Следствия:
.
Следствия: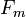 делится
на
тогда
и только тогда, когда
делится
на
тогда
и только тогда, когда 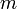 делится
на
делится
на 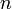 (за
исключением
(за
исключением 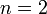 ).
В частности,
делится
на
).
В частности,
делится
на 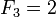 (то
есть является чётным) только
для
(то
есть является чётным) только
для 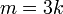 ;
делится
на
;
делится
на 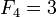 только
для
только
для 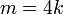 ;
делится
на
;
делится
на 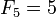 только
для
только
для 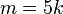 и т. д.
и т. д.может быть простым только для простых (с единственным исключением
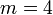 ).
Например, число
).
Например, число 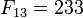 простое,
и его индекс 13 также прост. Обратное
не верно, наименьший контрпример —
простое,
и его индекс 13 также прост. Обратное
не верно, наименьший контрпример — 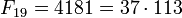 .
Неизвестно, бесконечно ли множество
чисел Фибоначчи, являющихся простыми.
.
Неизвестно, бесконечно ли множество
чисел Фибоначчи, являющихся простыми.
Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен
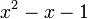 имеет
корни
имеет
корни  и
и 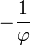 .
.Отношения
 являются подходящими
дробями золотого
сечения
являются подходящими
дробями золотого
сечения  и,
в частности,
и,
в частности, 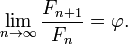
Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
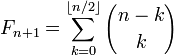 .
.
В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Производящей функцией последовательности чисел Фибоначчи является:
![]()
Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена
![]()
на множестве неотрицательных целых чисел x и y.[4]
Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:
1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
Натуральное число N является числом Фибоначчи тогда и только тогда, когда
 или
или 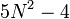 является квадратом.[5]
является квадратом.[5]Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[6]
Число Фибоначчи
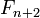 равно
количеству кортежей длины n из
нулей и единиц, в которых нет двух
соседних нулей. При этом
равно
количеству таких кортежей, начинающихся
с нуля, а
равно
количеству кортежей длины n из
нулей и единиц, в которых нет двух
соседних нулей. При этом
равно
количеству таких кортежей, начинающихся
с нуля, а 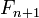 —
начинающихся с единицы.
—
начинающихся с единицы.
Задача о кроликах
Пусть имеется пара кроликов. Известно, что от каждой пары кроликов каждый месяц рождается новая пара кроликов, которая в свою очередь становится способной производить потомство в возрасте одного месяца. Требуется определить, сколько пар кроликов будет через n месяцев.
Вначале изложим историю этой задачи, затем её решение и другие задачи связанные с ней.
Говоря об античной математике, каждый назовет таких математиков, как Евклид, Пифагор, Герон и др. Одним из самых знаменитых математиков средних веков, наравне с Виетом был Леонардо из Пизы, известный под именем Фибоначчи (сокращенное filius Bonacci, т.е. сын Боначчи).
Фибоначчи родился в Италии в 1175г., был воспитан на Севере Африки, где его отец занимал пост дипломата. Вернувшись в Италию, в 1202г. публикует математический трактат под названием "Liber abacci". Этот трактат, содержавший почти все арифметические и алгебраические сведения того времени, сыграл главную роль в течении последующих столетий в развитии математики в Европе. В частности, на основе этого трактата, европейцы познакомились с арабскими цифрами, т.е. с позиционной системой исчисления. Также Фибоначчи публикует: в 1220г. "Practica geometrica", в 1225, "Liber quadratorum". Трактат "Liber abacci" был переиздан в 1228г. Одна из задач упоминаемая в "Liber abacci" называется "задача о кроликах" (с.123-124 издания 1228г.), представленная в начале этого материала.
Перейдем к решению этой задачи.
Пусть fn число пар кроликов после n месяцев. Число пар кроликов после n + 1 месяцев fn+1, будет равно числу пар на n-ом месяце, т.е. fn, плюс число пар новорожденных кроликов. Поскольку кролики рождаются от пары кроликов возраста больше одного месяца, новорожденных кроликов будет fn-1 пар. Следовательно, справедливо соотношение
fn+1 = fn + fn-1, |
(1) |
причем
f0 = 0 f1 = 1. |
(2) |
Таким образом получим рекуррентную числовую последовательность
0, 1, 1, 2, 3, 5, 8, ... |
(3) |
которая была названа рядом Фибоначчи. Каждый член этой последовательности, начиная с третьего, равен сумме двух предыдущих. Первые два члена считаются заданными f0 = 0, f1 = 1.
Таким образом, "задача о кроликах" свелась к решению функционального уравнения (1), т.е. к нахождению общего члена последовательности fn удовлетворяющего соотношению (1) при условиях (2).
Предположим, что последовательность fn имеет вид
fn = ln, |
(4) |
где l - вещественный параметр.
Подставив fn в (1) получим
ln+1 = ln + ln-1,
или, эквивалентно,
ln-1(l2 - l - 1) = 0.
Так как fn № 0 ("n О N*), последнее равенство принимает вид
l2 - l - 1 = 0, |
(5) |
которое представляет собой квадратное уравнение по отношению к действительному параметру l. Из (5) получим
![]()
![]()
Таким образом, последовательности
![]()
удовлетворяют равенству (1). Отсюда заключаем, что уравнение (1) имеет много решений. В общем, существует бесконечное число последовательностей, удовлетворяющих (1). Легко заметить, что последовательность вида
|
(6) |
где c1, c2 - фиксированные действительные константы, также удовлетворяет (1). Более того, можно показать, что любая последовательность, удовлетворяющая равенству (1) имеет вид (6). Имея другие цели, не будем доказывать этот факт в рамках этой работы. Для интересующихся общей теорией решения уравнений вида (1), называемых уравнениями в конечных разностях, рекомендуем обратиться к литературе [1]-[4].
Возвращаясь к последовательности Фибоначчи, отметим, что эта последовательность однозначно определена, и однозначность обеспечивается первыми двумя членами, т.е. начальными условиями (2). Подставляя n = 0 и n = 1 в (6), получим линейную систему
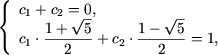
с
решением ![]()
В результате получим, что n-ый член последовательности Фибоначчи имеет вид
|
