2.2. Уравнения Колмогорова для вероятностей состояний

Введем обозначения:

P_k(t) – вероятность того, что система в момент времени t находится в состоянии S_k(k=0, 1, 2, …, N);

P_ik(t) – условная вероятность того, что система, будучи в момент t в состоянии S_i, за время перейдет в состояние S_k(ki).

Так как P_ik(t) – вероятность появления хотя бы одного события за время t, то

,

где _ik – интенсивность потока событий, под воздействием которого система переходит из состояния S_i в состояние S_k .

Разлагая показательную функцию в ряд Тейлора, имеем:

. (2.5)

Пусть в момент времени t система находится в одном из возможных состояний. Определим вероятность P_k(t+) того, что в момент t+t она будет находиться в состоянии S_k (k=0,1,…,N).

Предположим, что за время t система может только один раз изменить свое состояние. Это означает, что система может попасть в состояние S_k двумя способами.

1. В момент t система находилась в одном из состояний S_i(ik), которое соединено дугой (i, k) с состоянием S_k , а за время t перешла в состояние S_k . Вероятность этого события , где – множество дуг, заходящих в вершину S_k . Например, для состояния S₁ (рис. 2.1) , P₁=P₀(t)P₀₁(t)+P₂(t)P₂₁(t) .

2. В момент t система находилась в состоянии S_k и за время t не вышла из него ни по одной из дуг, исходящих из вершины S_k.. Вероятность этого события , где – множество дуг, исходящих из вершины S_k . Для состояния S₁ (рис. 2.1) , P₂=P₁(t)[1–P₁₀(t)–P₁₂(t)] , где [P₁₀(t)+P₁₂(t)] – вероятность того, что система, будучи в момент t в состоянии S₁, за время t перейдет из него в состояние S₀ или S₂.

Так как оба способа несовместны, то

(2.6)

Перенесем P_k(t) в левую часть и разделим все члены уравнения (2.6) на t, получим

.

В результате предельного перехода при t0 с учетом выражения (2.5) получим систему дифференциальных уравнений Колмогорова

(2.7)

Уравнение (2.7) в отличие от уравнения (2.6) является точным, так как члены, соответствующие двум и более переходам системы за время t и опущенные в выражении (2.6), в результате предельного перехода обращаются в нуль. Действительно, пусть за время t система может перейти из состояния S_i в состояние S_k через состояние S_j. Условная вероятность этого события с учетом формулы (2.5)

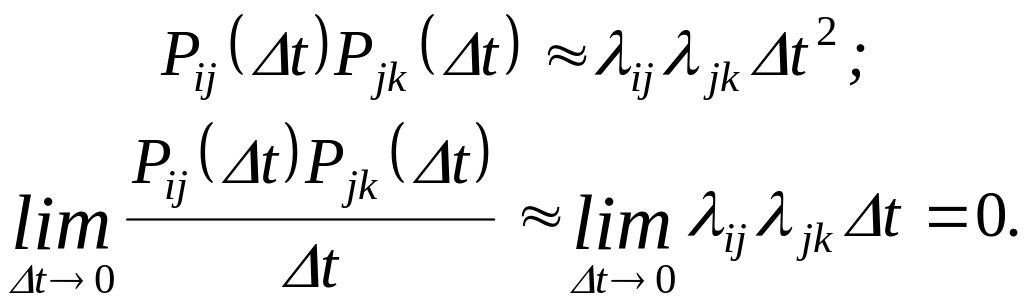
При записи правой части уравнения (2.7) целесообразно руководствоваться мнемоническим правилом : «то, что втекает, прибавляется, а что вытекает – вычитается».

Для рассматриваемого примера (рис 2.1) уравнения Колмогорова имеют вид (читателю рекомендуется записать их самостоятельно)

Интегрируя систему линейных дифференциальных уравнений (2.7) с учетом условия нормировки (2.1) при заданных начальных условиях (например, P_k(0)=1, а для всех i  k P_i(0)=0 – в начальный момент система находится в состоянии S_k), можно определить распределение для вероятностей состояний системы в любой момент времени.

На практике часто наибольший интерес представляет поведение системы в установившемся режиме при t. Здесь сразу же возникает вопрос, как поведут себя вероятности P_k(t) при t, стремятся ли они к каким либо пределам, существует ли в системе некоторый установившийся (стационарный) режим.

Предельные вероятности существуют и не зависят от начального состояния системы, если граф ее состояний конечен и существует маршрут между любой парой его вершин, то есть система может перейти из каждого состояния в любое другое за конечное число шагов. Такие системы называют эргодическими.

Предельная вероятность P_k – это средняя доля времени, в течение которого система находится в состоянии S_k . Если, например, P_k=0,3, то это означает, что в состоянии S_k система времени ее функционирования.

Для вычисления предельных вероятностей в уравнениях (2.7) производные приравнивают нулю и получают систему линейных алгебраических уравнений

(2.8)

Так как система (2.8) однородна, то при вычислении вероятностей P_k одно из уравнений (2.8) заменяют нормировочным условием

.

При аналитическом исследовании удобно использовать следующий способ решения системы (2.8): сначала все предельные вероятности выражают через какую-либо одну, а затем их подставляют в условие нормировки.