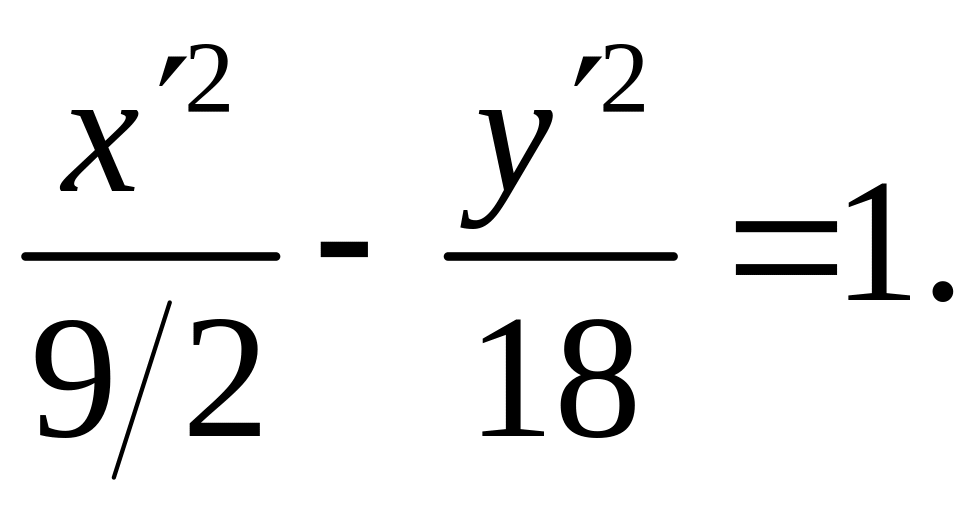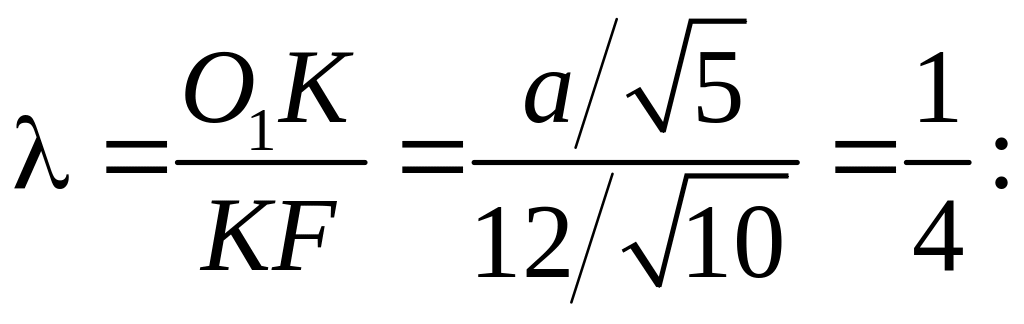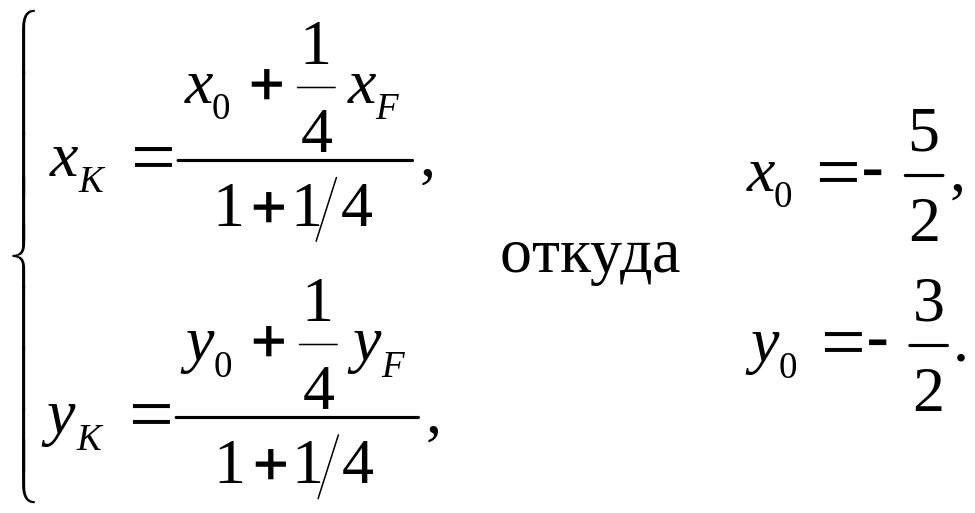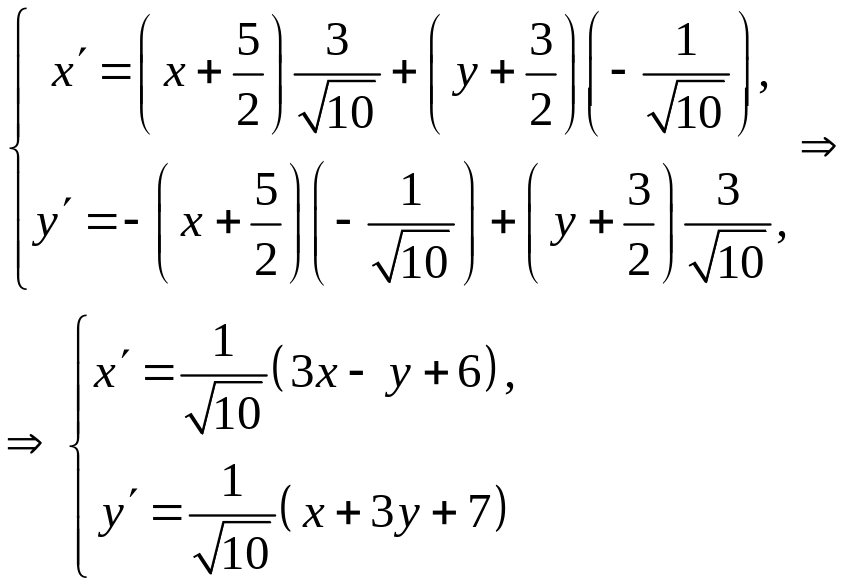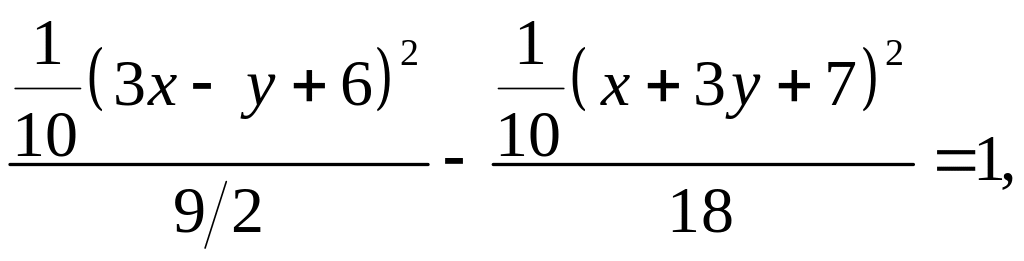Пп 7.3. Преобразования координат основные определения и формулы
Преобразования координат
1. Параллельный перенос
П еренесём
начало координат из точки О
в точку О1
параллельным переносом осей. Пусть в
системе координат xoy
точка М
имеет координаты x
и y.
Система координат xO1y
получена из системы координат xOy
параллельным переносом осей, при котором
начало координат О1
имеет координаты x0
и y0
в системе координат xOy.
Точка М
в системе координат xO1y
имеет координаты x
и y.
Связь между координатами точки M(x,y)
и точки M(x,y)
в старой и новой системах координат
задается формулами:
еренесём
начало координат из точки О
в точку О1
параллельным переносом осей. Пусть в
системе координат xoy
точка М
имеет координаты x
и y.
Система координат xO1y
получена из системы координат xOy
параллельным переносом осей, при котором
начало координат О1
имеет координаты x0
и y0
в системе координат xOy.
Точка М
в системе координат xO1y
имеет координаты x
и y.
Связь между координатами точки M(x,y)
и точки M(x,y)
в старой и новой системах координат
задается формулами:
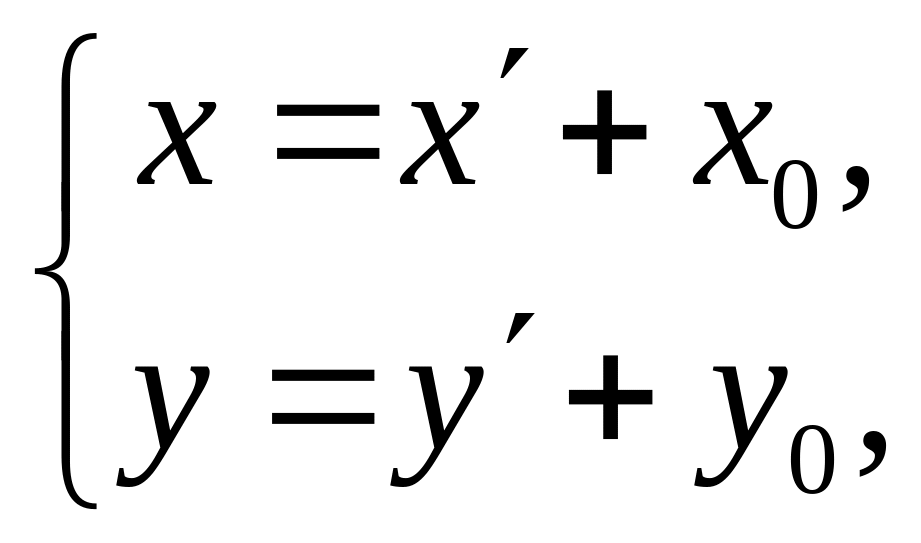 (1)
(1)
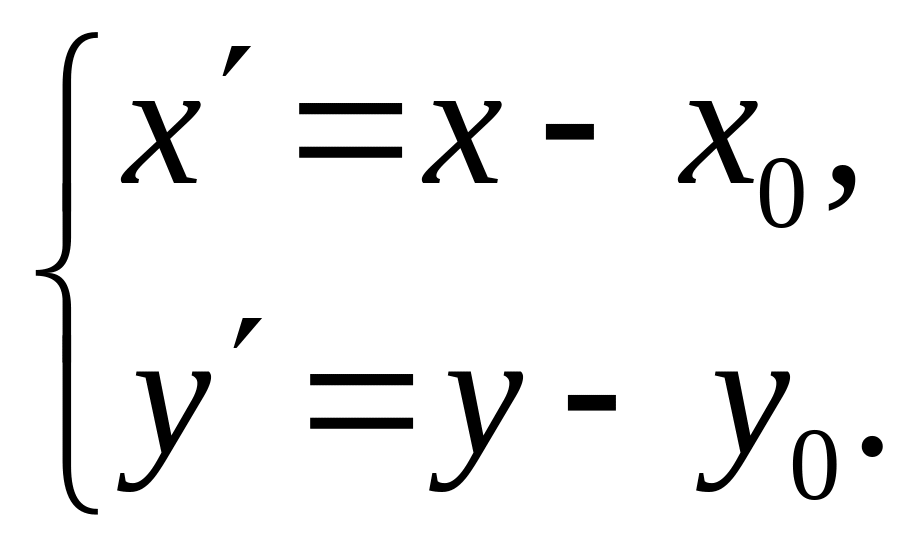 (2)
(2)
У равнения
кривых второго порядка, когда их центры
симметрии находятся в точке с координатами
O1(x0,y0),
получаются с помощью преобразования
координат при параллельном переносе
осей (2).
равнения
кривых второго порядка, когда их центры
симметрии находятся в точке с координатами
O1(x0,y0),
получаются с помощью преобразования
координат при параллельном переносе
осей (2).
![]() -
уравнение окружности с центром в точке
O1(x0,y0)
и радиусом R.
-
уравнение окружности с центром в точке
O1(x0,y0)
и радиусом R.
Аналогично получаются уравнения других кривых второго порядка:
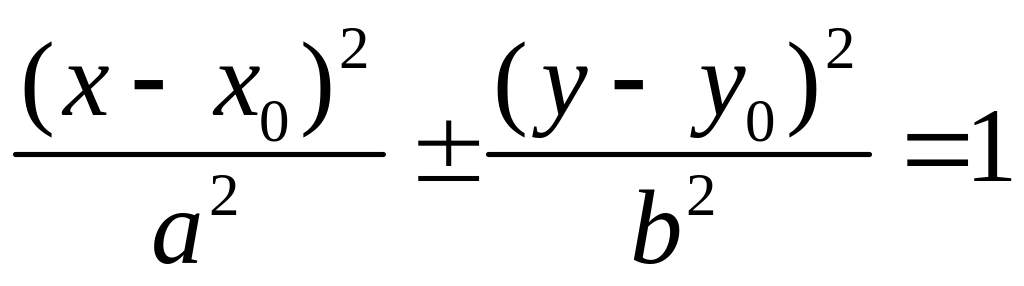 -
уравнения эллипса и гиперболы с центром
симметрии в точке O1(x0,y0);
-
уравнения эллипса и гиперболы с центром
симметрии в точке O1(x0,y0);
![]() -
уравнение параболы с вершиной в точке
O1(x0,y0).
-
уравнение параболы с вершиной в точке
O1(x0,y0).
При
этом, например, уравнения директрис
эллипса и гиперболы:
![]() ,
а параболы:
,
а параболы:
![]() .
Аналогично преобразуются и уравнения
асимптот гиперболы:
.
Аналогично преобразуются и уравнения
асимптот гиперболы:
![]() .
.
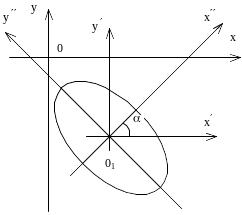
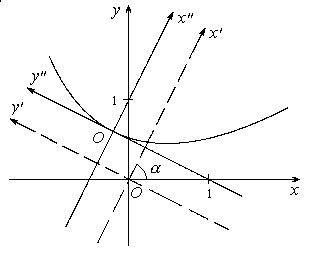
2 . Поворот координатных осей
Выведем формулу преобразования координат при повороте координатных осей.
Повернём
оси координат на угол
относительно исходной системы координат.
Координаты точки М
в системе
координат xOy
равны x
и y.
Найдём её координаты в системе координат
xOy.
В треугольнике CMD
![]() ,
OD =
x,
MD =
y.
,
OD =
x,
MD =
y.
Следовательно,
x = OA = OB – AB = OB - CD, y = MA = AC + CM = DB + CM.
Поскольку

то
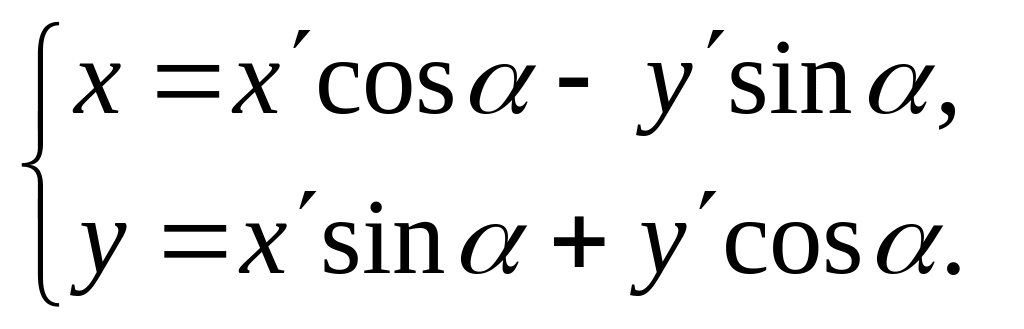 (3)
(3)
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x,y) этой же точки при повороте осей на угол .
Формулы, выражающие новые координаты (x,y) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол , то старая система получается поворотом новой на угол (-), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно на (-).
Выполнив это преобразование, получим
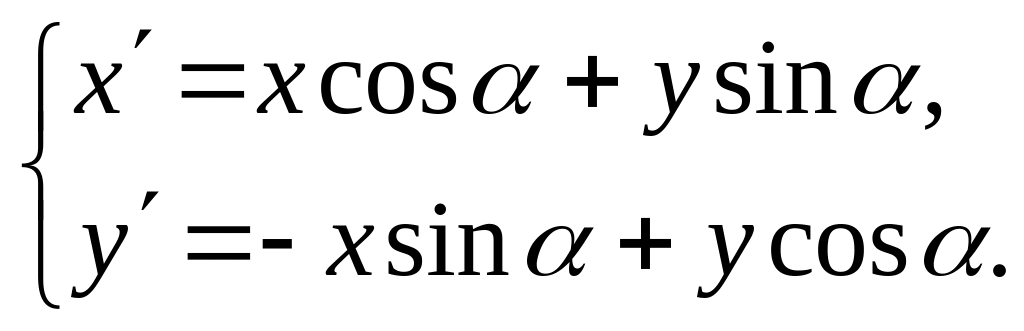
При этом, например, уравнения директрис эллипса (гиперболы) и параболы принимают вид:
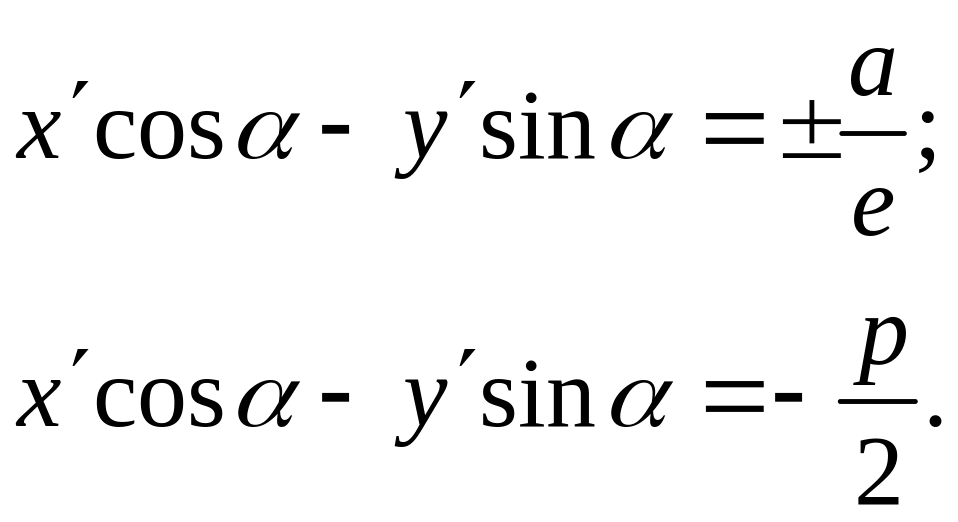
3. Изменение начала координат и поворот осей
Если оси декартовой прямоугольной системы переносятся параллельно на величины x0 по оси ox и на y0 по оси oy и, кроме того, поворачиваются на угол , то этому изменению системы соответствуют формулы преобразования координат, выражающие старые координаты через новые:
 (4)
(4)
и новые координаты через старые:
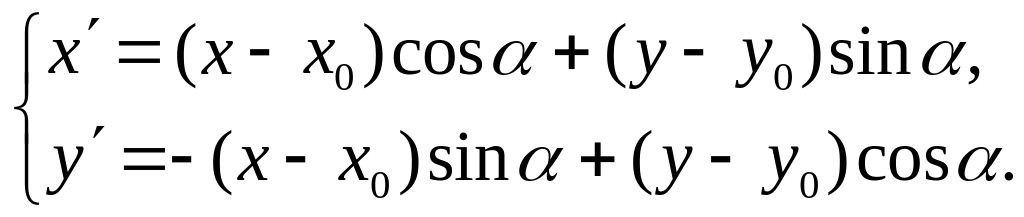 (5)
(5)
4. Приведение общего уравнения кривой второго порядка к каноническому виду
Пусть кривая второго порядка задана в общем виде:
![]() .
.
Приведение этого уравнения к каноническому виду заключается в нахождении системы координат, в которой кривая имеет канонический вид, геометрически это может быть достигнуто переносом начала координат в центр кривой (x0,y0) и поворотом координатных осей на угол, совмещающий оси симметрии кривой с координатными осями. Алгебраически это приводит к исчезновению членов с произведением текущих координат и членов, содержащих их в первой степени, после применения формул (1) и (3).
Уравнения, определяющие центр кривой, если он существует, записываются как
![]() (6)
(6)
Кривые второго порядка, имеющие единственный центр, называются центральными. После переноса начала координат в центр (x0,y0) уравнение кривой примет вид
![]() , (7)
, (7)
где
![]() .
.
Чтобы получить каноническое уравнение кривой
![]() ,
,
подвергнем уравнение
(7) преобразованию поворота осей координат
на угол
![]() .
.
После преобразования получим:
![]()
где
![]() -
новые координаты.
-
новые координаты.
Выпишем из преобразованного уравнения слагаемые второго порядка:
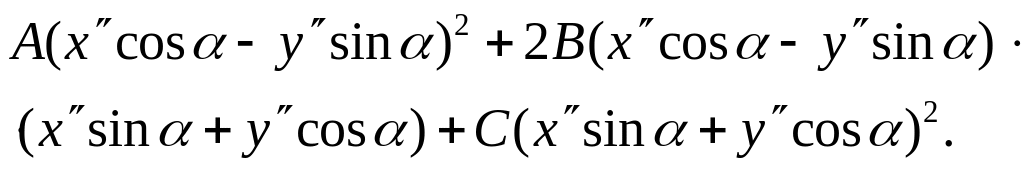
Из
этих слагаемых нас интересует слагаемое,
содержащее произведение
![]() ,
коэффициент перед которым равен
,
коэффициент перед которым равен

Найдём
угол поворота из условия В1=0:
![]() .
.
Если
А = С,
то
![]() и в качестве угла поворота можно выбрать
и в качестве угла поворота можно выбрать
![]() ;
если
;
если
![]() ,
то выбираем
,
то выбираем
![]() .
.
ПП 7.3. Преобразования координат
|
|
ПП 7.3. № 1 |
Преобразовать уравнение x2 – y2 = a2 поворотом осей на 45 против часовой стрелки. Решение
Так как
= -45,
то
Отсюда преобразование поворота принимает вид:
Подстановка в исходное уравнение дает ху = а2/2. |
ПП 7.3. № 2 |
Привести уравнение 5x2 + 9y2 – 30x + 18y + 9 = 0 к каноническому виду и построить кривую. Решение Сгруппируем члены этого уравнения, содержащие одноименные координаты: (5x2 – 30x) + (9y2 + 18y) +9 = 0, или 5(x2 – 6x) + 9(y2 + 2y) +9 = 0. Дополняем члены в скобках до полных квадратов: 5(x2 – 6x + 9 – 9) + 9(y2 + 2y + 1 – 1) +9 = 0, или 5(x – 3)2 + 9(y + 1)2 = 45. Обозначаем x = x – 3, y = y + 1, x0 = 3, y0 = -1, то есть точка О1(3, -1) – центр кривой. Уравнение в новой системе координат принимает вид:
|
ПП 7.3. № 3 |
Определить вид
кривой
Решение Определим угол поворота осей по формуле (7) п.4.4:
Подвергнем уравнение кривой преобразованию:
и получим уравнение эллипса
x 2 + 2y 2 = 2. |
ПП 7.3. № 4 |
Установить, какую линию определяет уравнение x2 + y2 + xy – 2x + 3y = 0. Решение Перенесем начало координат в такую точку О1(х0, у0), чтобы уравнение не содержало х и у в первой степени. Это соответствует преобразованию координат:
Подстановка в исходное уравнение дает (x + x0)2 + (x + x0)(y + y0) + (y + y0)2 – 2(x + x0) + 3(y + y0) = 0 или x2 + xy + y2 + (2x0 + y0 - 2)x + (x0 + 2y0 + 3)y + x02 + x0y0 + y02 - 2x0 + 3y0 =0. Положим 2x0 + y0 – 2 = 0, x0 + 2y0 + 3 = 0. Решение полученной системы уравнений: x0 = 7/3 и y0 = -8/3. Таким образом, координаты нового начала координат O1(7/3, -8/3), а уравнение принимает вид x2 + xy + y 2 = 93/25. Повернем оси координат на такой угол , чтобы исчез член ху. Подвергнем последнее уравнение преобразованию:
и получим (cos2 + sincos + sin2)x2 + (cos2 - sin2)xy + + (sin2 - sincos + cos2)y 2 = 93/25. Полагая cos2 - sin2 = 0, имеем tg2 = 1. Следовательно, 1,2 = 45.
Возьмем
= 45,
cos45
= sin45
=
После
соответствующих вычислений получаем
Итак,
в дважды штрихованной системе координат, получаемой из исходной параллельным переносом осей координат в точку О1(7/3, -8/3) и последующим поворотом на угол 45 против часовой стрелки. Уравнение
x2
+ y2
+ xy – 2x
+ 3y
= 0 приведено
к каноническому виду
|
ПП 7.3. № 5 |
Привести к каноническому виду уравнение 4x2 – 4xy + y2 – 2x – 14y + 7 = 0. Решение Система уравнений для нахождения центра кривой:
значит, данная
кривая центра не имеет. Не меняя начала
координат, повернем оси на некоторый
угол ,
соответствующие преобразования
координат имеют вид:
Перейдем в уравнении к новым координатам: 4x2 – 4xy + y2 – 2x – 14y + 7 = (4cos2 - 4cossin + sin2)x2 + + 2(-4sincos - 2cos2 + 2sin2 + sincos)xy + + (4sin2 + 4sincos + cos2)y2 + + 2(-cos - 7sin)x + 2(sin - 7cos)y + 7 = 0. (*) Постараемся теперь подобрать угол так, чтобы коэффициент при ху обратился в нуль. Для этого нам придется решить тригонометрическое уравнение -4sincos - 2cos2 + 2sin2 + sincos = 0. Имеем 2sin2 - 3sincos - 2cos2 = 0, или 2tg2 - 3tg - 2 = 0. Отсюда tg = 2, или tg = -1/2. Возьмем первое решение, что соответствует повороту осей на острый угол. Зная tg, вычислим cos и sin:
Отсюда, и учитывая (*), находим уравнение данной кривой в системе х,у:
Дальнейшее упрощение уравнения (**) производится при помощи параллельного перенесения осей Ох, Оу. Перепишем уравнение (**) следующим образом:
Дополнив выражение в первой скобке до полного квадрата разности и компенсируя это дополнение надлежащим слагаемым, получим:
Введем теперь еще новые координаты х,у, полагая
x
= x
+
что
соответствует параллельному перемещению
осей на величину
Это
есть каноническое уравнение параболы
с параметром
|
ПП 7.3. № 6 |
Какую линию определяет уравнение 4x2 - 4xy + y2 + 4x - 2y - 3 =0? Решение Система для нахождения центра кривой в данном случае имеет вид:
Эта система равносильна одному уравнению 2х0 – у0 + 1 = 0, следовательно, линия имеет бесконечно много центров, составляющих прямую 2х – у + 1= 0. Заметим, что левая часть данного уравнения разлагается на множители первой степени:
4х2 – 4ху + у2 + 4х –2у –3 = (2х – у +3)(2х – у – 1). Значит, рассматриваемая линия представляет собой пару параллельных прямых: 2х – у +3 = 0 и 2х – у – 1 = 0.
|
ПП 7.3. № 7 |
1. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 12 = 0 приводится
к каноническому виду х
2
+ 4у
2
+ 4 = 0, или
Это уравнение похоже на каноническое уравнение эллипса. Однако оно не определяет на плоскости никакого действительного образа, так как для любых действительных чисел х,у левая часть его не отрицательна, а cправа стоит –1. Такое уравнение и аналогичные ему называются уравнениями мнимого эллипса. 2. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 4 = 0 приводится
к каноническому виду х
2
+ 4у
2
= 0, или
Уравнение также похоже на каноническое уравнение эллипса, но определяет не эллипс, а единственную точку: х = 0, у = 0. Такое уравнение и аналогичные ему называются уравнениями вырожденного эллипса.
|
ПП 7.3. № 8 |
Составить уравнение параболы, если ее фокус находится в точке F(2, -1) и уравнение директрисы D: x – y – 1 = 0. Решение Пусть в некоторой системе координат хО1у парабола имеет канонический вид у2 = 2рх. Если прямая у = х – 1 является ее директрисой, то оси системы координат хО1у параллельны директрисе. Координаты вершины параболы, совпадающей с новым началом координат О1, найдем как середину отрезка нормали к директрисе D, проходящей через фокус.
И Откуда b = 1 и О1х: у = -х + 1. Координаты точки K пересечения директрисы и оси О1х находим из условия:
Координаты нового начала координат О1(х0, у0):
Итак,
уравнение параболы в старой системе
координат получим, если подвергнем
уравнение параболы y
2
=
|
ПП 7.3. № 9 |
Написать уравнение
гиперболы, если известны ее эксцентриситет
е = Решение Уравнение
директрисы D1:
у = 3х
+ 3 позволяет
заключить, что новая ось координат
Ох
имеет вид y
= (-1/3)x
+ b, проходит
через точку F(2,
-3), значит,
Пусть начало
новой системы координат находится в
точке О1(х0,
у0).
Найдем координаты точки К
как координаты точки пересечения
директрисы D1
и
оси Ох
из системы
Геометрические
свойства гиперболы, которая в новых
осях координат Оху
имеет вид
F(2, -3) до директрисы D1: 3х – у + 3 = 0.
Уравнение
гиперболы в новых координатах имеет
вид
Координаты
нового центра найдем, зная что точка
К делит
отрезок О1F
в отношении
Из
АВО:
sin
=
и
уравнение гиперболы принимает вид
4(3х – у +6)2 – (х + 3у + 7)2 = 180 или 7х2 – у2 – 6ху – 18у + 26х + 17 = 0.
|

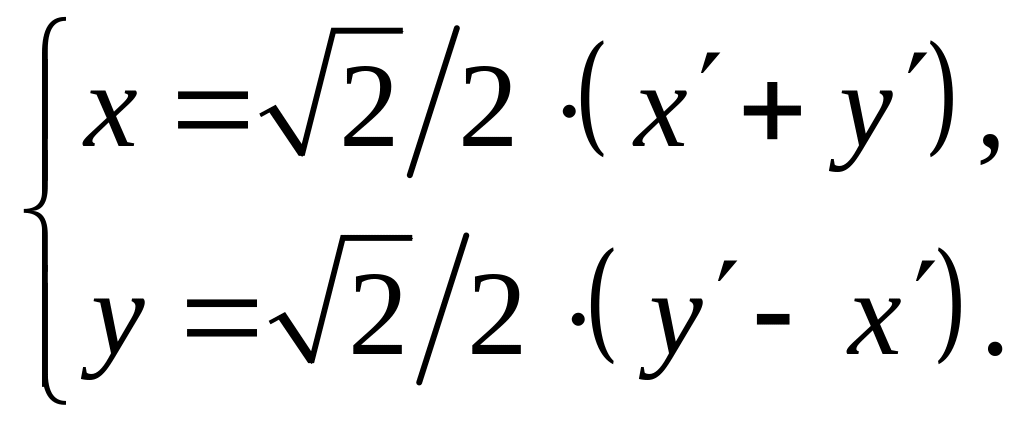
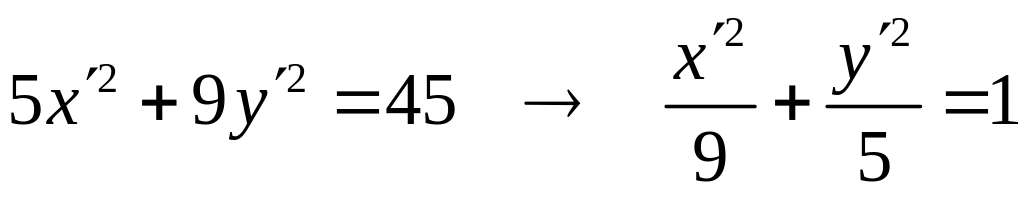 и определяет
эллипс с полуосями а
= 3, b =
и определяет
эллипс с полуосями а
= 3, b =

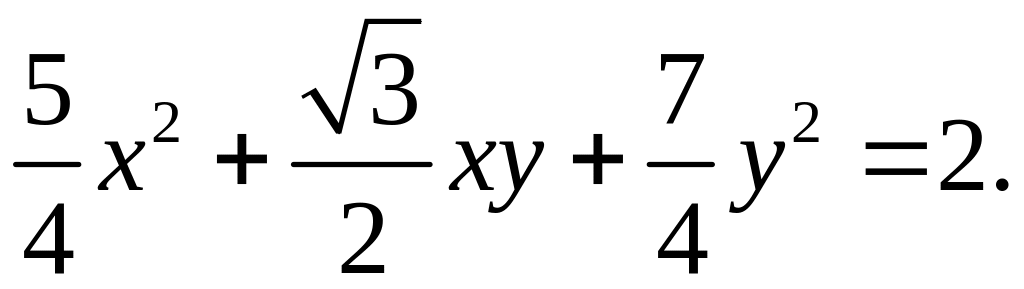
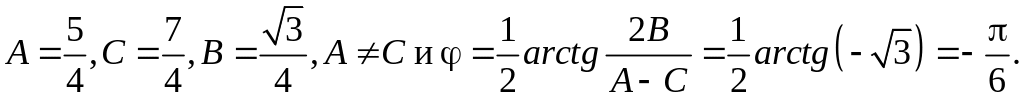
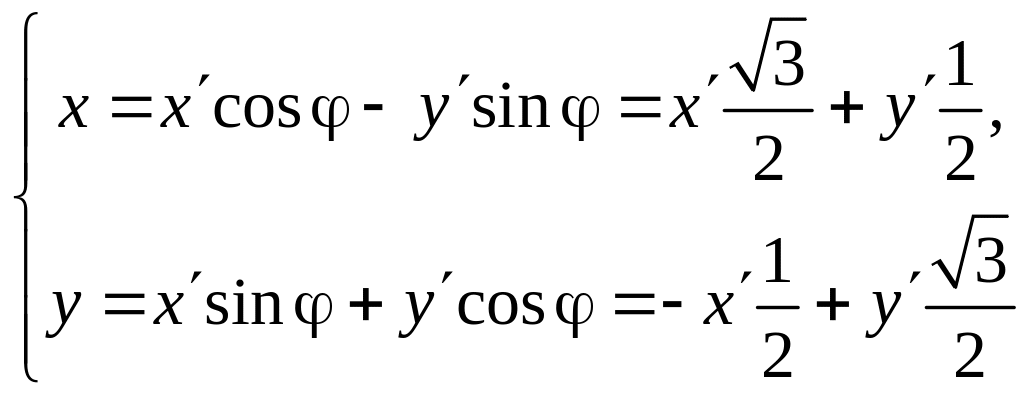
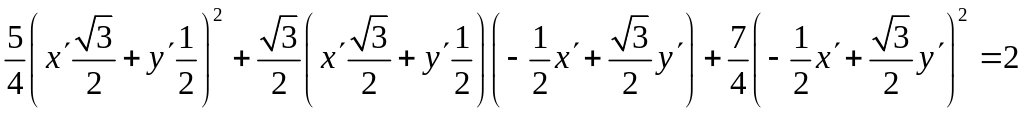 .
.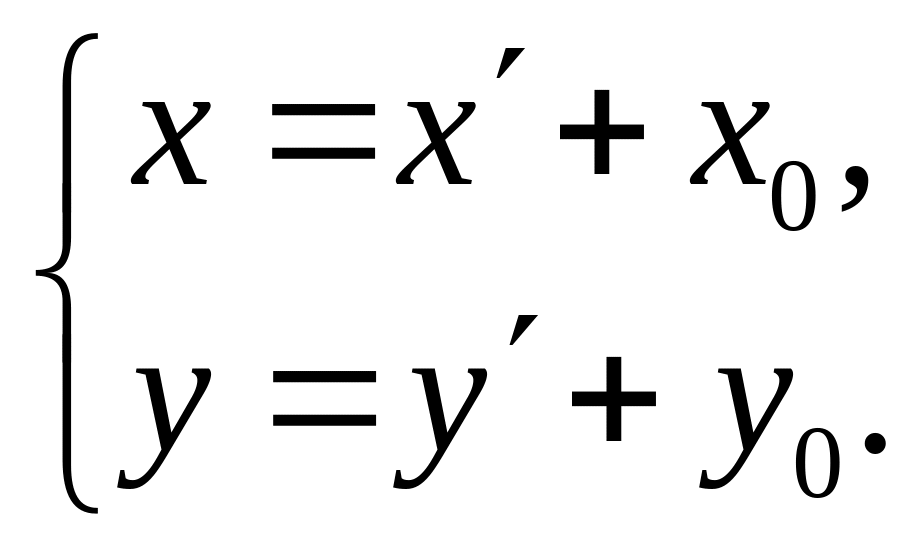
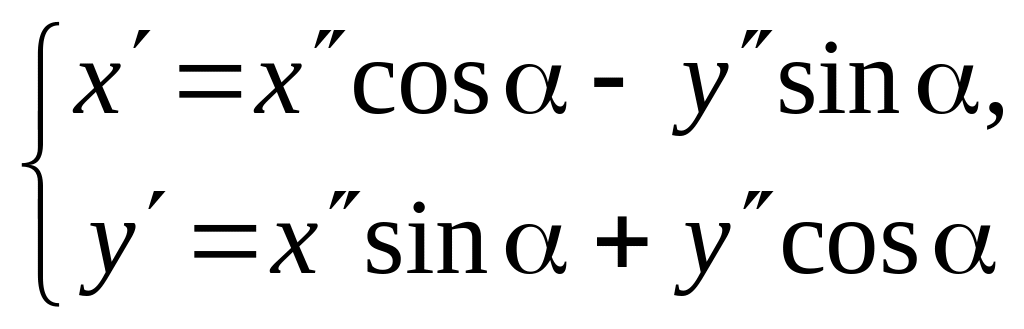
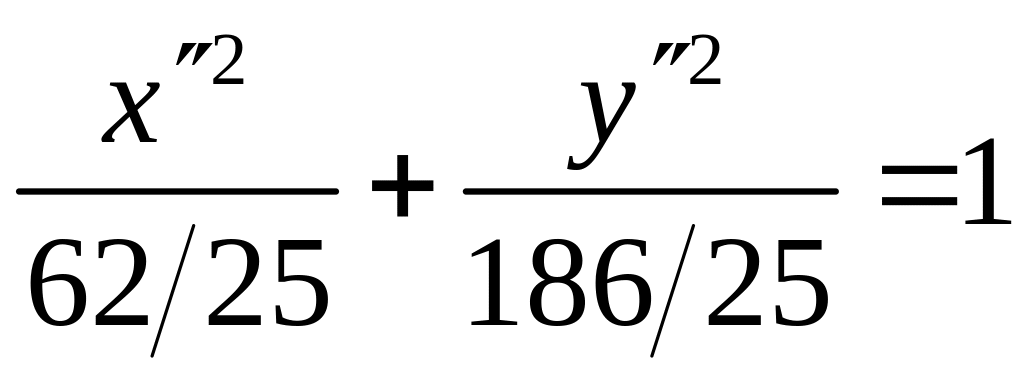

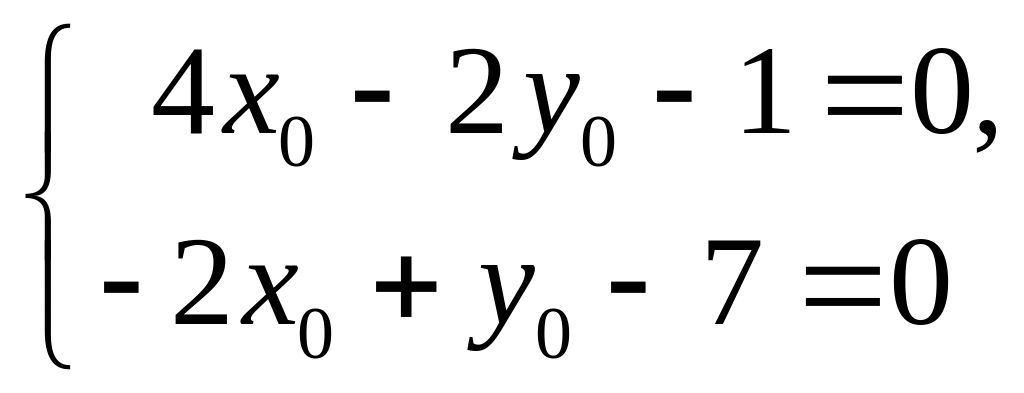 несовместна,
несовместна,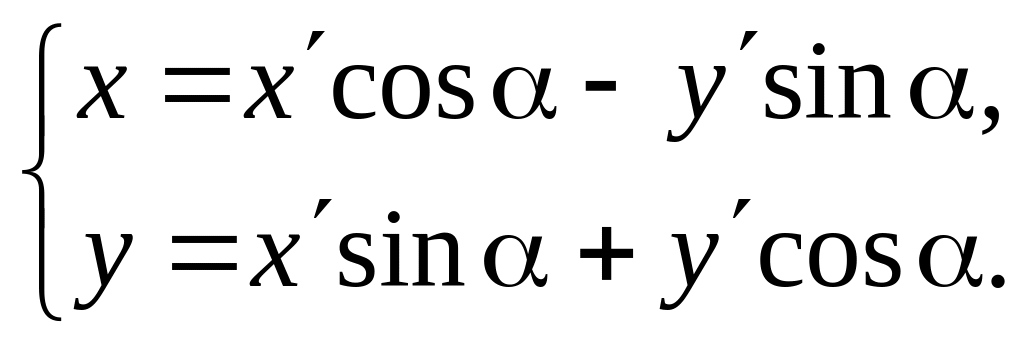

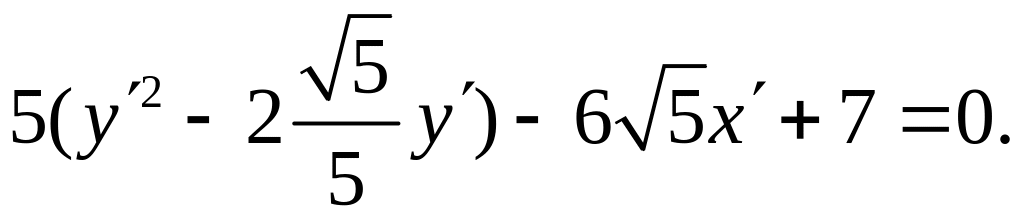
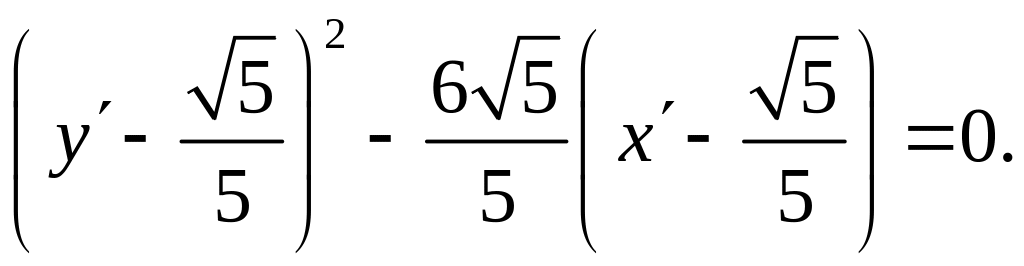
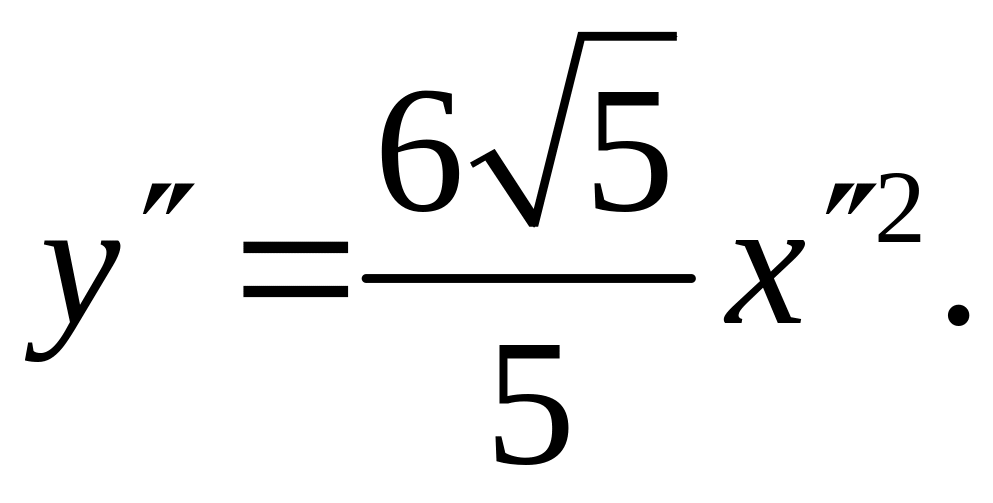
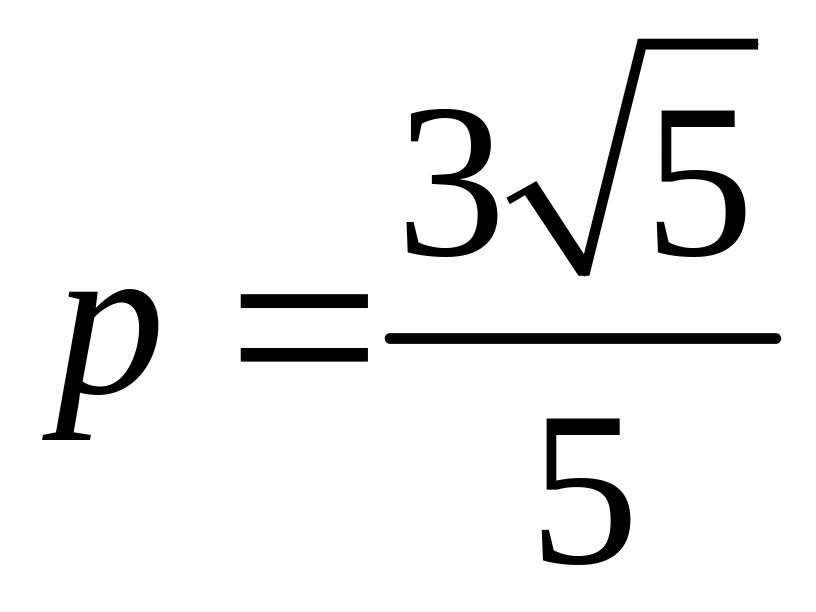 и с вершиной в начале координат системы
ху.
Парабола расположена симметрично
относительно оси х
и бесконечно простирается в положительном
направлении этой оси. Координаты
вершины в системе ху
и с вершиной в начале координат системы
ху.
Парабола расположена симметрично
относительно оси х
и бесконечно простирается в положительном
направлении этой оси. Координаты
вершины в системе ху
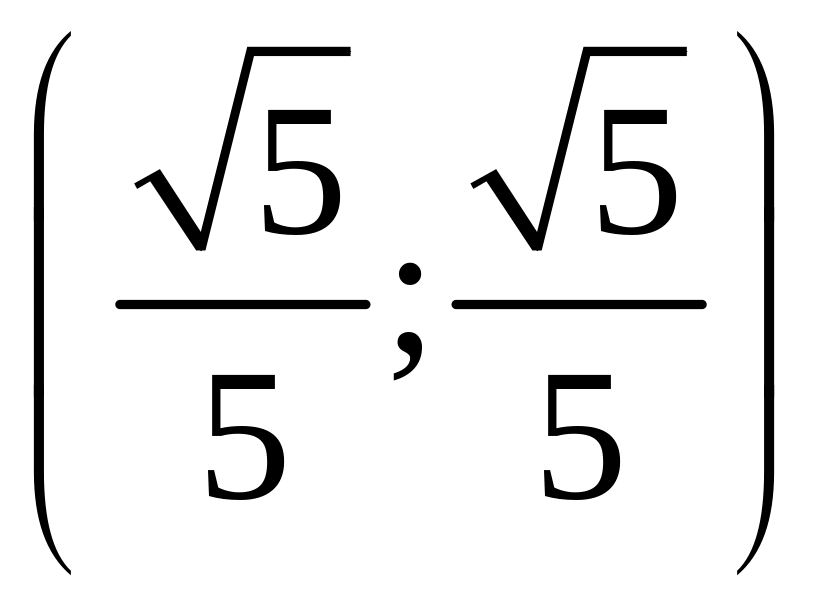 а в системе
ху
а в системе
ху

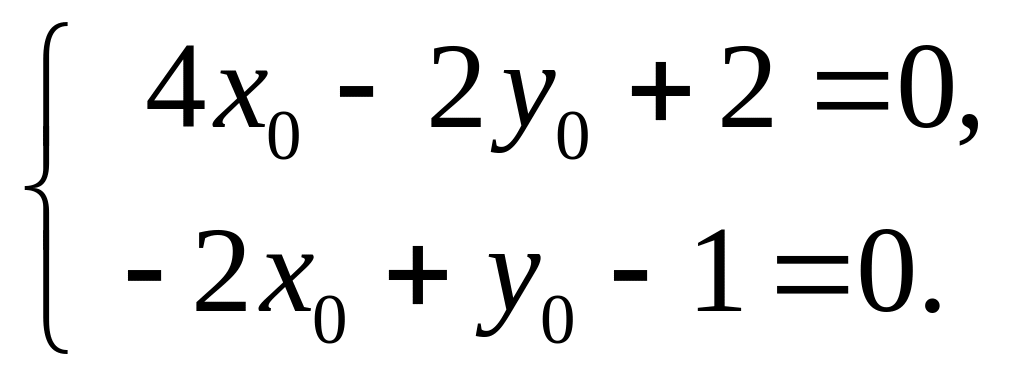

 так,
ось О1х
описывается уравнением
у
= -х + b, -1
= -2
+ b.
так,
ось О1х
описывается уравнением
у
= -х + b, -1
= -2
+ b. откуда
искомое уравнение параболы имеет вид:
х2
+ 2ху + у2
– 6х + 2у
+ 9
= 0.
откуда
искомое уравнение параболы имеет вид:
х2
+ 2ху + у2
– 6х + 2у
+ 9
= 0.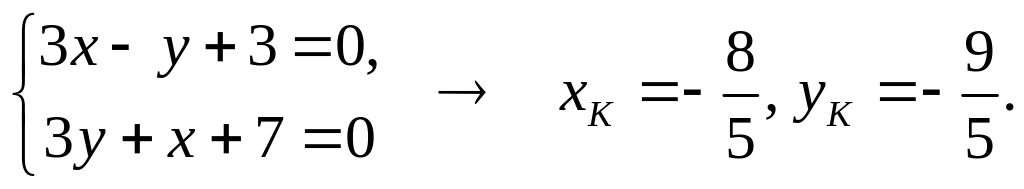
 позволяют найти КF
как расстояние от фокуса
позволяют найти КF
как расстояние от фокуса
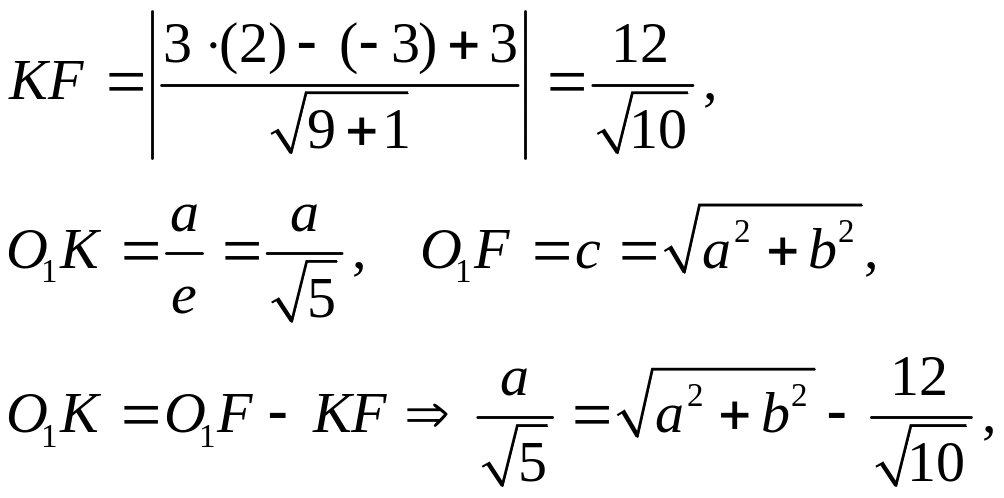 так
как
так
как
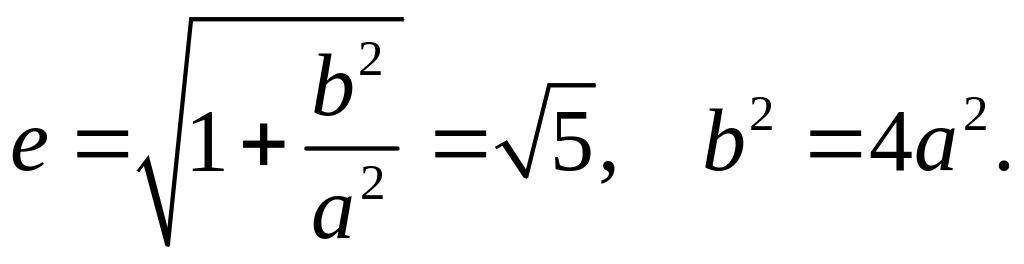 Значение а
находим из уравнения
Значение а
находим из уравнения
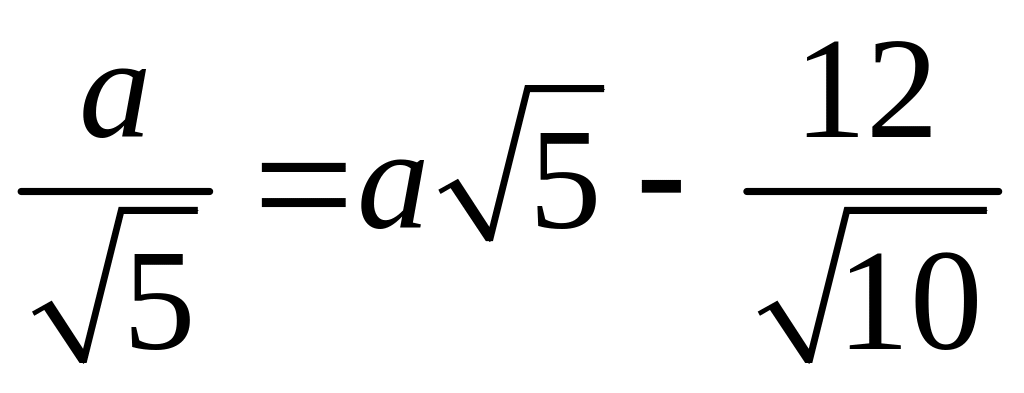 и получаем
и получаем