ПП_5_3_Ряды_Фурье

ПП5.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ. РЯДЫ ФУРЬЕ ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

5.3.1.Гармонический анализ. Основные положения

Гармоническим колебанием называется периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса.

Основной гармоникой называется простейшая периодическая функция вида y = f (x ) = a sin (ω x + ϕ0 )= a co s (ω x − ϕ0 ), где a – амплитуда, ω -

круговая частота, ϕ0 - начальная фаза колебания.

Если независимая переменная - время t , то величина y = f (t ) совершает

гармоническое колебание с периодом T =	2π	и частотой ν =		1	=	ω	.
	ω			T
						2π
Функции a2 sin (2ωx +ϕ0 ), a3 sin (3ωx +ϕ0 ), ...			называются высшими

гармониками относительно основной (второй, третьей, и т.д.).

Основная гармоника может быть представлена в виде суммы двух тригонометрических функций одного и того же аргумента:

a sin (ωx + ϕ0 )= a sin ωx cosϕ0 + a cos ωx sin ϕ0 = A sin ωx + B cos ωx .

Функции sin x и cos x являются периодическими с периодом T = 2π . Функции sin 2x и cos 2x , sin 3x и cos3x ,… также имеют период 2π . Любая линейная комбинация вида

a0 +a1 cos x +b1 sin x +a2 cos 2x +b2 sin 2x +...	(1)
также является периодической с периодом T = 2π .
Гармонический анализ используется для изучения	периодических

процессов. Любая величина f (t ), связанная с периодическим процессом,

по истечении периода T возвращается к своему первоначальному значению, т.е. является периодической функцией с периодом T .

Сущность гармонического анализа заключается в представлении функций, описывающих периодические процессы, в виде конечной или бесконечной суммы гармонических колебаний вида (1); гармонический анализ состоит в разложении периодических функций в сходящийся ряд Фурье.

5.3.2. Ортогональные системы функций

Предварительно укажем следующие утверждения, которые следует знать для дальнейшего изложения.

1)Интеграл от нечетной функции в симметричных пределах равен нулю. Если f (−x)= − f (x), то

∫a f (x)dx = 0 .

−a

2)f (−x)= f (x), f (x) – четная функция:

∫a f (x)dx =2∫a f (x)dx.

−a 0

1

3)Если функция f (x) имеет период 2π, то интеграл от нее по любому отрезку длины 2π имеет одно и то же значение, т.е.

a+∫2π	f (x)dx = 2∫π			f (x)dx.
a			0
Пусть функции	f1 (x)	и	f2 (x) заданы на отрезке x [a,b,], а произве-
дение этих функций	f1 (x)	f2 (x) интегрируемо на этом отрезке.
Функции f1 (x)	и f2 (x)			называются ортогональными на отрезке

[a,b], если ∫b f1 (x)f2 (x)dx =0.

a

Рассмотрим систему периодических тригонометрических функций с общим периодом 2π : {cos0 =1, cos x, sin x, cos 2x, sin 2x, ... cos nx, sin nx,... }.

Эти функции ортогональны на отрезке [−π, π], а значит, в силу утверждения 3) и на любом отрезке [a, a + 2π].

Интегралы:

				π∫sin nxdx =0,		π∫cos nxdx =0,	π∫cos mxsin nxdx = 0,
				−π	−π		−π
	при m ≠ n :			π∫ cos mx cos nx dx = 0	,	π∫sin mxsin nxdx =0 ,
				−π		−π
	при m=n:			π∫sin2 nx dx =π ;		π∫cos2 nx dx =π .
				−π		−π
	5.3.3. Тригонометрические ряды. Ряд Фурье
	Функциональный ряд вида:
		a0					∞
			+a1 cos x +b1 sin x + a2 cos 2x +b2 sin 2x +... = a0 + ∑(an cos nx +bn sin nx)
	2
						2	n=1

называется тригонометрическим рядом, а постоянные числа an , bn , (n =1, 2, 3...) называются коэффициентами ряда.

Коэффициенты Фурье и ряд Фурье для периодической функции с периодом 2π

Если: 1) f (x) – периодическая функция с периодом 2π;

2)f (x) интегрируема на интервале (−π ,π );

3)f (x) для всех x (−π ,π ) является суммой тригонометрического

			a0	∞
	ряда,	f (x)=		+ ∑(an cos nx +bk sin nx), равномерно сходящегося к
	f (x)	2		n=1	интервал (−π ,π ),
		на любом отрезке, вложенном в
	то для коэффициентов тригонометрического				ряда справедливы

2

	формулы Фурье:
	a0 =	1	π∫ f (x)dx, an =	1	π∫ f (x)cos nx dx, bn =	1	π∫ f (x)sin nx dx ;
		π				π
				π
			−π		−π		−π

числа an , bn называются коэффициентами Фурье функции f (x), а

тригонометрический ряд, коэффициентами которого служат эти числа, – рядом Фурье функции f (x).

Если функция f (x) разлагается в равномерно сходящийся триго-

нометрический ряд, то этот ряд является ее рядом Фурье.

5.3.4. Разложение функций в тригонометрические ряды

Вопрос о возможности разложения функции f(x) в тригонометрический ряд сводится к ответу на вопрос о том, какими свойствами должна обладать функция f (x), чтобы построенный для нее ряд Фурье сходился и

его сумма совпала с f (x).

В отличие от степенных рядов, в которые разлагаются только функции, имеющие производные всех порядков, в тригонометрические ряды разлагаются почти любые периодические функции.

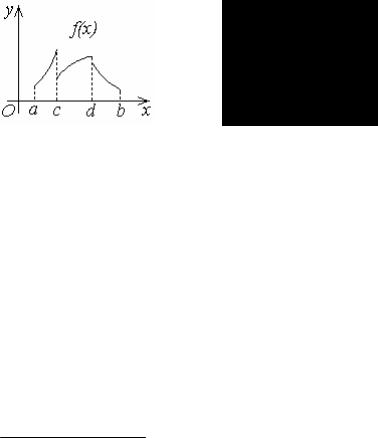
Функция f (x) называется кусочно-монотонной на отрезке [a,b], ес-

ли этот отрезок с помощью конечного числа точек x1, x2,…, xn-1 можно разбить на интервалы так, что на каждом из них функция f (x) непрерыв-

на и монотонна.

Кусочно-монотонная и ограниченная на [a,b] функция f (x) может иметь только конечное число

точек разрыва I рода.

Если в точке x=c имеет место разрыв, то в силу монотонности функции f (x) слева от точки с суще-

ствует предел lim f (x)= f (c −0), а в силу монотон-

x→c−0

ности справа существует предел lim f (x)= f (c +0).

x→c+0

Достаточные условия разложимости функции в ряд Фурье. Теорема Дирихле.

Если функция f (x) с периодом 2π ограничена и кусочномонотонна на отрезке [−π,π], то ряд Фурье, построенный для f (x), схо-

дится во всех точках этого интервала. При этом:

1) сумма S(x) этого ряда равна f (x) в точках непрерывности функции f (x);

2) если точка х = с является точкой разрыва f (x), то сумма ряда Фурье

S (c)= f (c +0)+ f (c −0). 2

3

5.3.4.1. Разложение в ряд четных и нечетных функций с периодом 2π

Пусть f (x) – периодическая функция с периодом 2π.

1). Если функция f (x) нечетная, f (−x)= − f (x), ее ряд Фурье содер-

∞

жит только синусы кратных дуг: f (x)= ∑bn sin nx.

n=1

2). Если функция f (x) четная, f (−x)= f (x), ее ряд Фурье содержит

a0

∞

только косинусы кратных дуг:

f (x)=

+ ∑an cos nx.

2

n=1

5.3.4.2. Ряд Фурье для функции с произвольным периодом Т=2l

Если

f (x + 2l )= f (x), то

f (x)=

a

∞

nπ

x +bn sin

nπ

0 + ∑ an cos

l

l

x ,

2

n=1

где

a =1 l

f

(x)dx;

a =1 l

f (x)cos n π x dx;

b

=

1

l

f (x)sin

nπ

x dx;

0

l −∫l

n

l −∫l

l

n

l −∫l

l

	S (π )= S (−π )=	f (π +0)+ f (π −0)	.
		2

5.3.4.3. Разложение в ряд Фурье непериодических функций

Сумма ряда Фурье есть периодическая функция, поэтому непериодическую кусочно-монотонную, заданную на интервале (−∞,∞) функцию

нельзя представить рядом Фурье. Но можно разложить ее в ряд Фурье, периодически продолжив, для любого конечного промежутка.

Для функции f (x)

построим функцию ϕ(x)

такую, что ϕ(x)= f (x) для x (−l; l ), а на всю действительную ось она

продолжается периодически с периодом 2l :

ϕ(x)=ϕ(x + 2l ).

4

Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ± l выполняется:

			S (l )=	ϕ(l −0)+ϕ(l + 0)		,
			2
	где	ϕ(l −0)= f (l −0), ϕ(l +0)=ϕ(−l +0)= f (−l +0),
	то есть	S (l )=	f (l −0)+ f (−l +0)		, S (−l )= S (l ).
			2				(0,l ), ее мож-
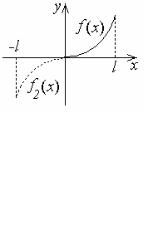
	Если произвольная функция f (x) задана на интервале

но представить в виде периодической функции ϕ(x) с периодом 2l , дополнив (продолжив) f (x) произвольным образом некоторой кусочномонотонной функцией f1 (x) на интервал (−l,0) так, что:

f (x), x (0, l );

ϕ(x)= f1 (x), x (−l, 0).

Так как продолжение f1 (x) первоначально заданной функции f (x) может быть выбрано бесчисленным множеством способов, то существует

бесчисленное множество рядов Фурье, которые сходятся к

f (x)

в интер-

вале (0,l ).

f (x) выберем четное и нечетное

Среди

различных продолжений

продолжения,

в результате которых получатся разложения

f (x)

либо по

косинусам, либо по синусам кратных дуг соответственно.

1.

Если f1 (x)= f (−x),

x (−l, 0),

f (x)

= a0

∞

то

+ ∑an cos nπx,

2

n=1

l

где an =

2 l

f (x)cos

nπx

dx, x (0, l ),

n =1, 2,...

l ∫0

l

2.

Если f1 (x)= − f (−x),

x (−l, 0),

∞

nπ x

то

f (x)

= ∑bn sin

,

n=1

l

b

=

2

l f (x)sin

nπx

dx,

x (0, l )

n

l ∫0

l

5.3.5. Комплексная форма ряда Фурье

∞

inπx

Ряд Фурье для функции

f (x) с периодом 2l имеет вид: f (x)= ∑cne l ,

n=−∞

1

l

inπ x

где cn =

f (x)e−

dx , n = 0, ±1, ±2, ... , (номер n считается не нату-

l

2l

−∫l

5

ральным, а целым числом).

Эта сумма называется рядом Фурье в комплексной форме, слагающие ее

	inπx
функции	c e l	– комплексными гармониками, коэффициенты
	n

cn – комплексными амплитудами гармоник.

5.3.6. Интеграл Фурье

Если непериодическая функция задана на всей числовой оси (−∞;∞), на любом конечном отрезке [−l;l] удовлетворяет условиям теоремы Дирихле и

∞

абсолютно интегрируема на всей числовой оси, т.е. ∫ f (x) dx = M < ∞,

−∞

то она может быть разложена в интеграл Фурье:

f (x)=

1

∞∫dk ∞∫

f (t )cos k

(x −t )dt .

π

0

−∞

Эта формула называется формулой Фурье, а интеграл, стоящий в

правой части, – интегралом Фурье. Функция F (k )

называется спек-

тральной плотностью.

f (x) с периодом

2l набор величин

Для

периодической функции

D =

a

2 +b 2

показывает, в какой мере в разложении функции f (x)

n

n

n

представлены различные гармоники cos

nπ x

, sin

nπx

и называется спек-

l

l

тром функции f (x). Для периодической функции f (x) спектр - функция

целочисленного аргумента, т.е. последовательность, величины отдельных членов которой показывает вклад соответствующих гармоник ( f (x) со-

ставляется как сумма бесконечного, но счетного количества гармоник). Для непериодической функции f (x) в разложении ее на простейшие

периодические составляющие присутствует несчетное количество слагаемых (интеграл), величина F (k )∆k описывает вклад гармоник с волно-

выми числами из интервала (k − ∆2k ;k + ∆2k ).

Интеграл Фурье можно представить в виде, подобном ряду Фурье:

				∞	(A(k )cos kx + B (k )sin kx)dk ,
		f (x)= ∫
				0
		A(k)=	1	∞	(t)coskt dt, B(k)=	1	∞
	где			∫ f			∫ f (t)sin kt dt ,
			π			π
				−∞			−∞

и амплитуды D (k )= A2 (k )+ B2 (k ).

6

ПП5.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ. РЯДЫ ФУРЬЕ

ПП5. 3.2. Ортогональные системы функций

Докажите соотношения:

1)

π∫sin nxdx = 0, 2)

π∫cos nxdx = 0,

−π

−π

3)

π∫cosmxsin nxdx =0,

−π

π

4)

∫ cos mx cos nxdx = 0 ,

при m ≠ n :

−π

π

5)

∫sin mx sin nxdx = 0 ,

−π

π

6)

∫sin2 nx dx =π,

при m=n:

−π

π

7)

∫cos2 nx dx =π.

−π

ДОКАЗАТЕЛЬСТВО.

π

ПП 5.№72.

1)

π∫

sin nx dx = −

cos nx

= 0 в силу нечетно-

−π

n

−π

сти подынтегральной функции.

2)

π∫

cosnx dx = sin nx

π

=

1 (sinπn −sin (−πn))=0 ,

−π

n

−π

n

так как sinπn = 0 .

3)

π∫cos mx sin nx dx =

−π

(

)

(

)

1

=

sin nxcosmx =

sin

m+n

x +sin

m−n

x =

2

=1 π∫(sin (n +m)x +sin (m −n)x)dx = 0 2 −π

всилу нечетности подынтегральной функции.

	4) при m ≠ n		π∫cos nx cos mx dx =
			−π				(	)	(	)
				1
	=	cosnxcosmx =				cos		n+m x+cos		n−m x		=
				2
							7

=1 π∫ (cos (n − m )x + cos (n + m )x )dx =

2 −π

=

1

sin (n − m)x

+

sin (n + m)x

π

= 0 .

2

n − m

n + m

−π

π∫sin nx sin mx dx =

5) при m ≠ n

−π

(

)

(

)

1

=

sin nxsin mx =

cos

n −m x −cos

n +m x

=

2

=1 π∫ (cos (n − m )x − cos (n + m )x )dx =

2 −π

1

sin

(

n −m

)

x

sin

(

n +m

)

x

π

=

−

= 0.

2

n −m

n +m

−π

6)

π∫sin2 nx dx =

1

π∫(1 −cos 2nx)dx =

−π

2−π

1

sin 2nx

π

1

(π +π )=

=

x −

=

π .

2

2n

2

−π

7)

π∫ cos2 nx dx =

1

π∫ (1 + cos 2nx)dx =

−π

2−π

1

sin 2nx

π

1

(π +π )=

=

x +

=

π .

2

2n

2

−π

ПП 5. 3.4. Разложение функций в тригонометрические ряды

Разложите в ряд Фурье периодическую функцию с периодом 2π, если

1,	x [0, π]		.
f (x)=		x (π,2π]
−1,

ПП 5.№73.

РЕШЕНИЕ:

Вместо промежутка [0; 2π] будем рассматривать промежуток [−π;π]. Коэффициенты Фурье:

4 ∑∞ sin (2n +1)x π n=0 2n +1

8

an = π1 π∫ f (x)cos nx dx = 0 , n = 0,1,2,...,

−π

так как подынтегральная функция нечетна;

bn =

1

π∫

f (x)sin nx dx =

π

−π

1

0

π

=

∫(−1)sin nx dx +

∫sin nx dx

=

π

−π

0

=

1

cos nx

0

−cos

nx

π

=

2

(cos 0

−cos nπ )=

π

n

n

πn

−π

0

0, если п = 2k − четное;

=4 , если п = 2k +1− нечетное.

πn

Разложение

f (x)

в ряд Фурье имеет вид:

f (x)= 4

sin x + sin 3x + sin 5x +... = 4 ∑sin (2n +1)x.

∞

π 1

3

5

π

n=0

2n +1

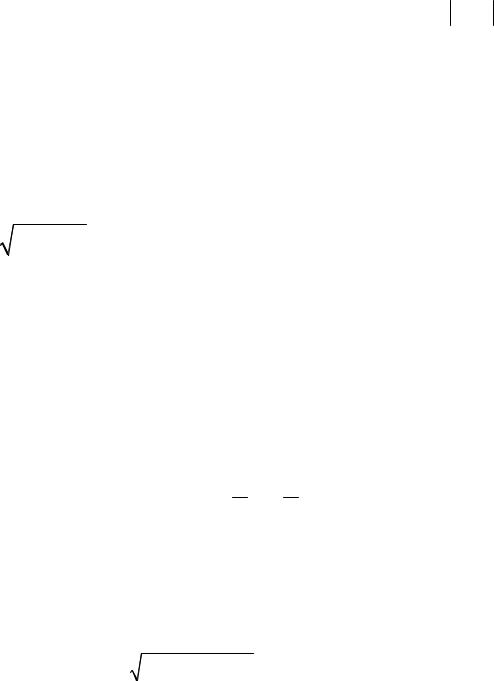
Построим графики трех первых частичных сумм ряда.

С увеличением числа слагаемых частичная сумма все точнее представляет f (x).

Полученное разложение может быть исполь-

зовано для приближенного вычисления числа

π : подставляя в разложение

x = π получаем:

(−1)

n

2

π

∞

=1− 1 + 1 − 1

= ∑

+....

4

2n +1

n=0

3 5 7

Разложите в ряд Фурье периодическую

k

ПП 5.№74. функцию с периодом 2π, если на отрезке

π

cos2

kx

2

+ 4∑(−1)

∞

[−π,π] она задана формулой

f (x)= x2 .

3

k =1 k

9

РЕШЕНИЕ: Коэффициенты Фурье:

bn = 0 в силу четности разлагаемой функции функции;

1 π

2

1

x3

π

2π

2

a0 =

−∫π

x

dx =

=

,

π

π

3

−π

3

an =

1

π∫

x2 cos nxdx =

π

−π

(интегрируем по частям)

u = x2 , dv = cos nxdx

=

du = 2xdx, v =

sin nx

n

1

x2 sin nx

π

2

π

=

−

xsin nx dx

=

π

n

n

−∫π

(еще раз ин-

−π

тегрируем по частям)

u= x, dv =sin nx dx

=du = 2xdx, v = −cosnnx =

2

x cos nx

π

1

π

−

−

+

∫cosnx dx

=

nπ

n

n

−π

−π

4

,

еслиn = 2k − четное;

4

2

=

cos nπ = n

4

2

n

, если n = 2k +1 − нечетное.

−

n

2

Разложение в ряд Фурье имеет вид:

f

(x)=

π

2

cos x

cos 2x

cos 3x

−4

−

+

−...

=

3

1

2

2

3

2

π

2

∞

(−1)

k

cos

kx

=

+ 4∑

.

3

k

2

k =1

10