
- •9.16. Линейные однородные дифференциальные уравнения
- •I. Основные понятия теории дифференциальных уравнений.
- •III. Линейные дифференциальные уравнения первого порядка
- •Учебный модуль №9 «Дифференциальные уравнения» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Дифференциальные уравнения»
- •9.1. Физические задачи, приводящие к дифференциальным уравнениям
- •9.2. Основные понятия теории дифференциальных уравнений
- •9.3. Дифференциальные уравнения первого порядка. Задача Коши
- •9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •9.5. Однородные дифференциальные уравнения и приводящиеся к ним
- •9.6. Линейные дифференциальные уравнения первого порядка
- •9.7. Уравнение Бернулли
- •9.8. Дифференциальные уравнения в полных дифференциалах
- •9.9. Особые решения дифференциальных уравнений первого порядка
- •9.10. Модели прикладных задач с применением дифференциальных уравнений
- •9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
- •9.12. Дифференциальные уравнения, допускающие понижение порядка
- •9.13. Понятие о краевых задачах для обыкновенных дифференциальных уравнений
- •9.14. Линейные дифференциальные уравнения высших порядков
- •9.15. Линейные однородные дифференциальные уравнения, свойства их решений. Определитель Вронского. Условия линейной зависимости и независимости решений
- •9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
- •9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
- •Вопросы к экзамену по модулю №9
- •Дифференциальные уравнения в полных дифференциалах.
9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим дифференциальное уравнение второго порядка
![]() ,
,
где p и q – постоянные действительные числа. Чтобы найти общее решение этого уравнения надо найти два его линейно независимые частные решения.
Будем искать частные решения в виде
![]() ,
где
,
где
![]() ;
;
тогда
![]() ,
,
![]() .
Подставим
.
Подставим
![]() ,
,
в .
,
,
в .
![]()
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Если k
будет удовлетворять уравнению , то
![]() будет решением уравнения . Уравнение
называется характеристическим
уравнением,
соответствующим уравнению .
будет решением уравнения . Уравнение
называется характеристическим
уравнением,
соответствующим уравнению .
В зависимости от
дискриминанта приведенного квадратного
уравнения
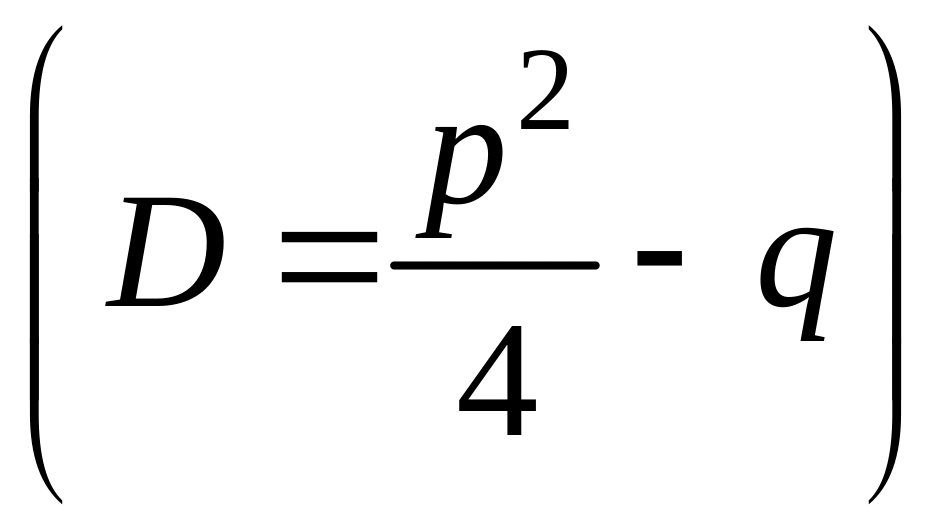 рассмотрим три случая.
рассмотрим три случая.
Корни характеристического уравнения действительны и различны
 :
:
 ,
,
 .
В этом случае частными решениями будут
функции
.
В этом случае частными решениями будут
функции
 и
и
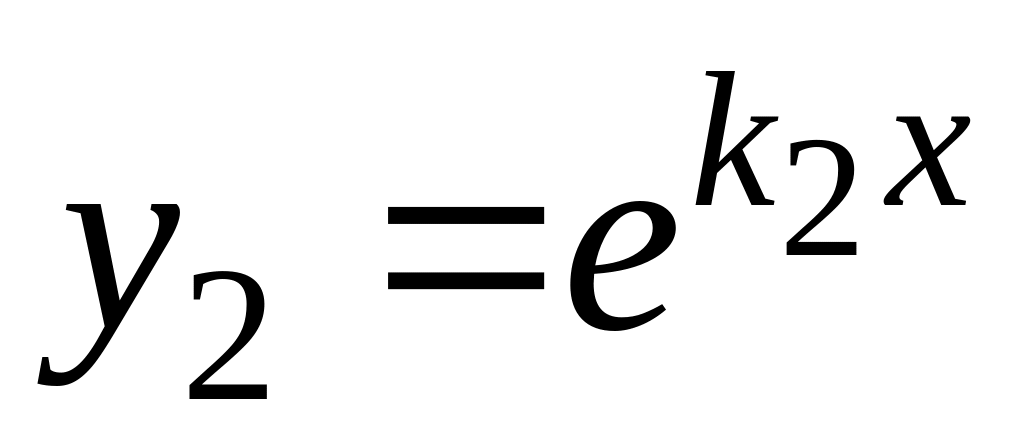 ,
причем они линейно независимы, так как
,
причем они линейно независимы, так как
 при
.
при
.
Следовательно, общее решение
![]() .
.
Пример
9.16.1. Решить
уравнение
![]() .
.
Решение. Характеристическое
уравнение имеет вид
![]()
![]() ,
,
![]() .
Тогда
.
Тогда
![]() – общее решение.
– общее решение.
Корни характеристического уравнения действительны и равны
 :
:
 .
.
Одно частное
решение
.
Будем искать второе частное решение в
виде
![]() ,
где
– неизвестная функция, подлежащая
определению.
,
где
– неизвестная функция, подлежащая
определению.
Дифференцируя, находим
![]() ,
,
![]() .
.
Подставляя
![]() ,
,
![]() ,
,
![]() в , получим
в , получим
![]() .
.
Так как k1
– корень , то
![]() .
Кроме того,
.
Кроме того,
 =
=![]() ,
так как дискриминант
,
так как дискриминант
![]() .
Из
.
Из
![]()
![]()
![]() .
.
Таким образом, от
уравнения остается
![]()
![]()
![]()
![]() .
Так как мы ищем частное решение
,
то можно положить
.
Так как мы ищем частное решение
,
то можно положить
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
Итак,
.
Итак,
![]() .
Это решение линейно независимо с первым,
так как
.
Это решение линейно независимо с первым,
так как
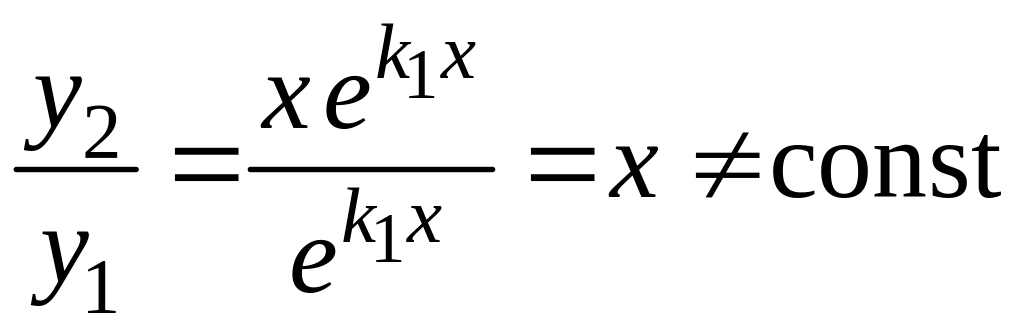 .
.
Поэтому общим решением будет функция
![]() ,
или
,
или
![]() .
.
Пример
9.16.2. Дано
уравнение
![]() .
.
Решение.
Запишем характеристическое уравнение
![]() ,
,
,
,
![]() ,
т.е
,
т.е
![]() .
(В данном случае в левой части мы имеем
полный квадрат
.
(В данном случае в левой части мы имеем
полный квадрат
![]()
![]()
![]() ,
,
![]() ;
,
;
,
![]() ).
Общим решением будет функция
).
Общим решением будет функция
![]() .
.
Корни характеристического уравнения комплексные
 .
.
Из известной формулы решения приведенного характеристического уравнения получаем
 .
.
Пусть действительная
часть
![]() ,
а мнимая
,
а мнимая

 ,
тогда
,
тогда
![]() ,
, ![]()
и частные решения можно записать в виде
![]() ,
,
![]() .
.
Это комплексные функции действительного аргумента и они нас не очень-то устраивают.
Докажем, что если
функция
![]() удовлетворяет уравнению , то этому
уравнению удовлетворяют и функции
и
.
удовлетворяет уравнению , то этому
уравнению удовлетворяют и функции
и
.
![]() ,
или
,
или
![]() .
.
Но комплексная функция равна нулю, если равны нулю действительная и мнимая части, т.е.
![]() ,
,
![]()
и являются решениями .
Функции представим по формуле Эйлера
![]() ,
, ![]() .
.
По доказанному
частными решениями уравнения будут
функции
![]() и
и
![]() ,
которые линейно независимы, так как
,
которые линейно независимы, так как
 .
.
Следовательно, общее решение уравнения
![]() , или
, или
![]() ,
,
где С1 и С2 произвольные постоянные.
Пример
9.16.3. Найти
частное решение уравнения
![]() ,
удовлетворяющее начальным условиям
,
,
удовлетворяющее начальным условиям
,
![]() .
.
Решение. Характеристическое
уравнение
![]()
![]()
![]() ,
т.е.
= 0,
= 3. Тогда
,
т.е.
= 0,
= 3. Тогда
![]() ,
т.е.
,
т.е.
![]() – общее решение данного уравнения.
– общее решение данного уравнения.
![]() .
.

т.е. частное решение
имеет вид
![]()
Используя формулы , и , можно решать линейные однородные дифференциальные уравнения высших порядков.
Рассмотрим в общем виде уравнение третьего порядка
![]() ,
,
где а1, а2, а3 – постоянные действительные числа. Соответствующее характеристическое уравнение, очевидно, имеет вид
![]() .
.
Рассмотрим следующие случаи:
 – действительные
числа. Тогда общее решение
– действительные
числа. Тогда общее решение
![]() .
.
 – действительные
числа. Тогда
– действительные
числа. Тогда
![]() .
.
 – действительные
числа. Тогда
– действительные
числа. Тогда
![]() .
.
k1 – действительный корень, k2,3 = i – комплексные корни.
![]()
(все остальные случаи входят в рассмотренные).
Пример
9.16.4. Найти
общее решение уравнения
![]() .
.
Решение. Составляем и решаем характеристическое уравнение
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() .
Поэтому
.
Поэтому
![]() – искомое общее
решение.
– искомое общее
решение.
