9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными

Переходим к изучению дифференциальных уравнений первого порядка, для которых известны способы нахождения их решений или интегралов. Одним из таких являются дифференциальные уравнения с разделяющимися переменными.

Дифференциальное уравнение вида

,

где правая часть есть произведение функции , зависящей только от x, на функцию , зависящую только от y, называют уравнением с разделяющимися переменными. Пусть . Тогда по правилу пропорции, поменяв местами и , получим

.

Интегрируя левую часть по y, а правую по x, получим общий интеграл данного уравнения .

В дальнейшем дифференциальное уравнение вида

будем называть дифференциальным уравнением с разделенными переменными (при имеется функция, зависящая только от x, а при  функция, зависящая только от y).

Его общий интеграл: .

Пример 9.4.1. Решить дифференциальное уравнение .

Решение. Это дифференциальное уравнение с разделенными переменными, поэтому . Пусть , тогда . Получили общий интеграл, геометрически представляющий собой семейство окружностей радиуса С с центром в начале координат.

Уравнение вида

называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметричной форме.

Если и для любых x и y из области существования решения, то, разделив обе части уравнения на

, получим дифференциальное уравнение с разделенными переменными

.

Используя свойство инвариантности дифференциала, проинтегрируем равенство . В результате получим выражение

,

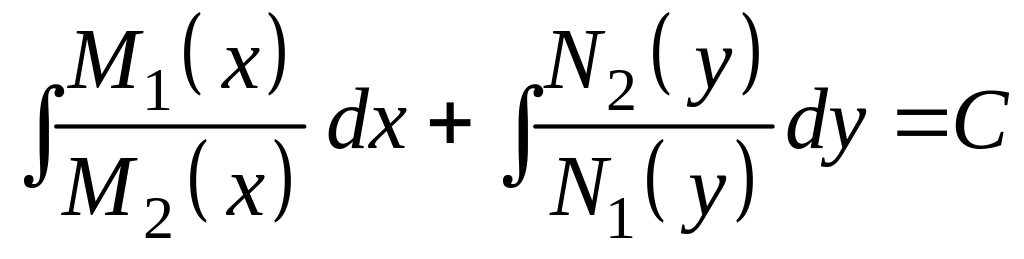являющееся общим интегралом дифференциального уравнения .

В тех точках, где или могут появиться другие решения уравнения . В самом деле, если x = x₁ – корень уравнения , то, положив в x = x₁, получим тождество

,

поскольку и . Следовательно, x = x₁ – решение уравнения . Аналогично, если y₁ – корень уравнения , то y = y₁ – решение уравнения .

Пример 9.4.2. Решить уравнение .

Решение. Разделим обе части на произведение . Тогда (в этом примере константу удобно выбрать в виде ln C). Отсюда получаем , тогда  общее решение данного уравнения. Кроме него решениями этого уравнения являются функции x = 0 и y = 0.

К уравнениям с разделяющимися переменными приводятся уравнения вида

.

Введем замену . Тогда , а (предполагаем ) и уравнение принимает вид

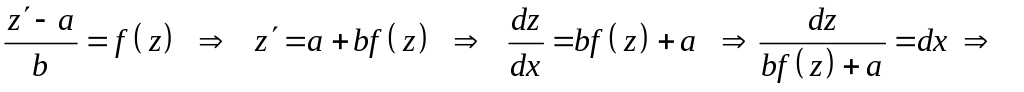
. После взятия интеграла необходимо вместо z подставить .

Если b=0, получаем уравнение , которое является уравнением с разделенными переменными,

.

9.5. Однородные дифференциальные уравнения и приводящиеся к ним

Определение 9.5.1. Функция называется однородной n-го порядка относительно переменных x и y, если при справедливо тождество .

Пример 9.5.1. Функция есть однородная функция второго порядка, так как

.

Пример 9.5.2. Функция есть однородная функция нулевого порядка, так как

.

Определение 9.5.2. Дифференциальное уравнение первого порядка

называется однородным, если функция есть однородная функция нулевого порядка относительно x и y.

По условию . Положив в этом тождестве , получим , т.е. однородная функция нулевого порядка зависит только от отношения аргументов. Уравнение принимает вид

.

Сделаем подстановку , т.е. y = zx. Тогда . Подставляя в , получим

.

Это уравнение с разделяющимися переменными.

.

Подставляя после интегрирования , получим общий интеграл уравнения , а значит, и уравнения .

Пример 9.5.3. Решить уравнение .

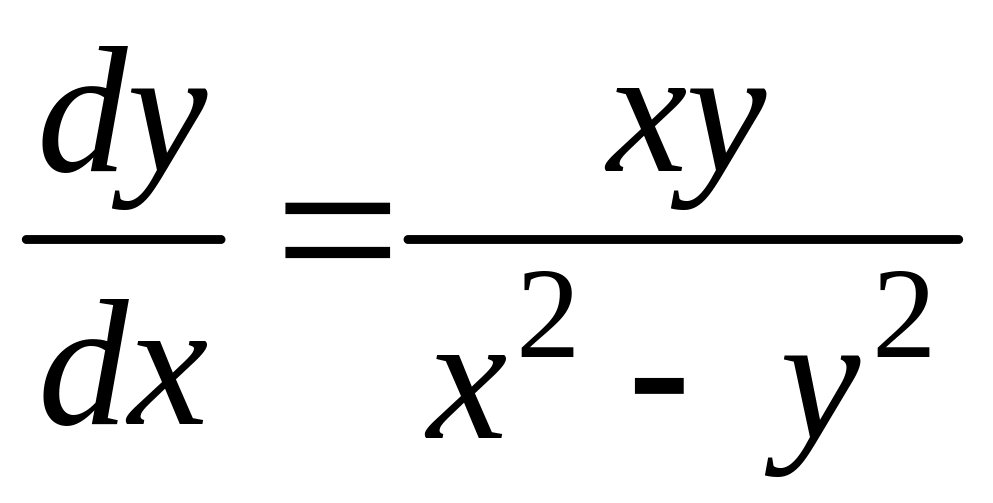Решение. В правой части имеется однородная функция нулевого порядка, так как . Пусть , y = zx, и наше уравнение принимает вид

. Отсюда, интегрируя, получаем   . Подставляя , получим общий интеграл исходного уравнения .

Замечание. Дифференциальное уравнение вида

будет однородным в том и только том случае, когда и являются однородными функциями одного и того же порядка.

Действительно, из уравнения . Тогда . Уравнение можно решать подстановкой y = zx, dy = zdx + xdz, не приводя его к виду .

Рассмотрим далее дифференциальные уравнения, приводящиеся к однородным.

К однородным уравнениям сводятся уравнения вида

,

где a₁, b₁, c₁, a₂, b₂, c₂ – постоянные числа.

Для этого введем новые переменные t и S вместо x и y по формулам

, ,

где  и  – некоторые числа.

Тогда dx= dt, dy = dS, и уравнение принимает вид



.

Подберем числа  и  так, чтобы уравнение стало однородным. Для этого достаточно потребовать выполнение системы равенств:

Если определитель , то система имеет единственное решение  и , при котором уравнение становится однородным, и которое решается подстановкой . После решения необходимо вернуться к х и у по формулам , .

Если , то, положив , получим , и тогда исходное уравнение принимает вид , т.е. имеет вид , которое подстановкой сводится к дифференциальному уравнению с разделяющимися переменными, как было показано в 9.4.

Если же , то , , и уравнение принимает вид

, , ,

где . Тогда – общее решение .

Примеры решения таких уравнений показаны в практической части модуля.