
- •9.16. Линейные однородные дифференциальные уравнения
- •I. Основные понятия теории дифференциальных уравнений.
- •III. Линейные дифференциальные уравнения первого порядка
- •Учебный модуль №9 «Дифференциальные уравнения» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Дифференциальные уравнения»
- •9.1. Физические задачи, приводящие к дифференциальным уравнениям
- •9.2. Основные понятия теории дифференциальных уравнений
- •9.3. Дифференциальные уравнения первого порядка. Задача Коши
- •9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •9.5. Однородные дифференциальные уравнения и приводящиеся к ним
- •9.6. Линейные дифференциальные уравнения первого порядка
- •9.7. Уравнение Бернулли
- •9.8. Дифференциальные уравнения в полных дифференциалах
- •9.9. Особые решения дифференциальных уравнений первого порядка
- •9.10. Модели прикладных задач с применением дифференциальных уравнений
- •9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
- •9.12. Дифференциальные уравнения, допускающие понижение порядка
- •9.13. Понятие о краевых задачах для обыкновенных дифференциальных уравнений
- •9.14. Линейные дифференциальные уравнения высших порядков
- •9.15. Линейные однородные дифференциальные уравнения, свойства их решений. Определитель Вронского. Условия линейной зависимости и независимости решений
- •9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
- •9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
- •Вопросы к экзамену по модулю №9
- •Дифференциальные уравнения в полных дифференциалах.
9.7. Уравнение Бернулли
Рассмотрим уравнение вида
![]() ,
,
где и - непрерывные функции от х (или постоянные), а n 0 и n 1 (в противном случае получилось бы линейное уравнение). Это уравнение, называемое уравнением Бернулли, приводится к линейному следующим преобразованием.
Разделив обе части
уравнения на
![]() ,
получим
,
получим
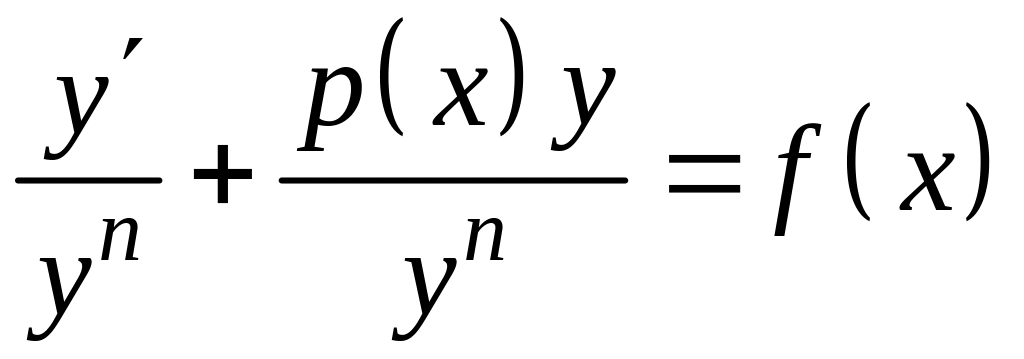 ,
или
,
или
![]() .
.
Сделаем, далее,
замену
![]() .
.
Умножим обе части
уравнения на
![]() .
.
![]()
![]() ,
,
т.е. получили
линейное дифференциальное уравнение
относительно z
и
![]() .
Найдя его общий интеграл и подставив
.
Найдя его общий интеграл и подставив
![]() ,
получим общий интеграл уравнения
Бернулли.
,
получим общий интеграл уравнения
Бернулли.
Пример
9.7.1. Найти
общее решение дифференциального
уравнения
![]() .
.
Решение. Предполагая
х
0, разделим
обе части дифференциального уравнения
на х,
тогда
![]() является уравнением Бернулли, где
является уравнением Бернулли, где
![]() .
Умножим обе части уравнения на
.
Умножим обе части уравнения на
![]() ,
в результате имеем
,
в результате имеем
 .
.
Сделаем подстановку
![]()
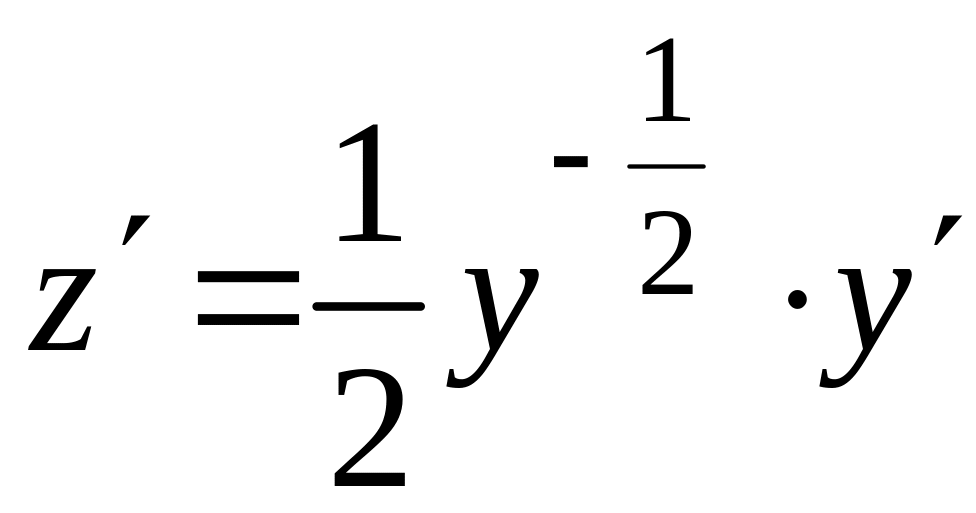 .
Умножая обе части последнего
дифференциального уравнения на
.
Умножая обе части последнего
дифференциального уравнения на
![]() ,
получим
,
получим
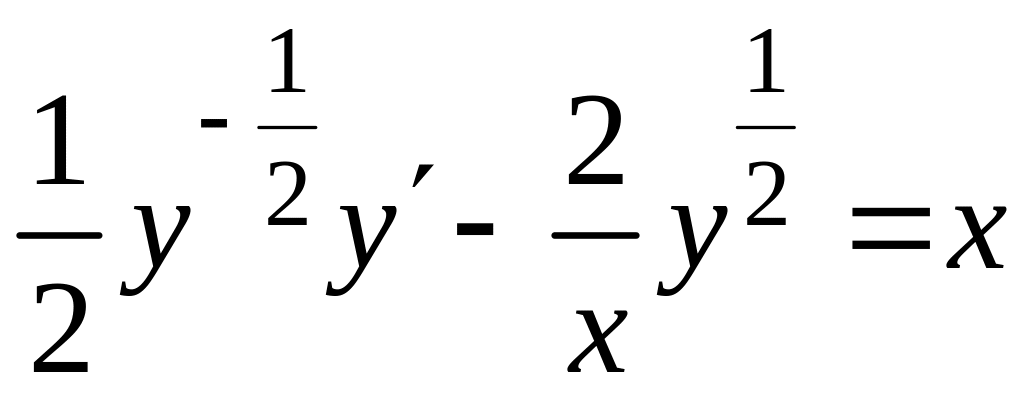 ,
,
![]() ,
а это уже линейное дифференциальное
уравнение относительно z
и
.
Найдем его общее решение по формуле ,
взяв
,
а это уже линейное дифференциальное
уравнение относительно z
и
.
Найдем его общее решение по формуле ,
взяв
![]() ,
f(x)
= x.
,
f(x)
= x.
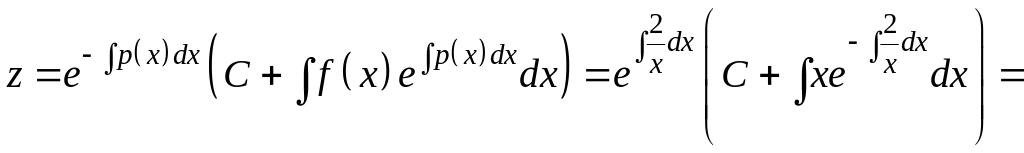
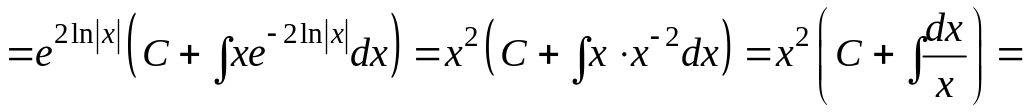
![]() .
.
Так как
,
то
![]()
![]() – искомое общее решение.
– искомое общее решение.
Замечание. Дифференциальное уравнение можно сразу решать методом Бернулли или Лагранжа, не сводя его к линейному.
Пример
9.7.2. Решить
уравнение
![]() .
.
Решение. Это
уравнение Бернулли. Решение будет искать
в виде
![]()
.
Исходное уравнение принимает вид
.
Исходное уравнение принимает вид
![]()
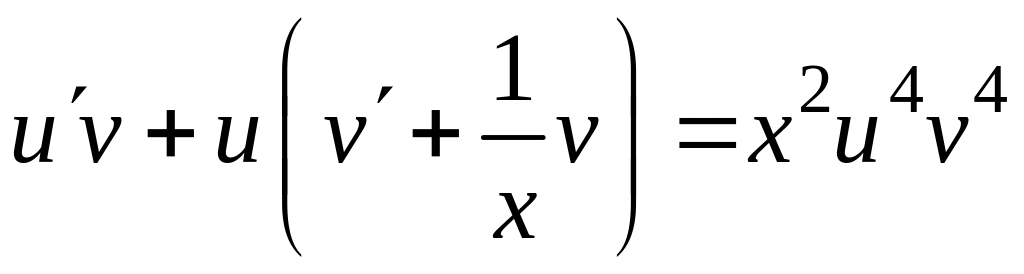 .
.
Выберем функцию
v(x)
таким образом, чтобы
![]() .
В результате получаем систему:
.
В результате получаем систему: 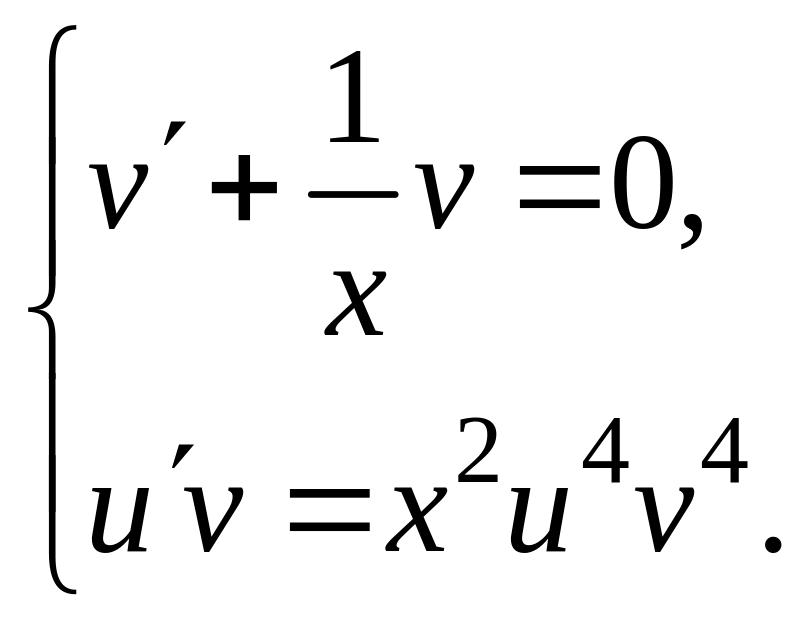
Решим первое
уравнение системы
![]()
![]()
![]()
![]()
![]() .
Тогда второе уравнение системы
.
Тогда второе уравнение системы
![]() принимает вид
принимает вид
![]()
![]()
![]()
![]()
![]()
![]()
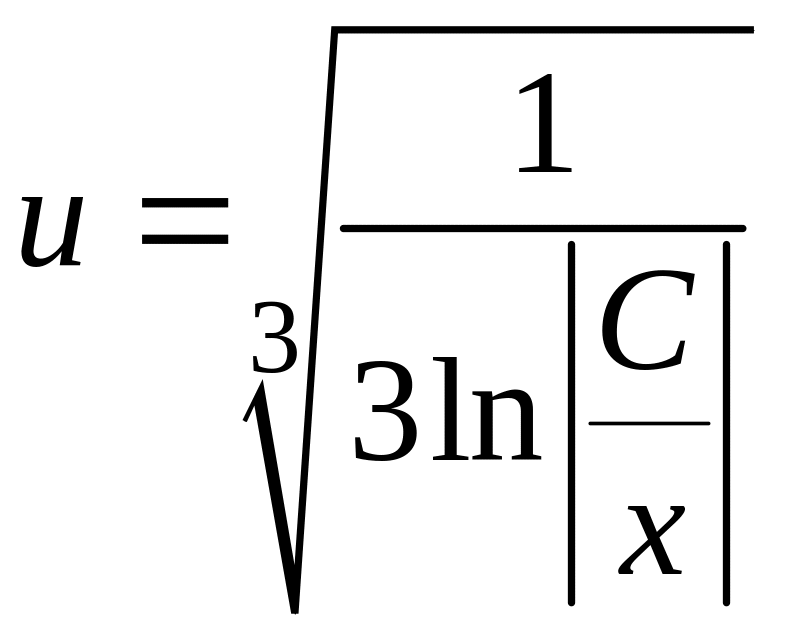 .
Итак,
,
т.е.
.
Итак,
,
т.е.
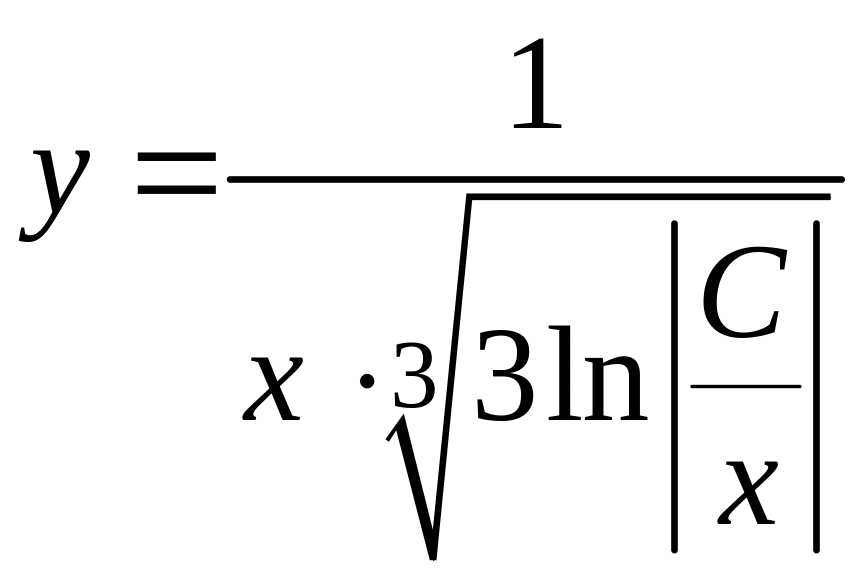 будет общим решением исходного уравнения.
будет общим решением исходного уравнения.
9.8. Дифференциальные уравнения в полных дифференциалах
Напомним, что
полным дифференциалом функции двух
переменных
![]() называется выражение
называется выражение
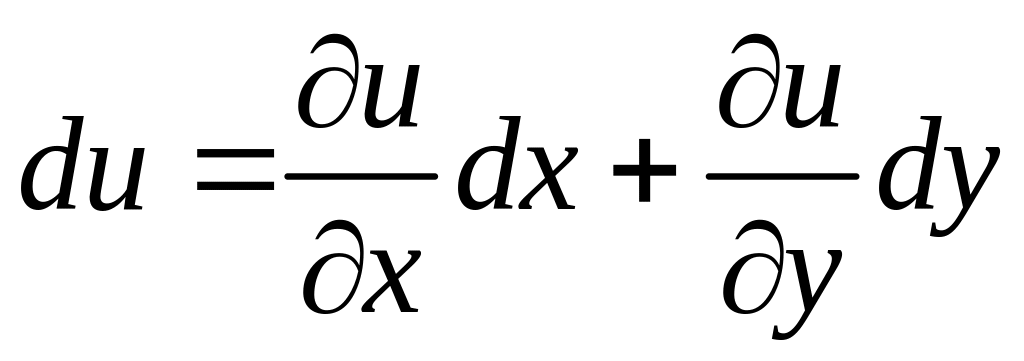 .
.
Уравнение
![]()
называется
дифференциальным уравнением в полных
дифференциалах, если его левая часть
представляет собой полный дифференциал
некоторой функции
![]() ,
т.е.
,
т.е.
![]() .
В этом случае
уравнение можно записать в виде
.
В этом случае
уравнение можно записать в виде
![]() ,
откуда следует, что соотношение
,
откуда следует, что соотношение
![]()
является его общим интегралом.
Теорема
9.8.1. Пусть
![]() и
и
![]() – функции, непрерывные в некоторой
односвязной (не имеющей «дырок» внутри
себя) области D
плоскости XOY
и имеющие
в ней непрерывные частные производные
– функции, непрерывные в некоторой
односвязной (не имеющей «дырок» внутри
себя) области D
плоскости XOY
и имеющие
в ней непрерывные частные производные
![]() и
и
![]() .
Тогда, для того, чтобы выражение
.
Тогда, для того, чтобы выражение
![]()
было полным дифференциалом некоторой функции , необходимо и достаточно, чтобы во всех точках области D было выполнено условие:
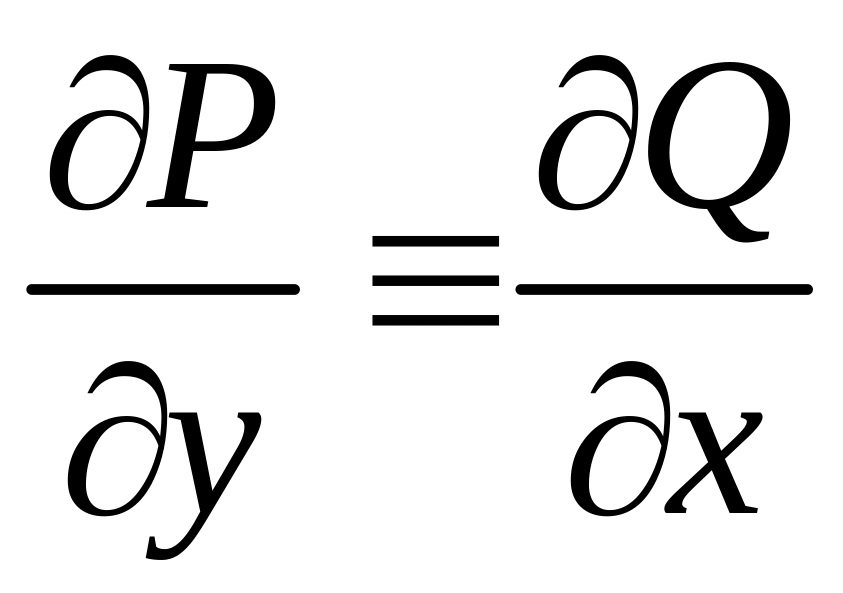 .
.
Доказательство.
Необходимость. Пусть выражение является полным дифференциалом некоторой функции , т.е.
 .
Отсюда
.
Отсюда
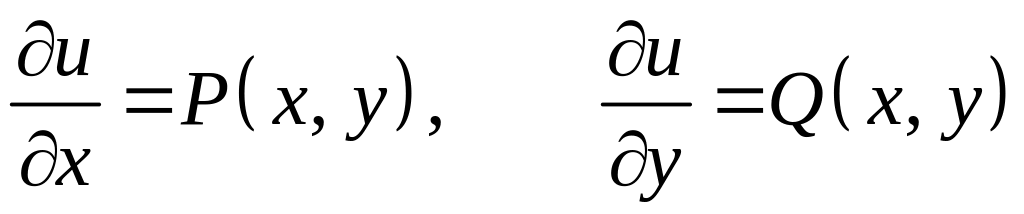 .
.
Дифференцируя
первое из этих равенств по y,
а второе – по x,
получим 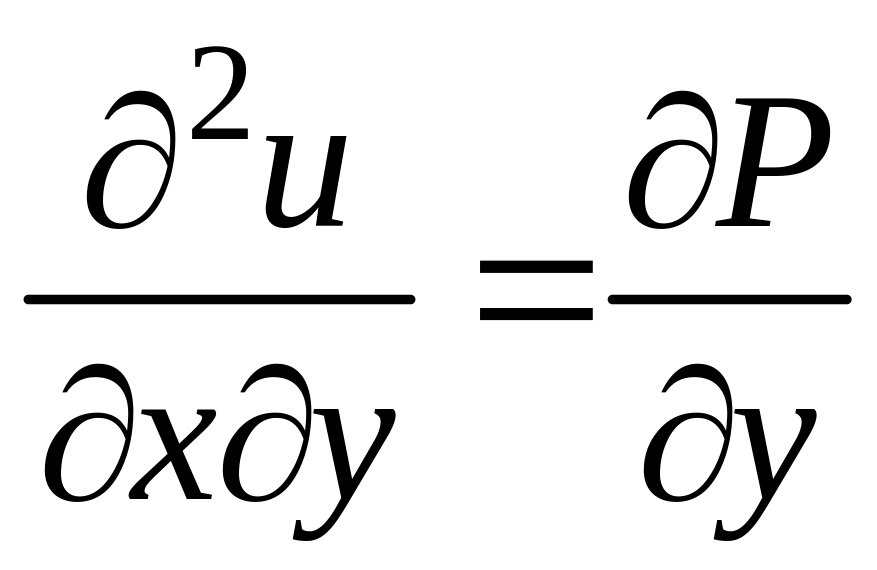 ,
, 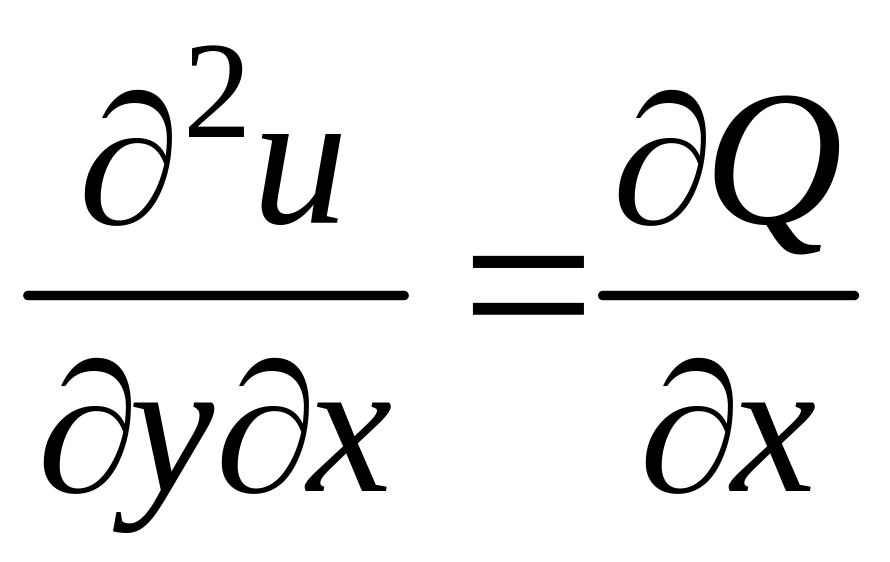 ,
откуда по теореме о равенстве смешанных
производных получаем
.
,
откуда по теореме о равенстве смешанных
производных получаем
.
Достаточность. Покажем, что при выполнении условия выражение есть полный дифференциал некоторой функции .
Из соотношения
![]() находим
находим
 ,
,
где x0 – абсцисса любой точки из области существования решения.
При интегрировании
по x
мы считаем y
постоянным и поэтому произвольная
постоянная интегрирования может зависеть
от y.
Подберем
![]() так, чтобы выполнялось второе из
соотношений . Для этого продифференцируем
обе части последнего равенства по y
и результат приравняем
:
так, чтобы выполнялось второе из
соотношений . Для этого продифференцируем
обе части последнего равенства по y
и результат приравняем
:
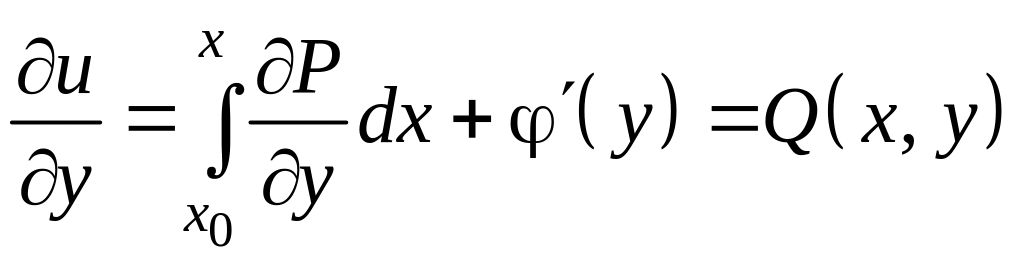 .
.
Но, так как
 ,
то
,
то  ,
т.е.
,
т.е.
![]() ,
или
,
или ![]() .
.
Следовательно,
![]() ,
или
,
или
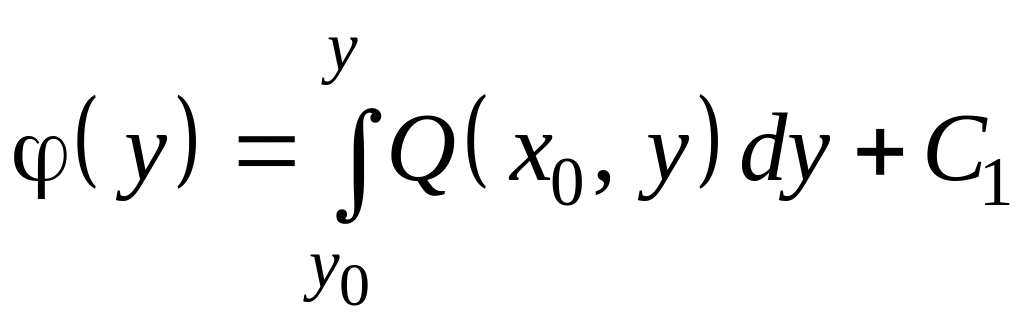 .
.
Таким образом, функция будет иметь вид
 ,
,
где точка – точка, в окрестности которой существует решение уравнения .
Если при построении функции брать за исходное второе из равенств , то получим, что
 .
.
В формулах и
нижние пределы интегрирования нужно
выбирать так, чтобы получающиеся
интегралы имели смысл. Удачный выбор
![]() и
и
![]() во многих случаях облегчает задачу
интегрирования уравнения.
во многих случаях облегчает задачу
интегрирования уравнения.
Напомним, что общим интегралом уравнения будет (произвольные постоянные С1 или С2 можно включить в постоянную С).
Пример
9.8.1. Решить
уравнение
 .
.
Решение. Проверяем,
не есть ли это уравнение в полных
дифференциалах. Пусть
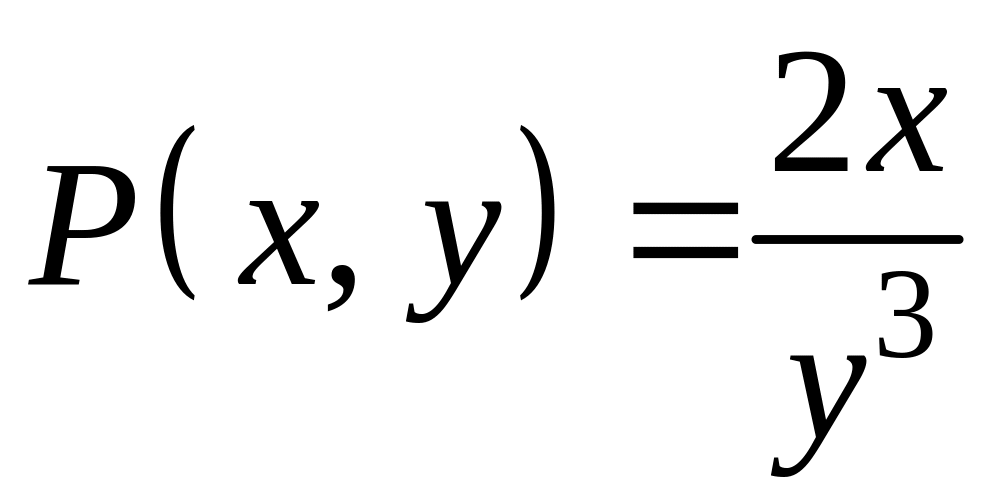 ,
,
 ,
тогда
,
тогда
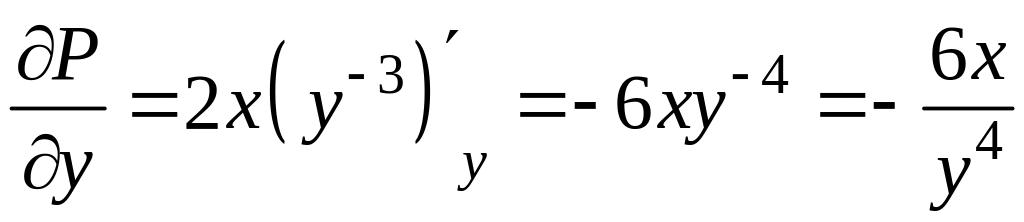 ;
; 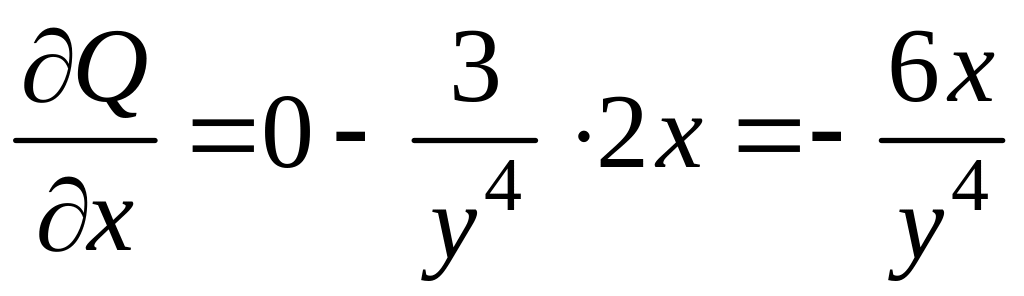 .
Условие при y
0 выполняется. Значит, левая часть
данного уравнения есть полный дифференциал
некоторой неизвестной функции
.
Найдем эту функцию.
.
Условие при y
0 выполняется. Значит, левая часть
данного уравнения есть полный дифференциал
некоторой неизвестной функции
.
Найдем эту функцию.
Так как 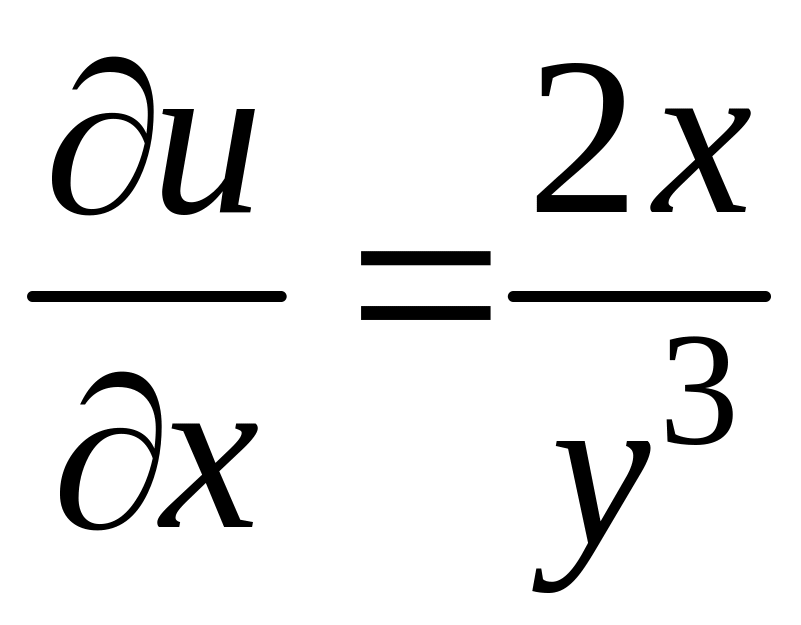 ,
то
,
то
 ,
где
– не определенная пока функция от y.
,
где
– не определенная пока функция от y.
Дифференцируя это
соотношение по y
и учитывая, что
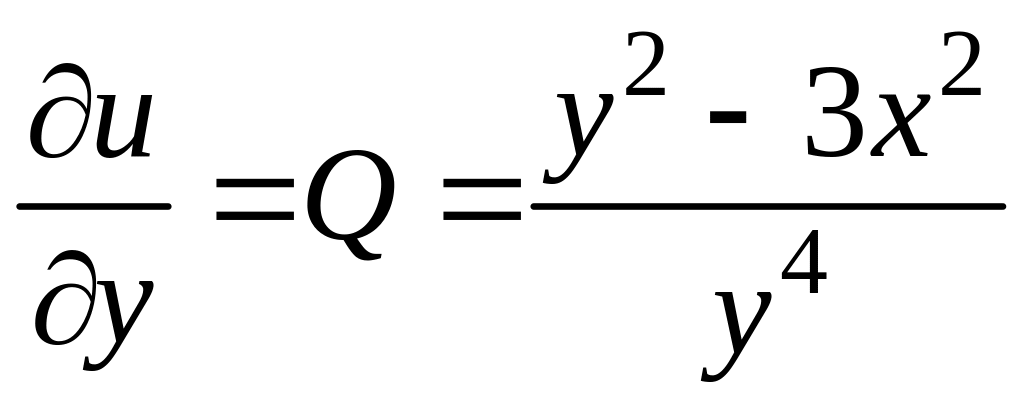 ,
получаем
,
получаем

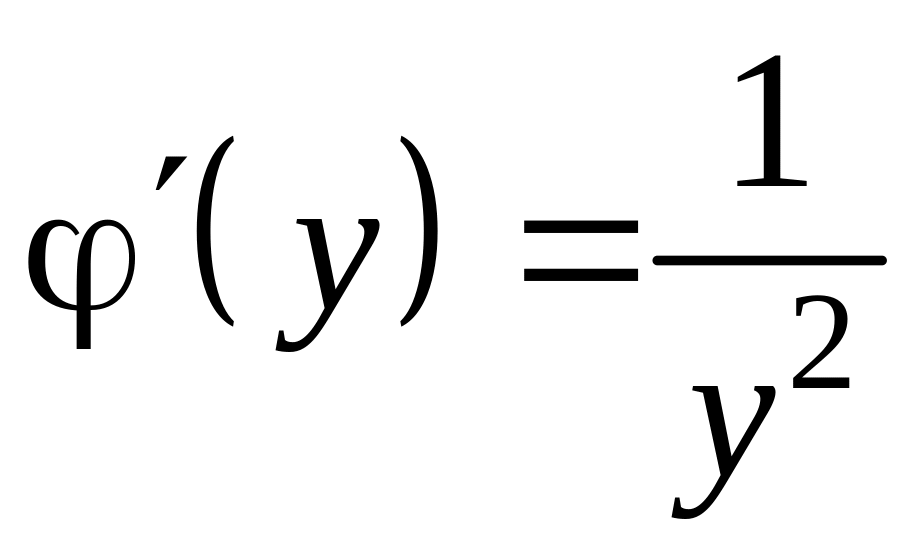
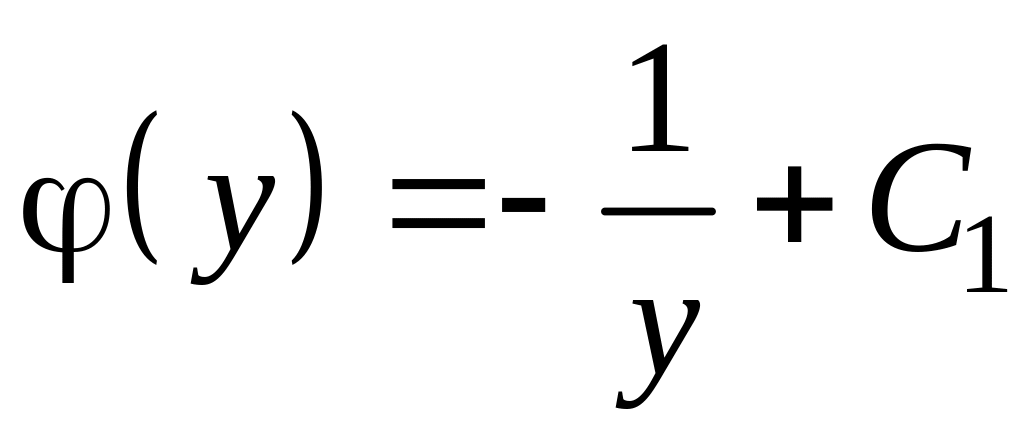 .
Следовательно
.
Следовательно
 .
.
Таким образом, общий интеграл исходного уравнения
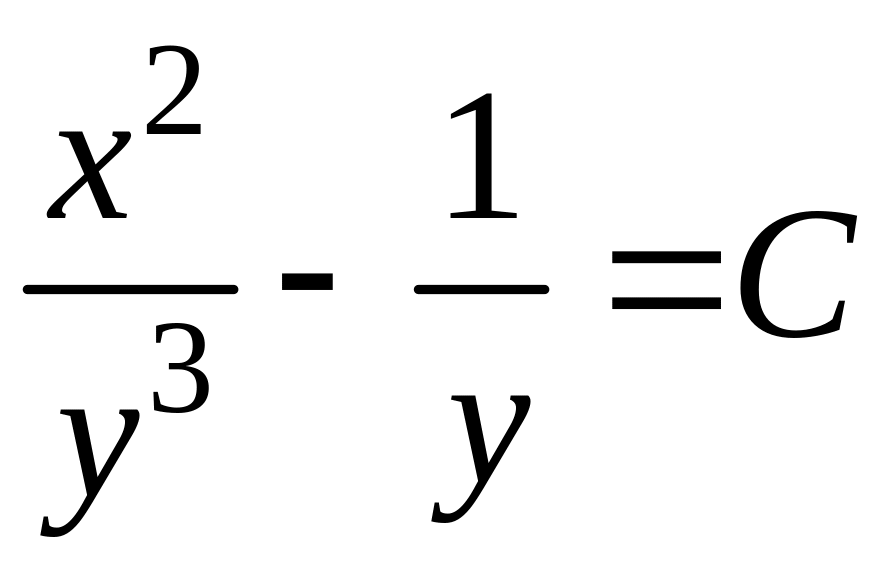 .
.
Замечание. Неизвестную функцию можно сразу находить по одной из формул или .
Пример
9.8.2. Дано
уравнение
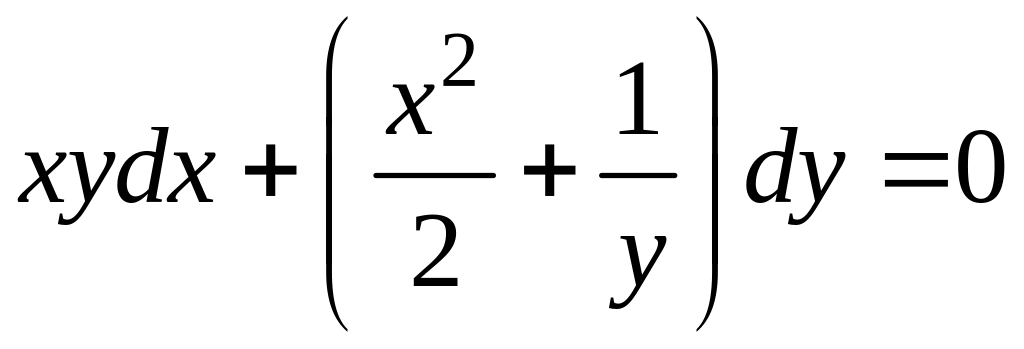
![]() .
.
Решение. Условие
выполнено. Применим формулу , положив
![]() ,
,
![]() .
Получим
.
Получим

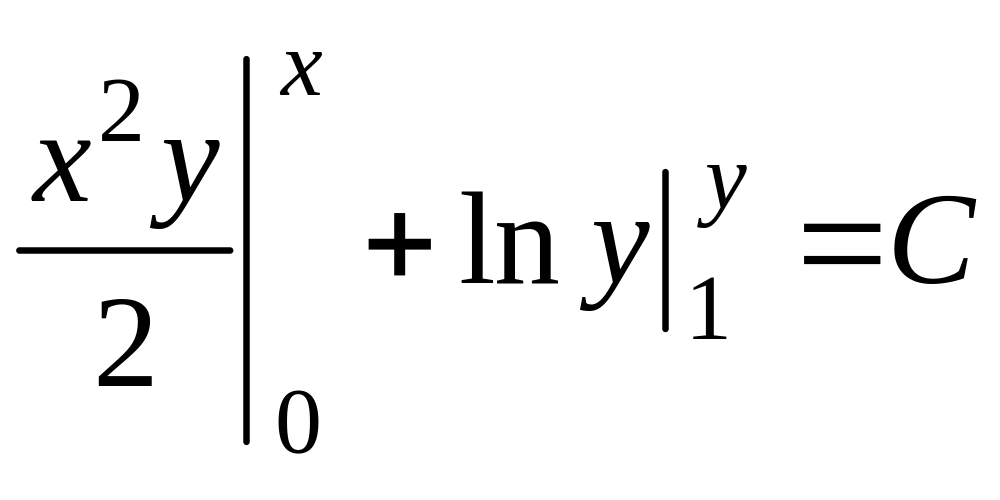
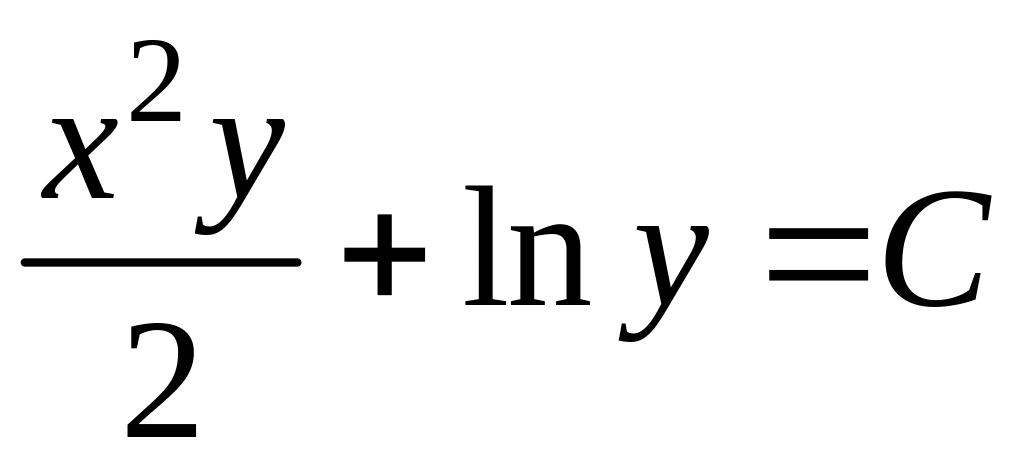 – общий интеграл. Нельзя полагать
– общий интеграл. Нельзя полагать
![]() ,
так как y
= 0 не
принадлежит области определения
коэффициентов.
,
так как y
= 0 не
принадлежит области определения
коэффициентов.
Если
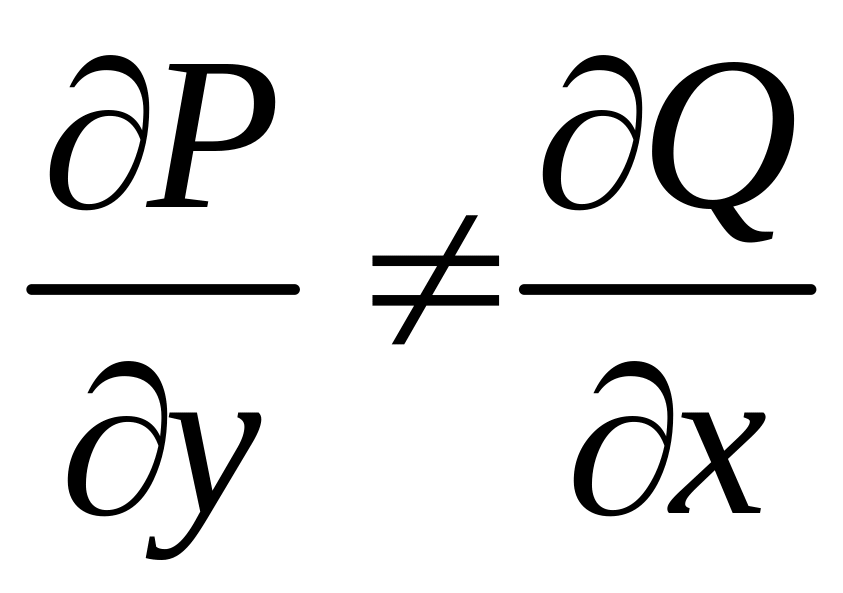 ,
то уравнение
,
то уравнение
![]() уже не является уравнением в полных
дифференциалах. Его можно превратить
в уравнение в полных дифференциалах
умножением обеих частей на подходящим
образом подобранную функцию
уже не является уравнением в полных
дифференциалах. Его можно превратить
в уравнение в полных дифференциалах
умножением обеих частей на подходящим
образом подобранную функцию
![]() ,
которая называется интегрирующим
множителем. В некоторых частных случаях
интегрирующий множитель можно найти.
Более подробно этот вопрос можно найти
в любом учебнике, содержащем дифференциальные
уравнения.
,
которая называется интегрирующим
множителем. В некоторых частных случаях
интегрирующий множитель можно найти.
Более подробно этот вопрос можно найти
в любом учебнике, содержащем дифференциальные
уравнения.
