Контрольная работа № 1

Контрольная работа № 1 состоит из пяти заданий. Ниже подробно рассмотрены варианты решения заданий.

Образец выполнения задания 1

Дано: , , , .

Найти: а) длину ребра ;

б) угол между векторами и ;

в) площадь грани ;

г) объем пирамиды;

д) длину высоты, опущенной из вершины на грань ;

е) длину медианы k к грани .

Решение:

Д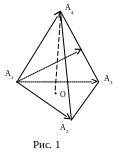 ля наглядности построим пирамиду (необязательно соблюдая масштаб) и отметим на ней используемые векторы (рис. 1).

а) Для вычисления длины ребра найдем координаты вектора . Для этого из координат конца вектора вычтем соответствующие координаты начала :

.

Вычислим длину вектора: .

Ответ: .

k

б) Для вычисления угла между векторами и найдем эти векторы: и .

Воспользуемся формулой .

Скалярное произведение получим как сумму произведений соответствующих координат: .

Вычислим длины векторов и : ; . , .

Ответ: .

в) Площадь грани будем вычислять исходя из геометрического смысла векторного произведения векторов. Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах. Площадь треугольника равна .

Вычислим векторное произведение разложением определителя по первой строке:

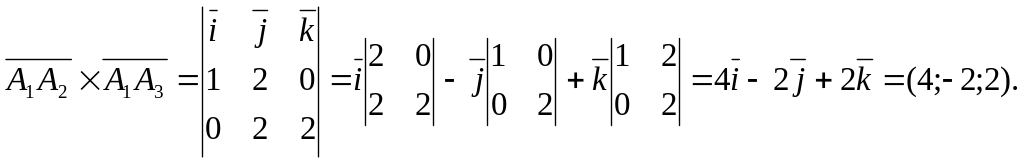
Найдем длину вектора :

Тогда площадь грани равна .

Ответ:

г) Объем пирамиды численно равен модуля смешанного произведения векторов, образующих данную пирамиду, например векторов , , .

, .

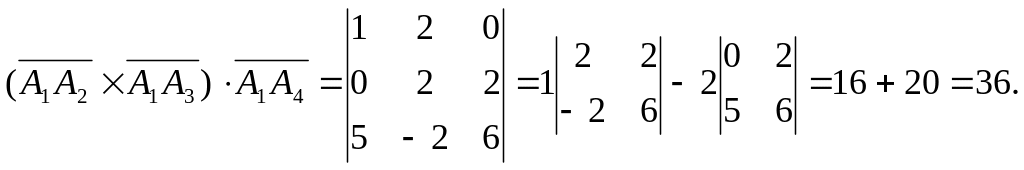
Ответ:

д) Для вычисления высоты, опущенной из вершины на грань , воспользуемся формулой , где - длина высоты пирамиды. Объем пирамиды равен , площадь основания . Тогда , отсюда .

Ответ:

е) Вектор соединяет с серединой стороны . Найдем . Для этого вычислим полусуммы соответствующих координат векторов , , значит, Тогда длина медианы

Ответ:

Образец выполнения задания 2

Составить уравнение линии, каждая точка которой отстоит от точки втрое дальше, чем от прямой . Сделать чертеж.

Дано: точка ; прямая на плоскости .

Решение: Пусть точка лежит на искомой линии. Из проведем две прямые: прямую и прямую , перпендикулярную к прямой . По условию задачи .

Так как , , то

Т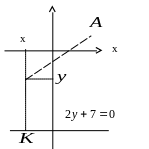 ак как (рис. 2), то Подставим эти значения в (1). Это и есть уравнение линии. Но его можно упростить.

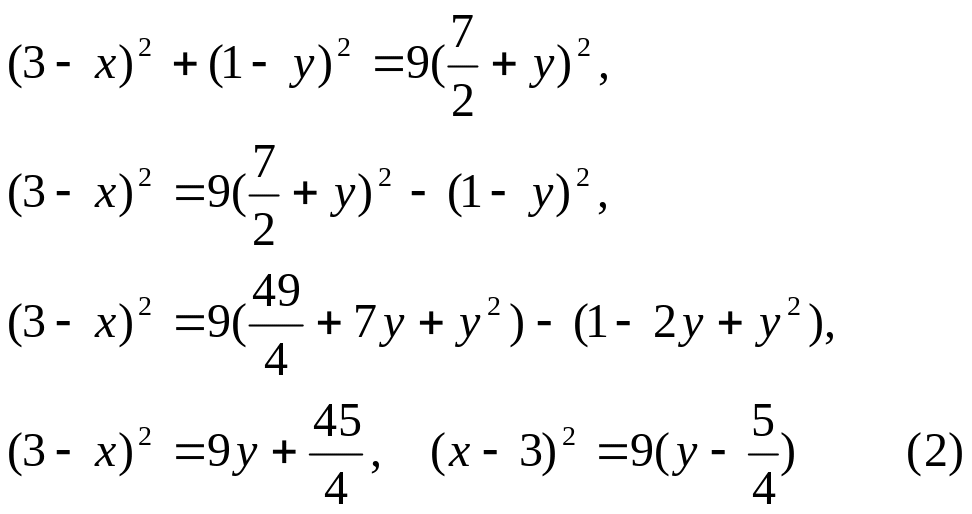
Рис. 2

С делаем замену , . Уравнение примет вид . В системе координат это уравнение изображается параболой (рис. 3). Относительно этой системы координат точка О (начало старой системы координат) имеет координаты . Эти числа взяты из .

Рис. 3

Образец выполнения задания 3

Дано уравнение линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, давая значения через промежуток, равный , начиная от в промежутке ; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.

1. Для построения кривой, заданной уравнением , придаем 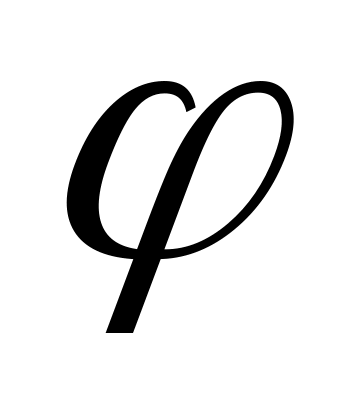значения от до 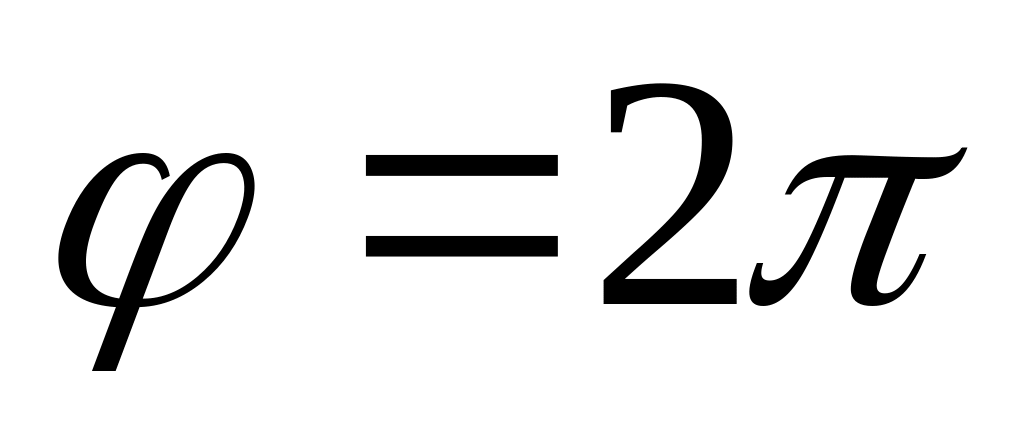через промежуток (с шагом) и заносим полученные значения в таблицу:

2) В полярной системе координат соединяем последовательно точки с координатами , получаем кривую (рис. 4)

3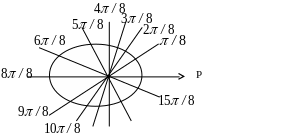 ) Для получения уравнения линии в прямоугольной системе координат подставим значения полярного радиуса и угла , связывающие полярную и прямоугольную системы координат.

Рис. 4

, , .

Тогда .

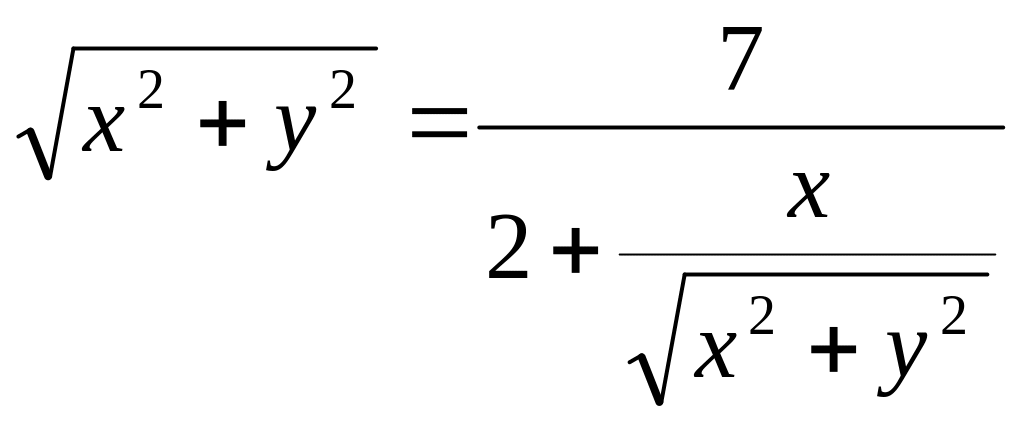
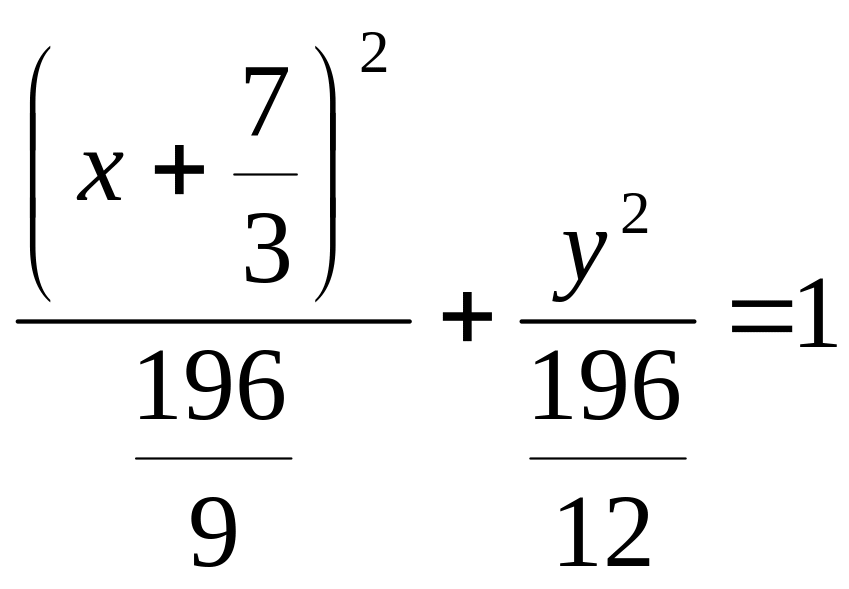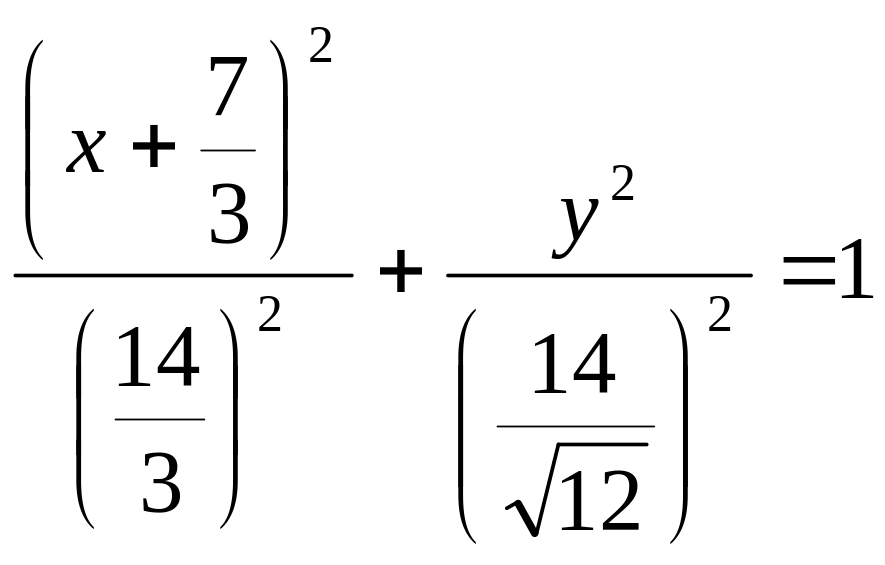- уравнение параболы со смещенным центром .

Напомним, что полярный радиус точки может принимать только неотрицательные значения.

Образец выполнения задания № 4

Дано уравнение прямой и точки . Требуется найти уравнение плоскости, проходящей через точку А и содержащей прямую .

.

Решение:

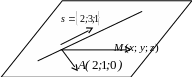
Прямая проходит через точку направляющий вектор . Искомая плоскость проходит через прямую и точку .

Для написания уравнения плоскости рассмотрим текущую точку . Векторы , , компланарны. Следовательно, смешанное произведение этих векторов равно нулю.

,

,

,

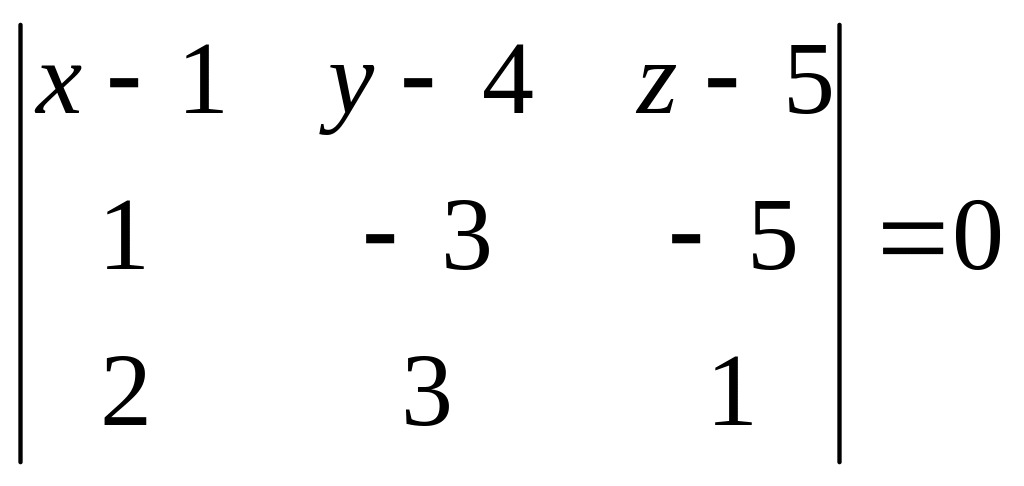
- уравнение плоскости.

Ответ:

Образец выполнения задания № 5

Решить системы линейных алгебраических уравнений методом Гаусса и по формулам Крамера.

а) Дана система линейных уравнений

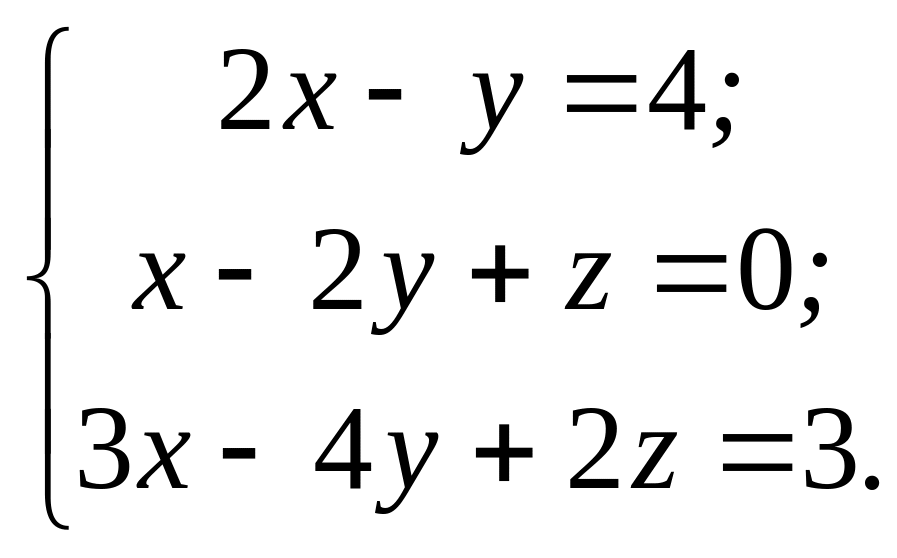
Решить систему двумя способами: 1) Методом Гаусса, 2) по формулам Крамера.

Решение:

а) У данной неоднородной системы число уравнений равно числу неизвестных. Вычислим определитель этой системы:

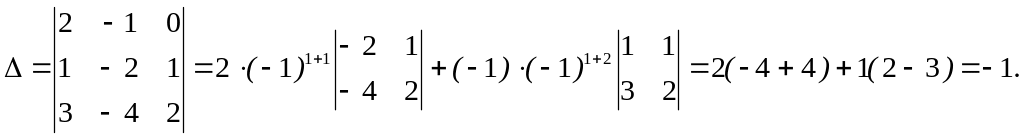
Определитель системы не равен нулю, так что можно применить правило Крамера. Составим вспомогательный определитель , заменив столбец коэффициентов при столбцом свободных членов:

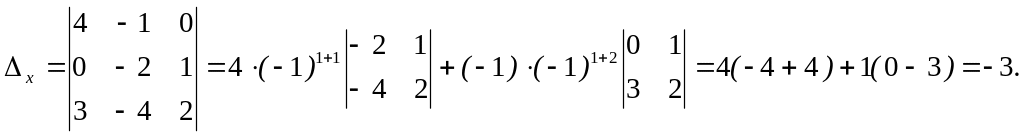
Вычислим определитель , полученный из основного заменой столбца коэффициентов при переменной столбцом свободных членов:

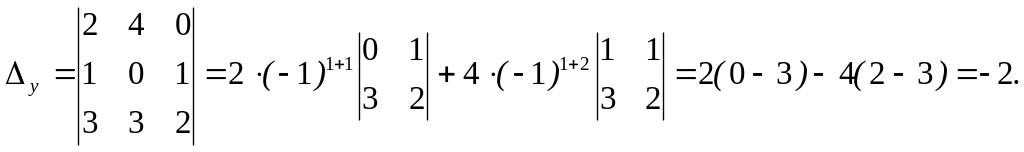
Аналогично вычислим :

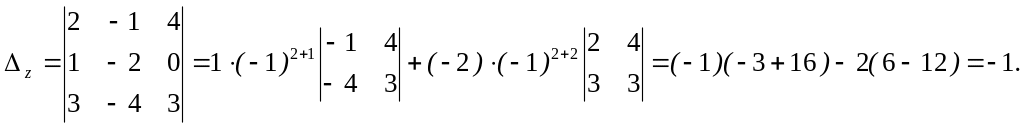
По правилу Крамера: Таким образом,

Ответ: