
Контрольная работа № 2
Контрольная работа № 2 состоит из пяти задач. Ниже подробно рассмотрены варианты решения заданий.
Образец выполнения задания № 6
Найти пределы функций.
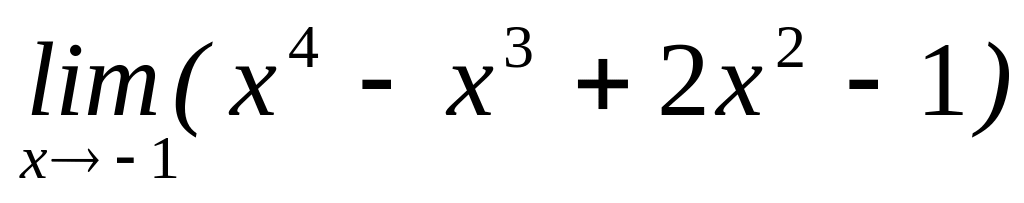 .
.
Решение:
Так как заданная функция непрерывная
(при всех значениях
,
в том числе и при
![]() ),
то предел функции в
равен значению функции в этой точке,
т.е.
),
то предел функции в
равен значению функции в этой точке,
т.е.
![]() .
.
Итак,
![]() .
.
2)
![]() .
.
Решение:
Функция
![]() в предельной точке
в предельной точке
![]() не определена. Она представляет собой
отношение двух бесконечно малых функций
при
не определена. Она представляет собой
отношение двух бесконечно малых функций
при
![]() (неопределенность вида
(неопределенность вида
![]() );
преобразуем ее, чтобы сократить на
множитель, стремящийся к нулю. Разлагаем
знаменатель на множители и сокращаем
дробь на
);
преобразуем ее, чтобы сократить на
множитель, стремящийся к нулю. Разлагаем
знаменатель на множители и сокращаем
дробь на
![]() .
Получаем
.
Получаем
![]() .
.
3)
![]() .
.
Решение:
Функция
![]() в предельной точке
в предельной точке
![]() не определена. Она представляет собой
отношение двух бесконечно малых функций
при
не определена. Она представляет собой
отношение двух бесконечно малых функций
при
![]() (неопределенность вида
).
Разлагаем числитель и знаменатель дроби
на множители, затем, сокращая дробь на
(неопределенность вида
).
Разлагаем числитель и знаменатель дроби
на множители, затем, сокращая дробь на
![]() ,
получаем
,
получаем
![]() .
.
4)
![]() .
.
Решение:
Функция
![]() при
при
![]() представляет собой неопределенность
вида
представляет собой неопределенность
вида
![]() .
Разделив числитель и знаменатель дроби
на
.
Разделив числитель и знаменатель дроби
на
![]() - наивысшую степень
,
находим
- наивысшую степень
,
находим
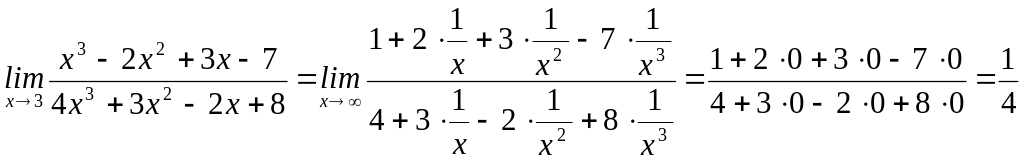 ,
,
так
как при
величины
![]() и
и
![]() являются бесконечно малыми.
являются бесконечно малыми.
5)
![]() .
.
Решение:
Функция
![]() при
при
![]() представляет собой неопределенность
вида
представляет собой неопределенность
вида
![]() .
Рассматривая данную функцию как дробную,
со знаменателем, равным единице, избавимся
от иррациональности в числителе и затем
разделим числитель и знаменатель дроби
на
.
Получаем
.
Рассматривая данную функцию как дробную,
со знаменателем, равным единице, избавимся
от иррациональности в числителе и затем
разделим числитель и знаменатель дроби
на
.
Получаем
![]()
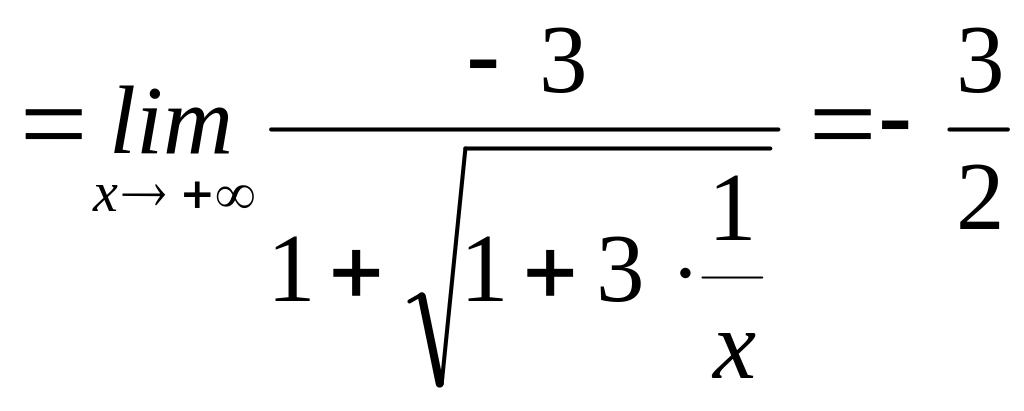 .
.
6)
![]() .
.
Решение:
Функция
![]() в предельной точке
в предельной точке
![]() не определена, она представляет собой
отношение двух бесконечно малых функций
при
не определена, она представляет собой
отношение двух бесконечно малых функций
при
![]() (неопределенность вида
).
(неопределенность вида
).
Применяя
тригонометрическую формулу
![]() и используя первый замечательный предел,
находим
и используя первый замечательный предел,
находим
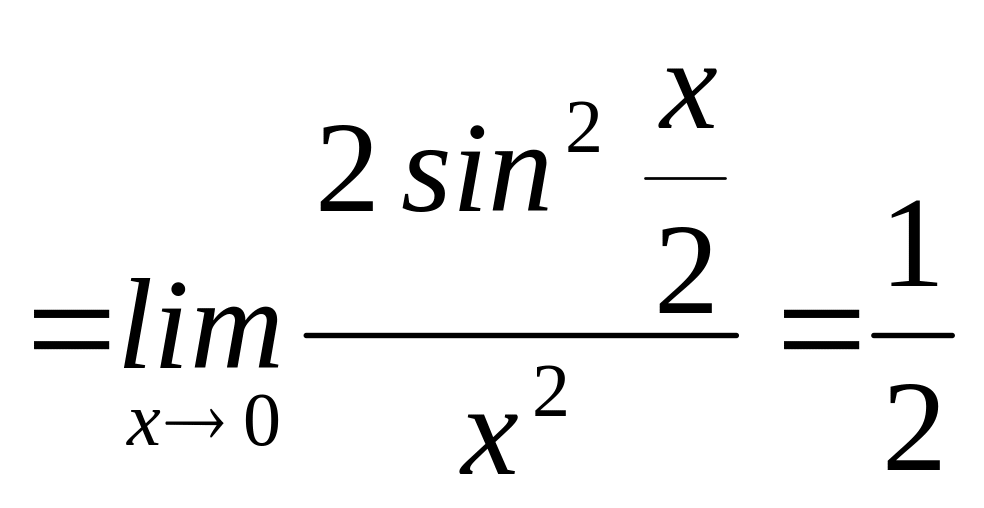
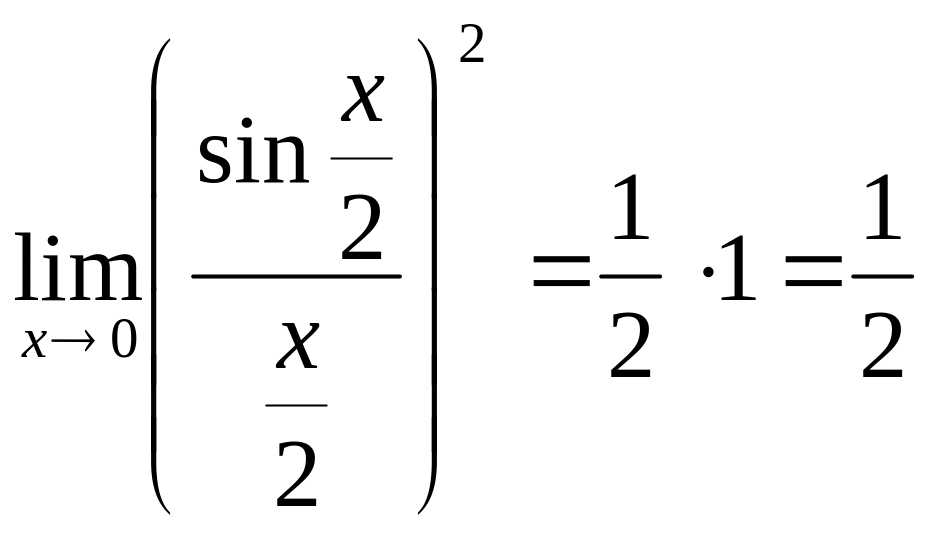 .
.
7)
![]() .
.
Решение:
Функция
![]() в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность вида
).
Преобразуя функцию
в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность вида
).
Преобразуя функцию
![]() и используя первый замечательный предел,
находим
и используя первый замечательный предел,
находим
![]()
![]() .
.
8)
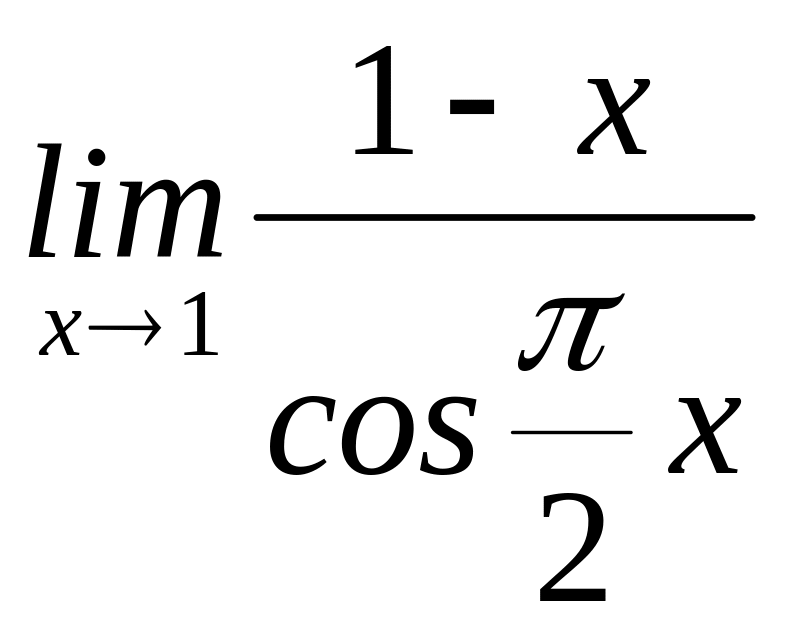 .
.
Решение:
Функция
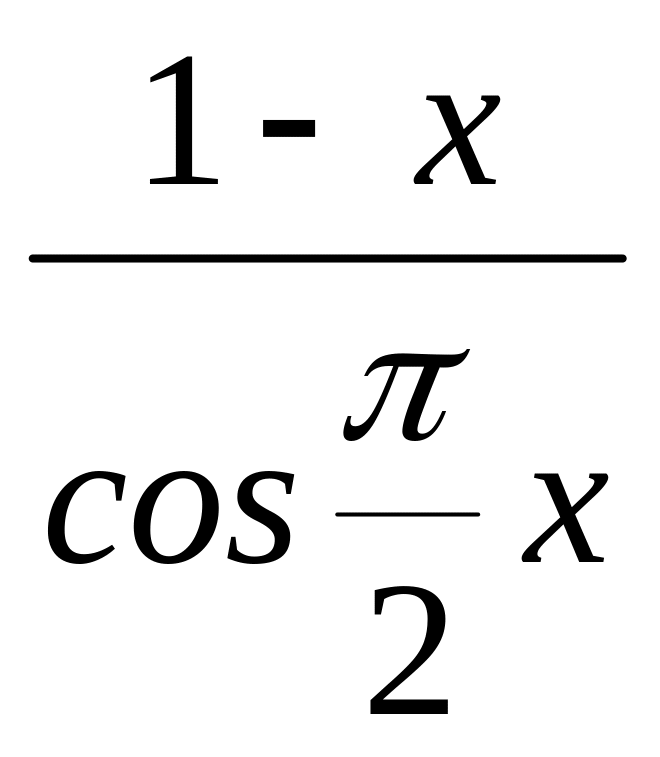 в предельной точке
в предельной точке
![]() не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной,
положив
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной,
положив
![]() .
Тогда при
.
Тогда при
![]() будет
будет
![]() и
и

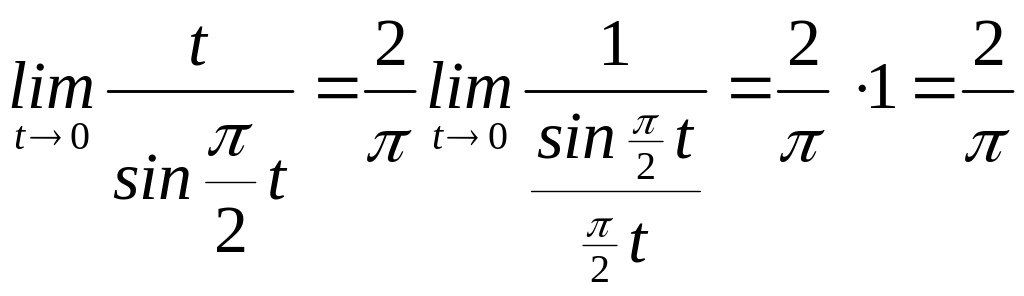 .
.
9)
![]() .
.
Решение:
Функция
![]() в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Преобразуя функцию
в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Преобразуя функцию
![]() и используя первый замечательный предел,
находим
и используя первый замечательный предел,
находим
![]()
![]() .
.
10)
![]() .
.
Решение:
Функция
![]() в предельной точке
в предельной точке
![]() не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной
![]() .
Находим
.
Находим
![]()
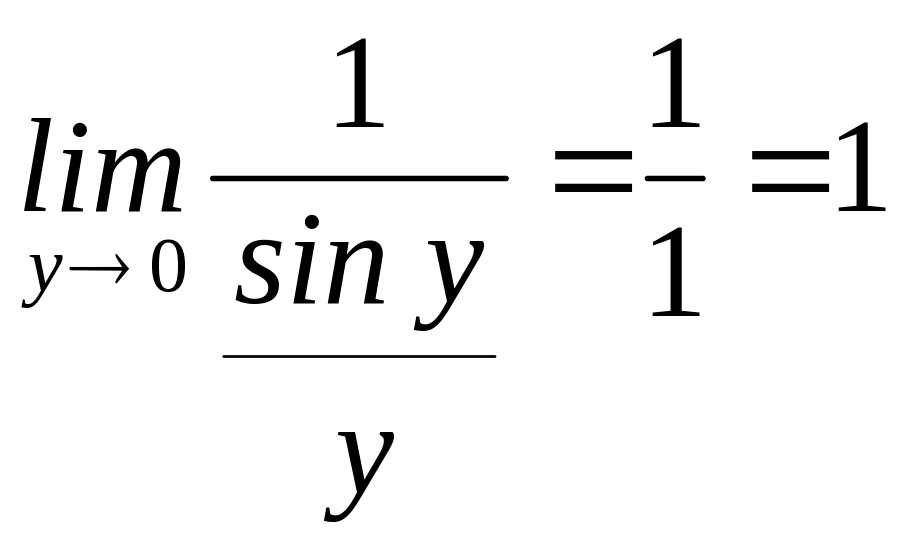 .
.
11)
![]() .
.
Решение:
Функция
![]() в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной
в предельной точке
не определена, она представляет собой
отношение двух бесконечно малых функций
при
(неопределенность
).
Чтобы использовать первый замечательный
предел, сделаем замену переменной
![]() .
Находим
.
Находим
![]()
![]()
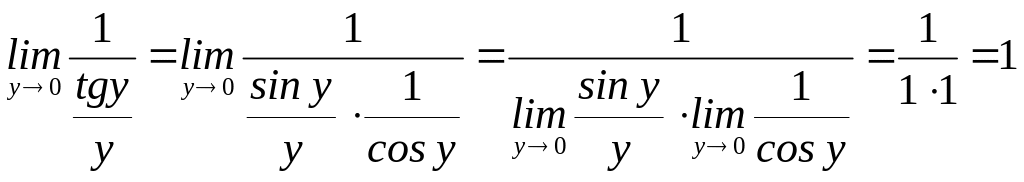 .
.
12)
![]()
![]() .
.
Решение:
Функция
![]() представляет собой отношение двух
бесконечно малых функций при
(неопределенность
).
Преобразуем ее и воспользуемся вторым
замечательным пределом
представляет собой отношение двух
бесконечно малых функций при
(неопределенность
).
Преобразуем ее и воспользуемся вторым
замечательным пределом
![]() .
.
Число
- иррациональное,
![]() Получаем
Получаем
![]() .
.
Таким
образом,
![]() .
.
13)
![]() .
.
Решение:
Делением числителя дроби на знаменатель
выделим целую часть
![]() .
.
Таким образом,
![]()
![]()
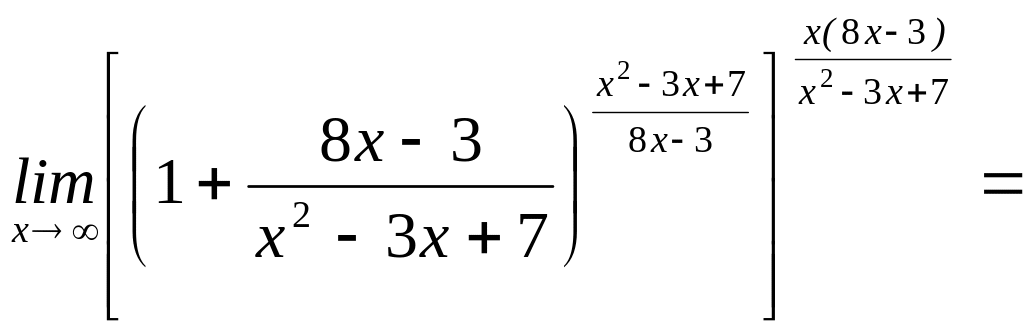
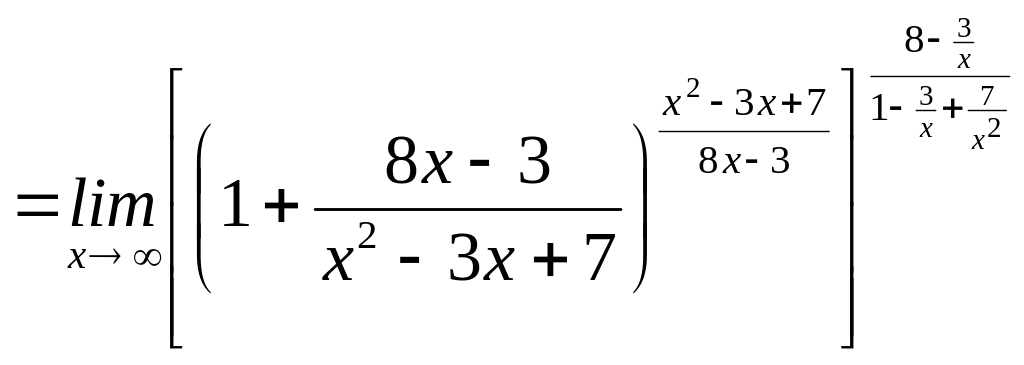 ;
;
так как
![]() при
,
при
,
то
![]()
Приняв
во внимание, что
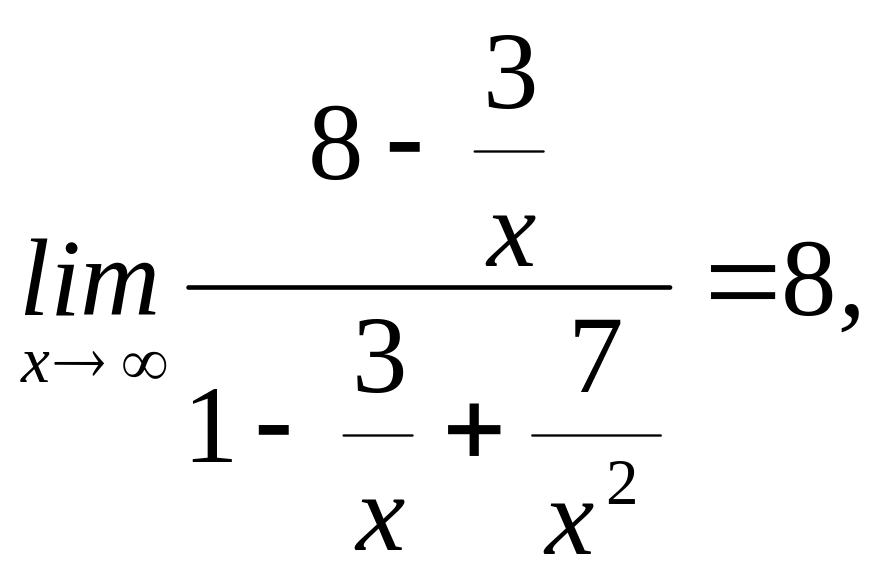 получаем, что
получаем, что
![]() .
.
Образец выполнения задания № 7
а)
Дана функция
![]() и значения аргумента
и значения аргумента
![]() ,
,
![]() .
1) Определить пределы функции при
приближении к
,
слева и справа. 2) Установить, является
ли данная функция непрерывной или
разрывной. 3) Сделать схематический
чертеж.
.
1) Определить пределы функции при
приближении к
,
слева и справа. 2) Установить, является
ли данная функция непрерывной или
разрывной. 3) Сделать схематический
чертеж.
Решение:
1) Исследуем на непрерывность в точке
![]() .
По определению: функция
.
По определению: функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
если
,
если
![]() .
.
Определим предел
слева:
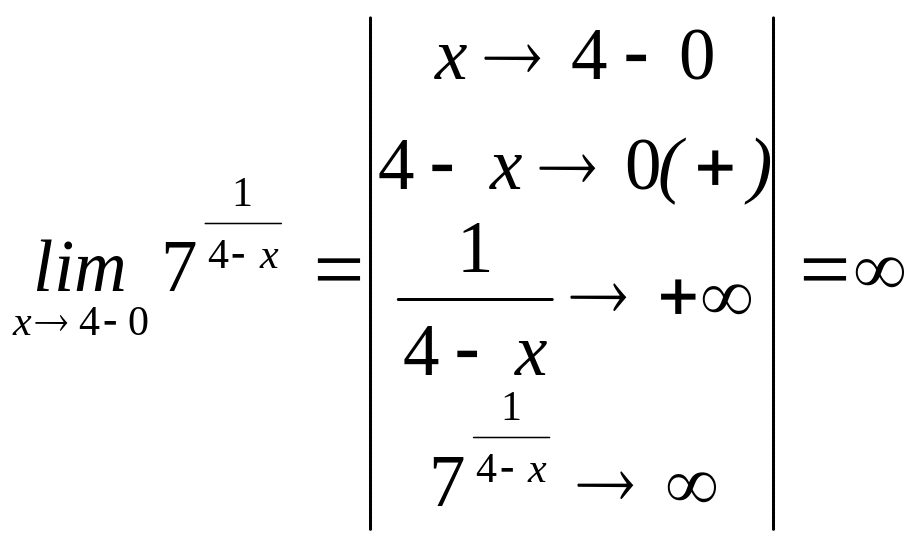 .
.
Определим
предел справа:
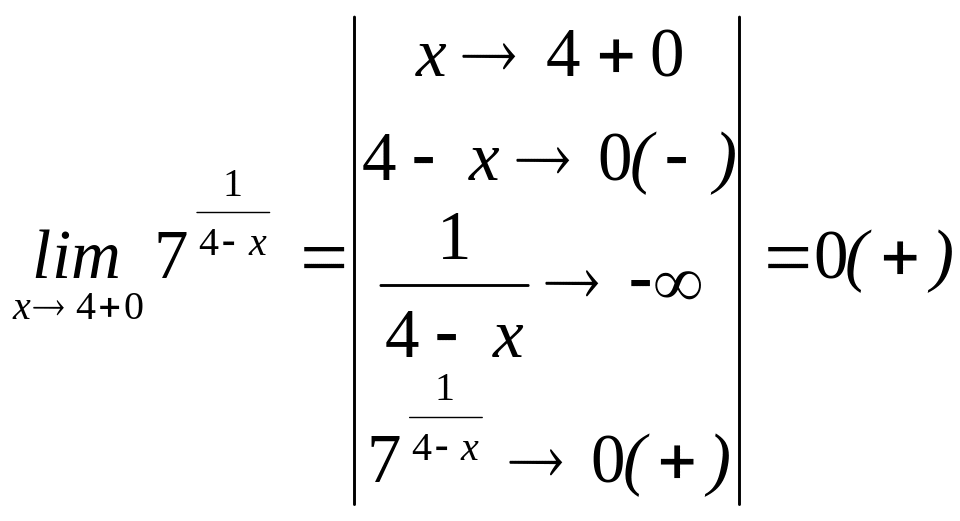 .
.
![]() функция
терпит разрыв в точке
второго рода.
функция
терпит разрыв в точке
второго рода.
Исследуем на непрерывность в точке .
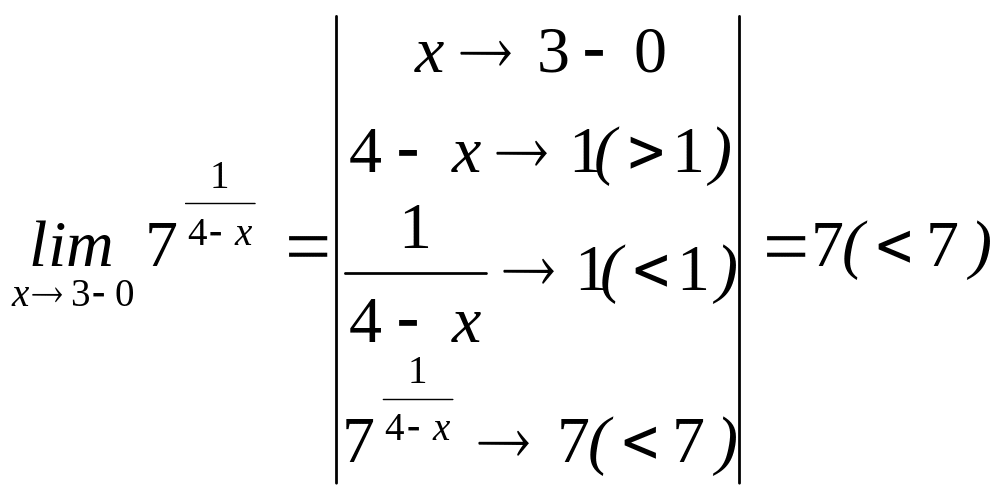 ;
;
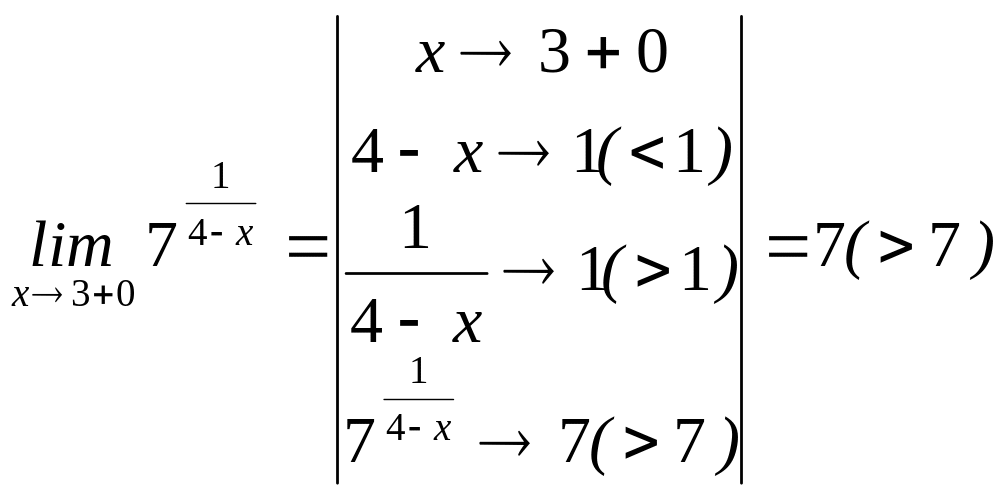 .
.
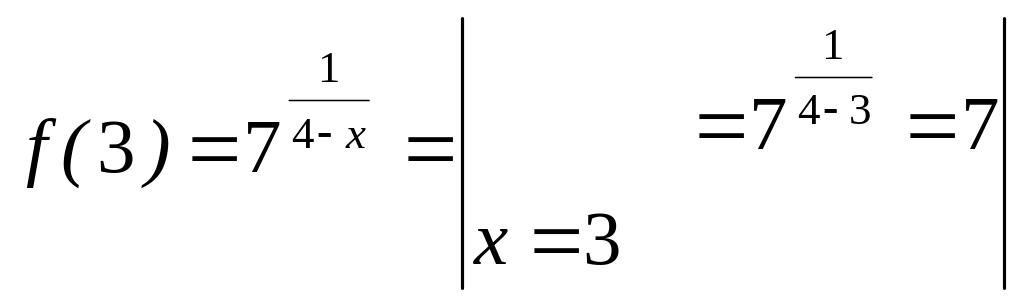 ,
,
![]()
![]() в точке
непрерывна.
в точке
непрерывна.
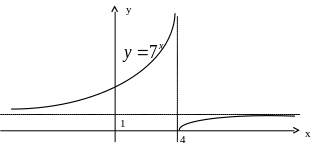
Рис. 5
Образец выполнения задания № 8
Применяя формулы и правила дифференцирования, найти производные следующих функций.
Решение:
Перепишем заданную функцию в виде
![]()
![]()
2)
![]()
Решение:
![]()
3)
![]()
Решение:
Обозначим
![]() ;
тогда
;
тогда
![]() .
По правилу дифференцирования сложной
функции имеем
.
По правилу дифференцирования сложной
функции имеем
![]() .
.
4)
![]() .
.
Решение:
![]() .
.
5)
![]() .
.
Решение:
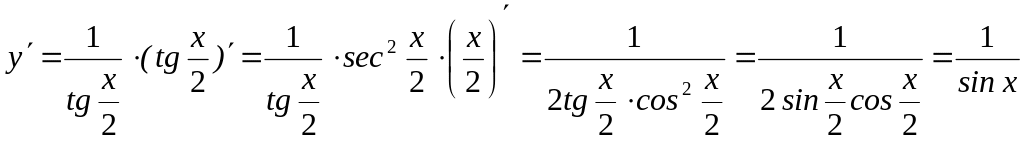 .
.
6)
![]() .
.
Решение:
![]()
![]()
![]() .
.
7)
![]() .
.
Решение: Здесь основание и показатель степени зависят от . Логарифмируя, получим
![]() .
.
Дифференцируем
обе части последнего равенства по
.
Так как
является функцией
,
то
![]() есть сложная функция
и
есть сложная функция
и
![]() .
.
Следовательно,
![]() ,
,
![]() ,
,
![]() .
.
Образец выполнения заданий № 10
На какой высоте
надо повесить фонарь над центром круговой
площади радиуса
![]() ,
чтобы площадка была максимально освещена
у ее границы?
,
чтобы площадка была максимально освещена
у ее границы?
Из курса физики
известно, что освещенность
![]() обратно пропорциональна квадрату
расстояния от источника света и прямо
пропорциональна косинусу угла падения
(угла, образованного нормально к
поверхности с направлением светового
потока), т.е.
обратно пропорциональна квадрату
расстояния от источника света и прямо
пропорциональна косинусу угла падения
(угла, образованного нормально к
поверхности с направлением светового
потока), т.е.
![]() ,
где k зависит от силы
источника света, помещенного в точке А
(рис. 6). Из треугольника ОАВ имеем
,
где k зависит от силы
источника света, помещенного в точке А
(рис. 6). Из треугольника ОАВ имеем
![]() и
и
![]() .
Приняв h за независимую
переменную, получим
.
Приняв h за независимую
переменную, получим
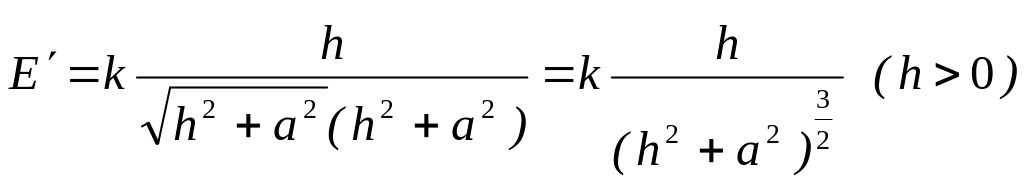 .
.
Исследуем функцию на экстремум с помощью первой производной:
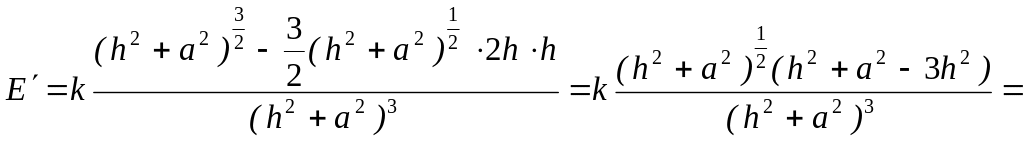
 ;
;
![]() при
при
![]() .
.
Т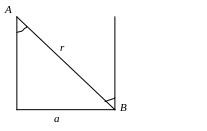 ак
как
ак
как
![]() в промежутке
в промежутке
![]() и
и
![]() в промежутке
в промежутке
![]() ,
то при
функция имеет максимум, т.е. при значении
,
то при
функция имеет максимум, т.е. при значении
![]() освещенность в точке В является
наибольшей.
освещенность в точке В является
наибольшей.
Рис. 6
