
- •Введение
- •Выводы по графику
- •Вывод по ответу
- •Интерференция света Краткие теоретические сведения Природа света
- •Сложение световых волн. Интерференция
- •Сложение колебаний одного направления и одинаковой частоты. Условия наблюдения интерференционных максимумов и минимумов
- •Условия наблюдения интерференции света
- •Расчет интерференционной картины от двух источников
- •Методы наблюдения интерференции
- •Интерференция в тонких пленках
- •Полосы равного наклона
- •Полосы равной толщины
- •Расчет ширины интерференционной полосы от угла клина
- •Интерферометры
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы и задания
- •Дифракция света Краткие теоретические сведения
- •Принцип Гюйгенса.
- •Метод зон Френеля
- •Дифракция Френеля на круглом отверстии
- •Дифракция Фраунгофера на круглом отверстии
- •Дифракция Фраунгофера на одной щели
- •Дифракция Фраунгофера на дифракционной решетке
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы и задания
- •Поляризация света Краткие теоретические сведения Естественный и поляризованный свет
- •Способы получения поляризованного света
- •Закон Малюса
- •Закон Брюстера
- •Анализ поляризованного света
- •Лабораторная работа № 7 проверка закона малюса
- •Описание лабораторной установки
- •Порядок выполнения работы
- •Контрольные вопросы и задания
- •Библиографический список
Полосы равного наклона
В случае падения сходящегося или расходящегося пучка света на плоскопараллельную пластинку (пленку) при интерференции возникают полосы равного наклона. При наблюдении интерференционной картины используют собирающую линзу ( ) и экран.
Схема
возникновения полос равного наклона
приведена на рис. 1.9. Лучи, падающие на
пластинку под определенным углом
(луч
и параллельные ему), соберутся на экране
в одной точке
.
Лучи, падающие на пластинку под другим
углом (например, луч
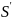 ),
собираются в другой точке экрана
),
собираются в другой точке экрана
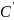 .
.
Если имеется протяженный источник света, то под тем же углом будет падать много лучей, поэтому на экране получится не одна точка , а семейство точек, т. е. будет наблюдаться интерференционная полоса равного наклона. Интерференционная картина на экране будет иметь вид чередующихся светлых и темных полос, каждой из которых соответствует определенное значение угла падения . При освещении пластинки белым светом на экране возникает система разноцветных полос равного наклона. Если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона имеют вид чередующихся концентрических темных и светлых колец.

В отсутствии линзы лучи уходят в бесконечность. В этом случае говорят, что полосы равного наклона локализованы в бесконечности. Это явление используется на практике для контроля степени параллельности тонких пленок (пластин). Изменение толщины пленки на 108 м можно обнаружить по искажению формы полос равного наклона.
Полосы равной толщины
Несколько другая интерференционная картина наблюдается при освещении светом тонких пленок с переменной толщиной (плоский клин).
Рассмотрим
лучи 1
и 2,
падающие на поверхность клина с малым
углом раствора
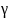 ,
приведенные на рис. 1.10.
,
приведенные на рис. 1.10.
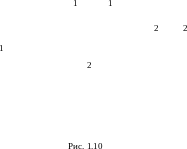
В месте падения, в соответствии с законами
отражения и преломления света, часть
света отразится, а часть, преломившись,
отразится от нижней поверхности, далее
преломится на верхней поверхности
пленки и пересечется с отраженным лучом.
При этом будут наблюдаться интерференционные
полосы, параллельные ребру клина,
называемые полосами
равной толщины.
Если свет падает на пленку нормально,
то полосы равной толщины локализуются
на верхней поверхности клина.
месте падения, в соответствии с законами
отражения и преломления света, часть
света отразится, а часть, преломившись,
отразится от нижней поверхности, далее
преломится на верхней поверхности
пленки и пересечется с отраженным лучом.
При этом будут наблюдаться интерференционные
полосы, параллельные ребру клина,
называемые полосами
равной толщины.
Если свет падает на пленку нормально,
то полосы равной толщины локализуются
на верхней поверхности клина.
Кольца Ньютона – это кольцевые полосы равной толщины, наблюдаемые при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой (рис. 1.11).
Параллельный пучок света падает нормально (перпендикулярно) на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При нормальном падении света возникают полосы равной толщины, имеющие вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. В центре находится темное пятно (минимум), окруженное системой концентрических светлых и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центра.
В
отраженном свете оптическая разность
хода (с учетом потери полуволны при
отражении), согласно (1.6), при условии,
что показатель преломления воздуха
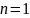 ,
а угол падения
,
а угол падения
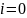 ,
,
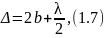
где – толщина воздушного зазора.
Согласно
теореме Пифагора, для треугольника
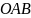 (рис. 1.11)
(рис. 1.11)
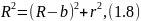
где
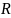 – радиус
кривизны линзы;
– радиус
кривизны линзы;
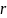 – радиус
окружности, всем точкам которой
соответствует одинаковый зазор
.
– радиус
окружности, всем точкам которой
соответствует одинаковый зазор
.
Из формулы (1.8) следует
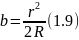
при
условии
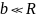 .
.
Подставим выражение (1.8) в (1.6). Тогда
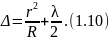
Приравняв (1.10) к условиям максимумов (1.2) и минимумов (1.3), получим выражения для радиуса -го светлого кольца
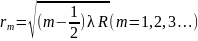
и для радиуса -го темного кольца
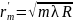
 .
.
Кольца
Ньютона можно наблюдать и в проходящем
свете, причем
в этом случае максимумам
интерференции в отраженном свете будут
соответствовать минимумы в проходящем
свете и наоборот, поскольку не происходит
потери полуволны при отражении света
от оптически менее плотной среды для
обоих отраженных лучей и разность хода
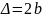 .
.
