Пример 3. Найти область определения функции .

Решение. Для существования функции необходимо, чтобы . Для существования функции надо, чтобы , откуда . Для существования функции необходимо, чтобы , откуда и .

Таким образом, получены условия

.

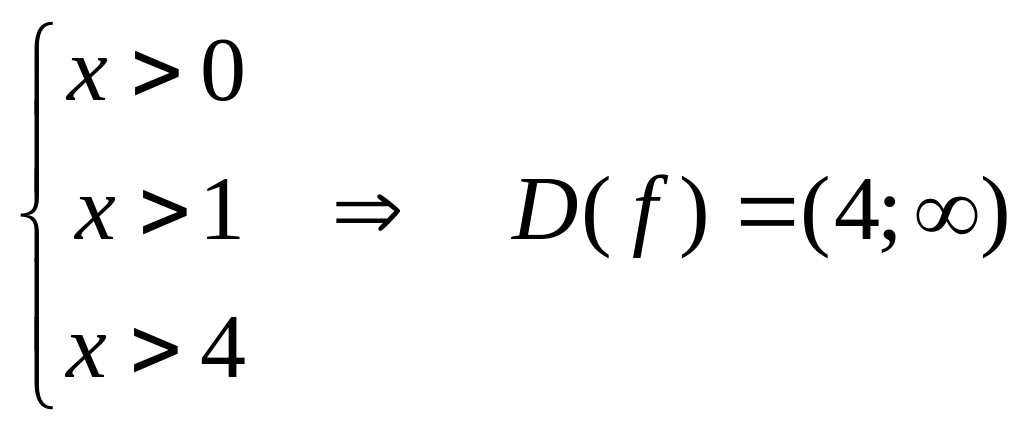Пример 4. Найти область определения функции

.

Решение. Так как , то

.

Решив неравенство, найдем область определения функции

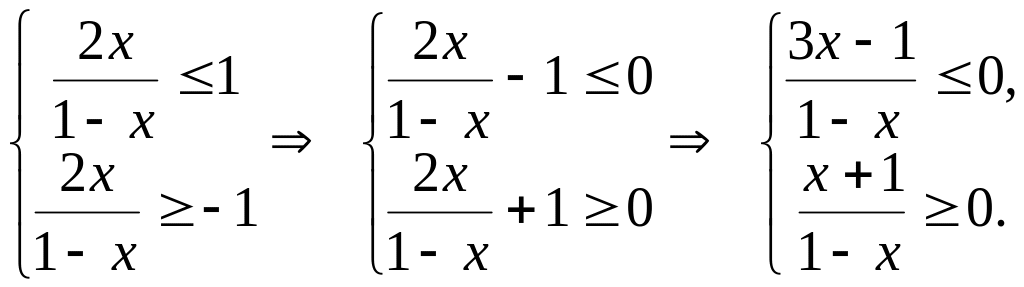
Применим метод интервалов (рис. 1.1)

1.
^1/3 1	.
2.
^-1 1	.
Рис. 1.1.

Система неравенств имеет решение .

Следовательно, .

Пример 5. Определить, являются ли функции

1. ;

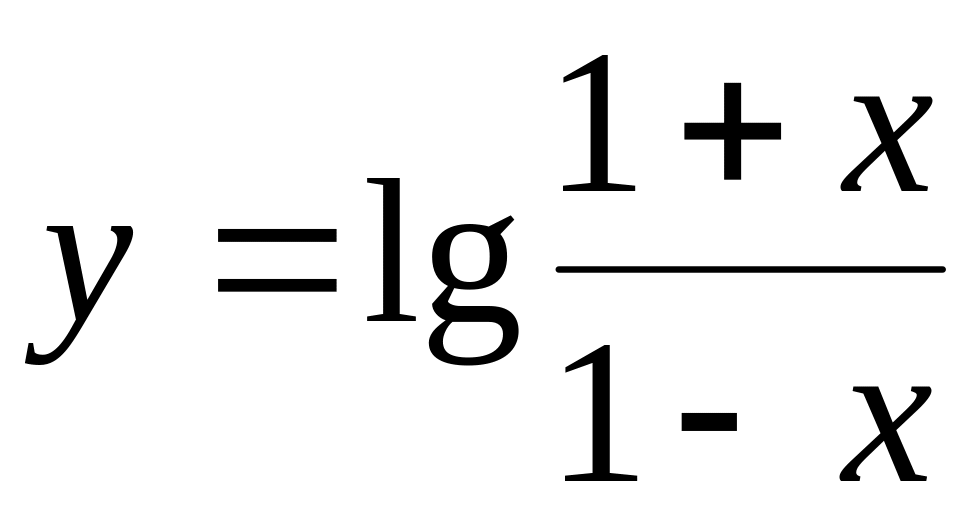2. 2. ;

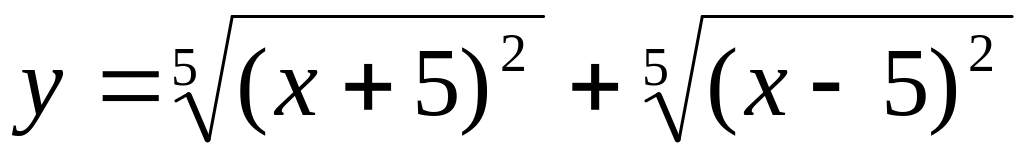3. ;

4.

четными или нечетными.

Решение. Для определения свойств четности или нечетности функции следует проверить выполнение следующих положений:

1. Является ли область определение симметричной относительно начала координат, т.е. если , то и ;

3. Выполняются ли равенства 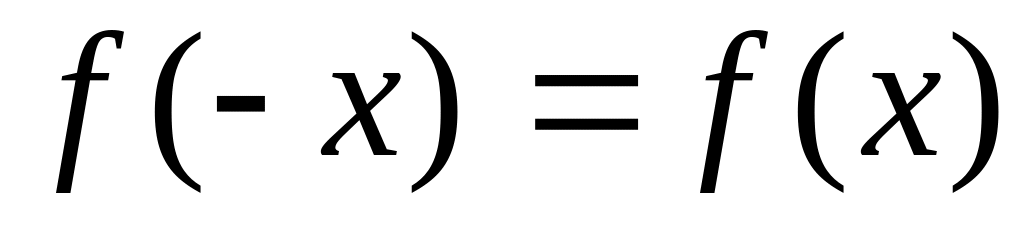или 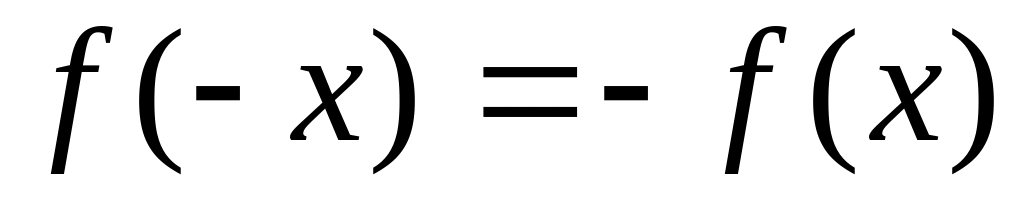. При выполнении первого равенства функция окажется четной с графиком, симметричным относительно оси ординат, во втором – нечетной с графиком, симметричным относительно начала координат.

Для указанных в задаче функций:

1. ,

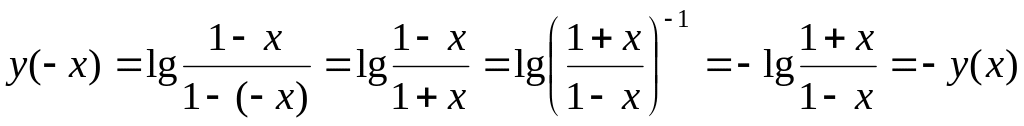то функция - нечетная;

2. ,

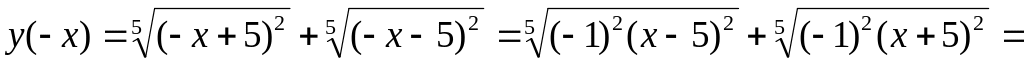
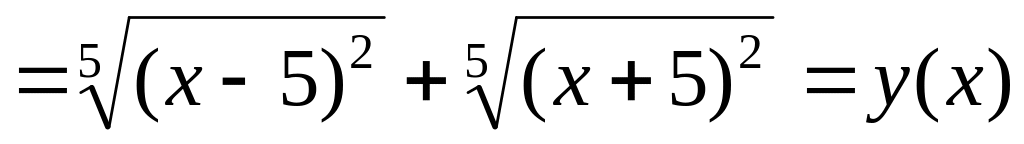то функция является четной;

3. ,

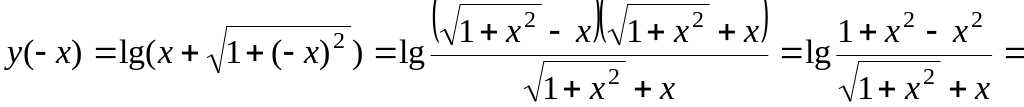
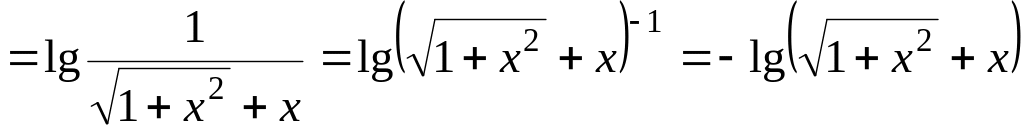следовательно, функция нечетная;

4. ,

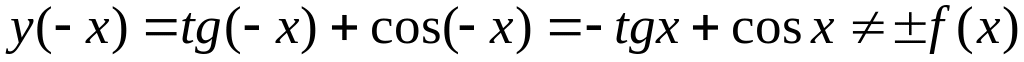следовательно, функция не является ни четной, ни нечетной.

Пример 6. Найти период функции .

Решение.

Так как , то период Т=1.

Глава 2. Определение предела функции. Определение бесконечно малой и бесконечно большой величины.

-окрестностью точки A называется отрезок (A-, A+). Аналогично δ - окрестностью точки х₀ называется отрезок (х₀ - δ, х₀ + δ).

Предел функции

Пусть на некотором отрезке задана функция f(x). Число A называется пределом функции y = f (x) при xx₀ (при х стремящемся к х₀), если для каждого сколь угодно малого числа  > 0 можно указать зависящее от  положительное число () > 0 такое, что для всех х, удовлетворяющих неравенству x₀ - х<  (т.е. лежащих в δ – окрестности точки х₀), имеет место неравенство A – f (x) < . Запись

или . (2.1)

Наличие у функции f(x) предела A в точке х₀ означает, что как только независимая переменная х достаточно близко приблизится к значению х₀, то функция f(x) будет сколь угодно близка к A.

Пример. Доказать, что .

Решение. Зададим произвольное и покажем, что существует положительное такое, что из неравенства вытекает неравенство .

Действительно

.

Значит, если положить , то выполнение неравенства влечет за собой выполнение неравенства . Таким образом, согласно определению, заключаем, что

Если при хx₀ функция f(x) стремится к 0, то ее называют бесконечно малой функцией или бесконечно малой величиной (или просто бесконечно малой) в окрестности точки x₀. Бесконечно малые обозначают греческими буквами , , .

Тем самым для бесконечно малой функции для каждого сколь угодно малого числа  > 0 можно указать зависящее от  положительное число () > 0 такое, что для всех х, удовлетворяющих неравенству x₀ - х< , имеет место неравенство  α(х)  < . Запись

. (2.2)

Примеры бесконечно малых величин:

(х) = 2x - 6 при х  3,

(х) = e^-x при х  ,

(х) = sin x при х  0 и т.п.

Бесконечно малые величины часто обозначают символом «0».

Для бесконечно малых функций справедливы следующие утверждения:

1. Сумма бесконечно малых величин есть величина бесконечно малая

α(х) + β (х) = γ(х).

2. Произведение бесконечно малых величин есть величина бесконечно малая

α(х) β (х) = γ(х).

3. Произведение бесконечно малой на число есть величина бесконечно малая

С α(х) = γ(х).

4. Функция называется ограниченной на своей области определения D, если существует такое положительное число М, что

 f(x) < М

для всех х D. Произведение бесконечно величины малой на ограниченную функцию есть величина бесконечно малая.

α(х) f(x) = γ(х).

Функция f(x) называется бесконечно большой функцией или бесконечно большой величиной при х сстремящемся к х₀, если для любого сколь угодно большого числа М можно указать зависящее от М число (М) > 0 такое, что для всех х, удовлетворяющих неравенству x₀ -х< , имеет место неравенство f (x) > М. Запись

.

К бесконечно большим относятся, например:

y = 1/x при х  0,

y = lg (x) при х   и при х  + 0 и др.

Замечание. Бесконечность (обозначаемая знаком ) не является числом.

Для бесконечно больших функций справедливы следующие утверждения:

1. Сумма бесконечно больших величин, имеющих один знак, есть величина бесконечно большая.

2. Произведение бесконечно больших величин есть величина бесконечно большая.

3. Произведение бесконечно большой на число есть величина бесконечно большая.

Между бесконечно малой и бесконечно большой величинами существует простое соотношение: если α(х) - бесконечно малая величина не равная тождественно нулю в окрестности точки х₀, то f(x) = 1/α(х) - бесконечно большая величина в окрестности точки х₀ и наоборот. Символьная запись этого утверждения

.

Действительно, из определения бесконечно малой следует, что для каждого сколь угодно малого числа  > 0 можно указать зависящее от  положительное число () > 0 такое, что для всех х, удовлетворяющих неравенству x₀ - х< , имеет место неравенство  α(х)  < . Тогда для f(x) = 1/α(х) выполняется соотношение

.

А это и означает, что f(x) бесконечно большая величина при xx₀.

Аналогично доказывается что величина обратная бесконечно большой есть бесконечно малая.

Поэтому, если 2 х - 6 является бесконечно малой величиной в окрестности точки х = 3, то 1/(2х-6) - бесконечно большая в окрестности той же точки. Так как 1/х бесконечно большая в окрестности точко ноль, то х есть бесконечно малая в окрестности той же точки.