
- •Раздел 3.
- •Глава 1. Функции. Основные определения.
- •Пример 3. Найти область определения функции .
- •Глава 2. Определение предела функции. Определение бесконечно малой и бесконечно большой величины.
- •Предел функции
- •Глава 3. Правила вычисления пределов функции.
- •Пример 3. Вычислить .
- •Глава 4. Предельные переходы в неравенствах. Замечательные пределы.
- •Пример 4. Вычислить .
- •Глава 5. Непрерывность функции. Односторонние пределы.
Пример 4. Вычислить .
Решение. Так
как
![]() ,
а
,
а
![]() ,
то имеет место неопределенность вида
,
то имеет место неопределенность вида
![]() .
.
Выполним преобразования
![]()
![]() .
.
Пример 5.
Вычислить
![]() .
.
Решение. Так
как
![]() и
и
![]() ,
то имеет место неопределенность вида
,
то имеет место неопределенность вида
![]() .
.
Возможны 2 способа решения примера.
1-й способ. Вспомним,
что есть замечательный предел
![]() .
.
Используем этот замечательный предел, преобразовав исходный предел следующим образом:
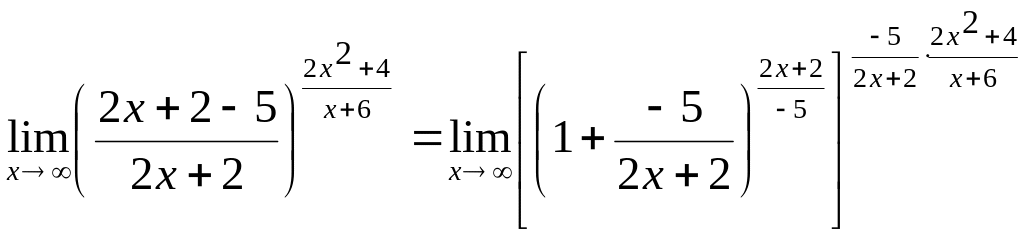 .
.
Имеем
![]() (здесь
(здесь
![]() ),
),
и
![]() .
.
Таким образом,
![]() .
.
2-й способ.
![]()
![]()
![]() .
.
.
Причем
![]() при
при
![]() .
Выразим
.
Выразим
![]() из равенства
из равенства
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
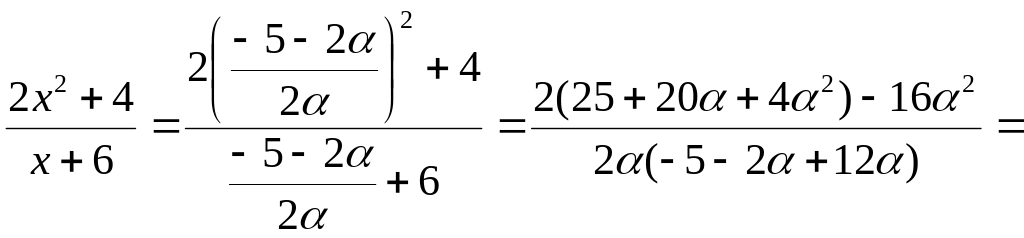
![]() .
.
Выполним замену
![]() .
.
Так как
![]() ,
а
,
а
![]() ,
,
то в итоге предел
равен
![]() .
.
Глава 5. Непрерывность функции. Односторонние пределы.
Функция f(x) называется непрерывной в точке х0, если она определена в этой точке и некоторой ее окрестности, а также
![]() (5.1)
(5.1)
Точки, в которых равенство (5.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка.
Обозначим за х разность между двумя значениями аргумента х = х2 –х1, а за f (x) разность между двумя значениями функции f(x) = f(x2) - f(x1). Тогда, если функция непрерывна, то бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если х 0, то и f (x) 0.
Введем понятие односторонних пределов. Число А называется пределом функции f(x) слева, если хx0 оставаясь все время меньше х0 (x < x0). Запись предела слева
![]()
Аналогично вводится понятие предела справа, в этом случае хx0 оставаясь все время больше х0 (x > x0). Запись предела справа
![]()
Для непрерывной функции предел слева совпадает с пределом справа и равен значению функции в точке х0
![]() =
=![]() =
f(x0).
=
f(x0).
В точках разрыва цепочка равенств нарушается. Разрыв называется «разрывом первого рода», если все пределы конечны и «разрывом второго рода», если хотя бы один из пределов не существует или бесконечен.
Если хотя бы один из пределов равен бесконечности в точке х = х0 , то говорят, что в этой точке есть вертикальная асимптота. Функция, имеющая на конечном промежутке конечное число разрывов первого рода называется кусочно непрерывной.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
Пример 1. Найти точки разрыва функции.
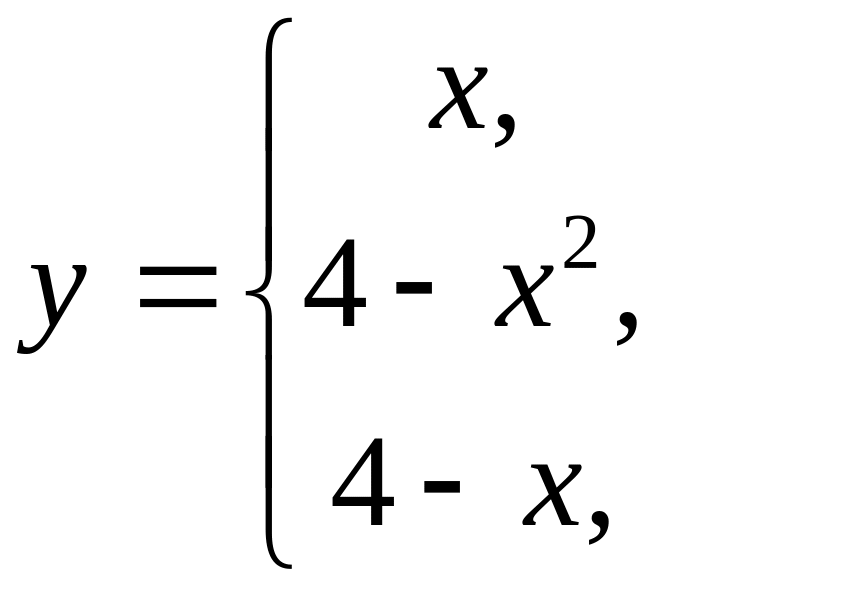 если
если
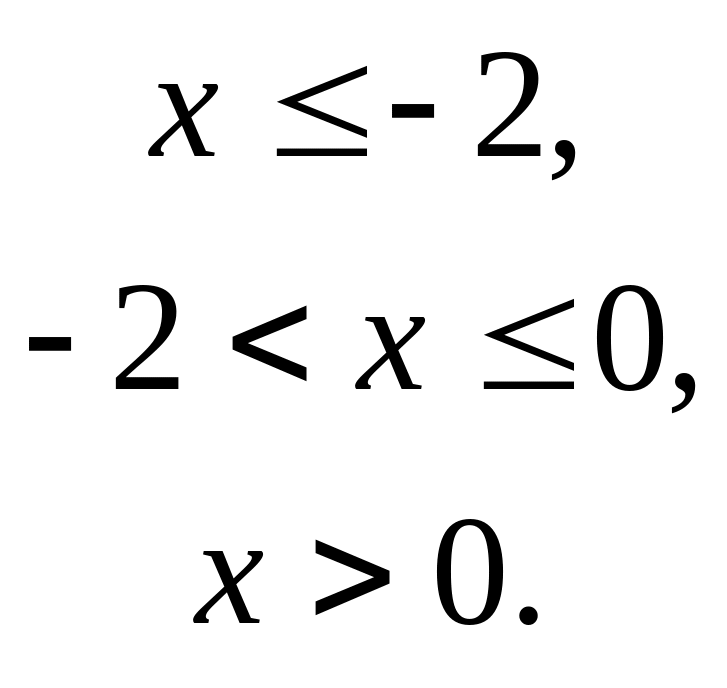
Решение. На
интервалах
![]() ,
,
![]() и
и
![]() функция непрерывна. Проверке подлежат
только точки
функция непрерывна. Проверке подлежат
только точки
![]() и
и
![]() .
.
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Рассмотрим точку .
![]() .
.
Вычислим односторонние пределы
![]() ,
,
![]() .
.
Так как односторонние пределы не совпадают, - точка разрыва функции.
Рассмотрим точку .
![]() ,
,
![]() ,
,
![]() ,
,
![]() - точка непрерывности
функции, выполнены все условия
непрерывности (рис. 5.1).
- точка непрерывности
функции, выполнены все условия
непрерывности (рис. 5.1).
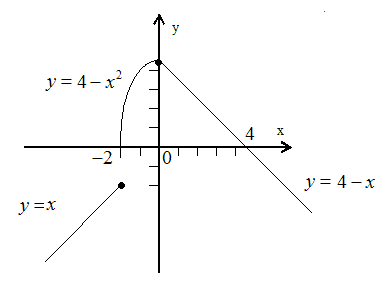
Рис. 5.1.
Пример 2.
Исследовать поведение функции
![]() вблизи точки разрыва. Построить
схематический чертеж.
вблизи точки разрыва. Построить
схематический чертеж.
Решение.
Область определения функции
![]()
Точка разрыва
![]() .
Найдем односторонние пределы
.
Найдем односторонние пределы
![]() ;
;
![]() .
.
Знак предела
зависит от знаков числителя и
знаменателя дроби. В обоих случаях
числитель
![]() ,
но знаменатель в пределе слева
остается отрицательным, приближаясь
к нулю, а в пределе справа, приближаясь
к нулю, знаменатель остается
положительным. Схематичный чертеж
представлен на рис. 5.2.
,
но знаменатель в пределе слева
остается отрицательным, приближаясь
к нулю, а в пределе справа, приближаясь
к нулю, знаменатель остается
положительным. Схематичный чертеж
представлен на рис. 5.2.
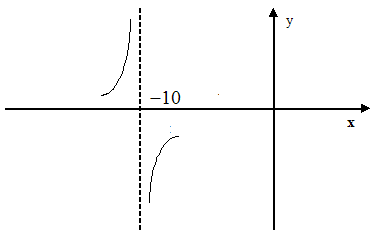
Рис. 5.2.
